ezyang’s blog

New to this series? Start at the beginning!.

Today we’re going to take a closer look at a somewhat unusual data type, Omega. In the process, we’ll discuss how the lub library works and how you might go about using it. This is of practical interest to lazy programmers, because lub is a great way to modularize laziness, in Conal’s words.

Omega is a lot like the natural numbers, but instead of an explicit Z (zero) constructor, we use bottom instead. Unsurprisingly, this makes the theory easier, but the practice harder (but not too much harder, thanks to Conal’s lub library). We’ll show how to implement addition, multiplication and factorial on this data type, and also show how to prove that subtraction and equality (even to vertical booleans) are uncomputable.

This is a literate Haskell post. Since not all methods of the type classes we want to implement are computable, we turn off missing method warnings:

> {-# OPTIONS -fno-warn-missing-methods #-}

Some preliminaries:

> module Omega where
>
> import Data.Lub (HasLub(lub), flatLub)
> import Data.Glb (HasGlb(glb), flatGlb)

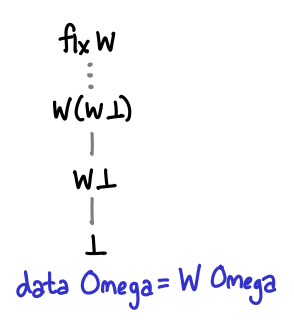
Here is, once again, the definition of Omega, as well as two distinguished elements of it, zero and omega (infinity.) Zero is bottom; we could have also written undefined or fix id. Omega is the least upper bound of Omega and is an infinite stack of Ws.

> data Omega = W Omega deriving (Show)
>
> zero, w :: Omega
> zero = zero
> w    = W w -- the first ordinal, aka Infinity

Here are two alternate definitions of w:

w = fix W
w = lubs (iterate W zero)

The first alternate definition writes the recursion with an explicit fixpoint, as we’ve seen in the diagram. The second alternate definition directly calculates ω as the least upper bound of the chain [⊥, W ⊥, W (W ⊥) ...] = iterate W ⊥.

What does the lub operator in Data.Lub do? Up until now, we’ve only seen the lub operator used in the context of defining the least upper bound of a chain: can we usefully talk about the lub of two values? Yes: the least upper bound is simply the value that is “on top” of both the values.

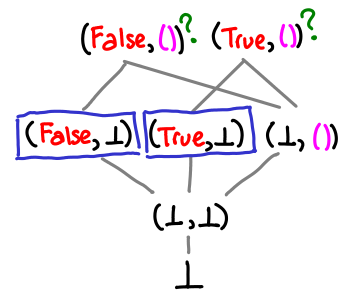
If there is no value on top, the lub is undefined, and the lub operator may give bogus results.

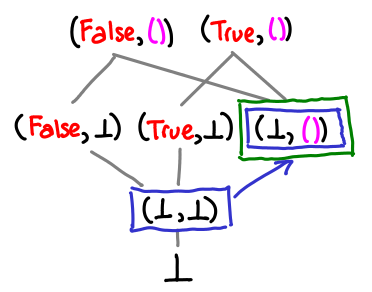
If one value is strictly more defined than another, it may simply be the result of the lub.

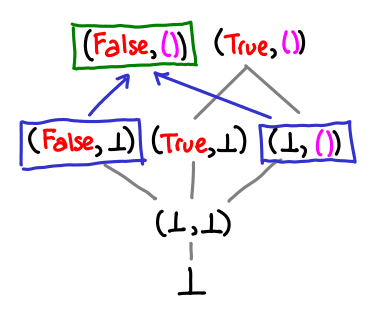
An intuitive way of thinking of the lub operator is that it combines the information content of two expressions. So (1, ⊥) knows about the first element of the pair, and (⊥, 2) knows about the second element, so the lub combines this info to give (1, 2).

How might we calculate the least upper bound? One thing to realize is that in the case of Omega, the least upper bound is in fact the max of the two numbers, since this domain totally ordered.

> instance Ord Omega where
>     max = lub
>     min = glb

Correspondingly, the minimum of two numbers is the greatest lower bound: a value that has less information content than both values.

If we think of a conversation that implements case lub x y of W a -> case a of W _ -> True, it might go something like this:

Me

Lub, please give me your value.

Lub

Just a moment. X and Y, please give me your values.

X

My value is W and another value.

Lub

Ok Edward, my value is W and another value.

Me

Thanks! Lub, what’s your next value?

Lub

Just a moment. X, please give me your next value.

Y

(A little while later.) My value is W and another value.

Lub

Ok. Y, please give me your next value.

Y

My next value is W and another value.

Lub

Ok Edward, my value is W and another value.

Me

Thanks!

X

My value is W and another value.

Lub

Ok.

Here is a timeline of this conversation:

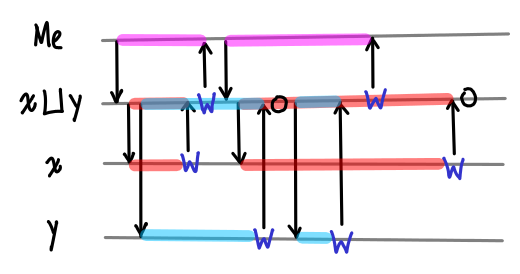
There are a few interesting features of this conversation. The first is that lub itself is lazy: it will start returning answers without knowing what the full answer is. The second is that X and Y “race” to return a particular W, and lub will not act on the result that comes second. However, the ordering doesn’t matter, because the result will always be the same in the end (this will not be the case when the least upper bound is not defined!)

The unamb library that powers lub handles all of this messy, concurrency business for us, exposing it with the flatLub operator, which calculates the least upper bound for a flat data type. We need to give it a little help to calculate it for a non-flat data type (although one wonders if this could not be automatically derivable.)

> instance Enum Omega where
>     succ = W
>     pred (W x) = x -- pred 0 = 0
>     toEnum n = iterate W zero !! n
>
> instance HasLub Omega where
>     lub x y = flatLub x y `seq` W (pred x `lub` pred y)

An equivalent, more verbose but more obviously correct definition is:

isZero (W _) = False -- returns ⊥ if zero (why can’t it return True?)
lub x y = (isZero x `lub` isZero y) `seq` W (pred x `lub` pred y)

It may also be useful to compare this definition to a normal max of natural numbers:

data Nat = Z | S Nat

predNat (S x) = x
predNat Z = Z

maxNat Z Z = Z
maxNat x y = S (maxNat (predNat x) (predNat y))

We can split the definition of lub into two sections: the zero-zero case, and the otherwise case. In maxNat, we pattern match against the two arguments and then return Z. We can’t directly pattern match against bottom, but if we promise to return bottom in the case that the pattern match succeeds (which is the case here), we can use seq to do the pattern match. We use flatLub and lub to do multiple pattern matches: if either value is not bottom, then the result of the lub is non-bottom, and we proceed to the right side of seq.

In the alternate definition, we flatten Omega into Bool, and then use a previously defined lub instance on it (we could have also used flatLub, since Bool is a flat domain.) Why are we allowed to use flatLub on Omega, which is not a flat domain? There are two reasons: the first is that seq only cares about whether or not the its first argument is bottom or not: it implicitly flattens all domains into “bottom or not bottom.” The second reason is that flatLub = unamb, and though unamb requires the values on both sides of it to be equal (so that it can make an unambiguous choice between either one), there is no way to witness the inequality of Omega: both equality and inequality are uncomputable for Omega.

> instance Eq Omega where -- needed for Num

The glb instance rather easy, and we will not dwell on it further. The reader is encouraged to draw the conversation diagram for this instance.

> instance HasGlb Omega where
>    glb (W x') (W y') = W (x' `glb` y')

This is a good point to stop and think about why addition, multiplication and factorial are computable on Omega, but subtraction and equality are not. If you take the game semantics route, you could probably convince yourself pretty well that there’s no plausible conversation that would get the job done for any of the latter cases. Let’s do something a bit more convincing: draw some pictures. We’ll uncurry the binary operators to help the diagrams.

Here is a diagram for addition:

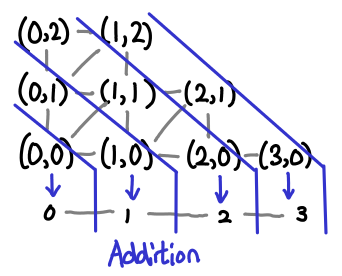
The pairs of Omega form a matrix (as usual, up and right are higher on the partial order), and the blue lines separate sets of inputs into their outputs. Multiplication is similar, albeit a little less pretty (there are a lot more slices).

We can see that this function is monotonic: once we follow the partial order into the next “step” across a blue line, we can never go back.

Consider subtraction now:

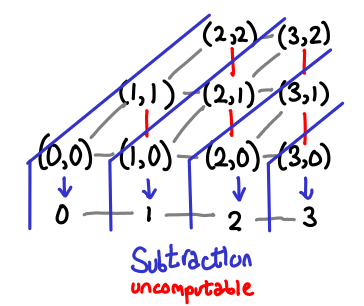
Here, the function is not monotonic: if I move right on the partial order and enter the next step, I can go “backwards” by moving up (the red lines.) Thus, it must not be computable.

Here is the picture for equality. We immediately notice that mapping (⊥, ⊥) to True will mean that every value will have to map to True, so we can’t use normal booleans. However, we can’t use vertical booleans (with ⊥ for False and () for True) either:

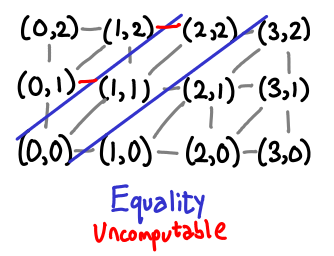
Once again, you can clearly see that this function is not monotonic.

It is now time to actually implement addition and multiplication:

> instance Num Omega where
>     x + y = y `lub` add x y
>         where add (W x') y = succ (x' + y)
>     (W x') * y = (x' * y) + y
>     fromInteger n = toEnum (fromIntegral n)

These functions look remarkably similar to addition and multiplication defined on Peano natural numbers:

natPlus Z y = y
natPlus (S x') y = S (natPlus x' y)

natMul Z y = Z
natMul (S x') y = natPlus y (natMul x' y)

There is the pattern matching on the first zero as before. But natPlus is a bit vexing: we pattern match against zero, but return y: our seq trick won’t work here! However, we can use the observation that add will be bottom if its first argument is bottom to see that if x is zero, then the return value will be y. What if x is not zero? We know that add x y must be greater than or equal to y, so that works as expected as well.

We don’t need this technique for multiplication because zero times any number is zero, and a pattern match will do that automatically for us.

And finally, the tour de force, factorial:

factorial n = W zero `lub` (n * factorial (pred n))

We use the same trick that was used for addition, noting that 0! = 1. For factorial 1, both sides of the lub are in fact equal, and for anything bigger, the right side dominates.

---

To sum up the rules for converting pattern matches against zero into lubs (assuming that the function is computable):

f ⊥ = ⊥
f (C x') = ...

becomes:

f (C x') = ...

(As you may have noticed, this is just the usual strict computation). The more interesting case:

g ⊥ = c
g (C x') = ...

becomes:

g x = c `lub` g' x
  where g' (C x') = ...

assuming that the original function g was computable (in particular, monotonic.) The case where x is ⊥ is trivial; and since ⊥ is at the bottom of the partial order, any possible value for g x where x is not bottom must be greater than or equal to bottom, fulfilling the second case.

---

A piece of frivolity. Quantum bogosort is a sorting algorithm that involves creating universes with all possible permutations of the list, and then destroying all universes for which the list is not sorted.

As it turns out, with lub it’s quite easy to accidentally implement the equivalent of quantum bogosort in your algorithm. I’ll use an early version of my addition algorithm to demonstrate:

x + y = add x y `lub` add y x
  where add (W x') y = succ (x' + y)

Alternatively, (+) = parCommute add where:

parCommute f x y = f x y `lub` f y x

This definition gets the right answer, but needs exponentially many threads to figure it out. Here is a diagram of what is going on:

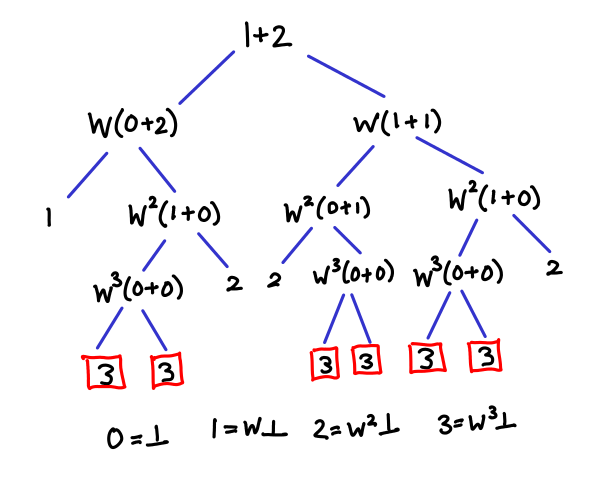
The trick is that we are repeatedly commuting the arguments to addition upon every recursion, and one of the nondeterministic paths leads to the result where both x and y are zero. Any other branch in the tree that terminates “early” will be less than the true result, and thus lub won’t pick it. Exploring all of these branches is, as you might guess, inefficient.

---

Next time, we will look at Scott induction as a method of reasoning about fixpoints like this one, relating it to induction on natural numbers and generalized induction. If I manage to understand coinduction by the next post, there might be a little on that too.