Let’s play a game
Ever wondered how Haskellers are magically able to figure out the implementation of functions just by looking at their type signature? Well, now you can learn this ability too. Let’s play a game.
You are an inventor, world renowned for your ability to make machines that transform things into other things. You are a proposer.

But there are many who would doubt your ability to invent such things. They are the verifiers.

The game we play goes as follows. You, the proposer, make a claim as to some wondrous machine you know how to implement, e.g. (a -> b) -> a -> b (which says given a machine which turns As into Bs, and an A, it can create a B). The verifier doubts your ability to have created such a machine, but being a fair minded skeptic, furnishes you with the inputs to your machine (the assumptions), in hopes that you can produce the goal.
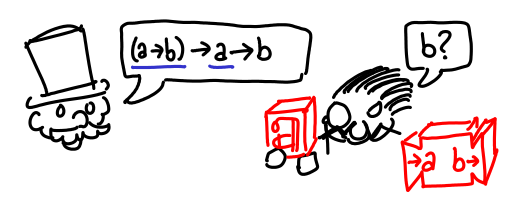
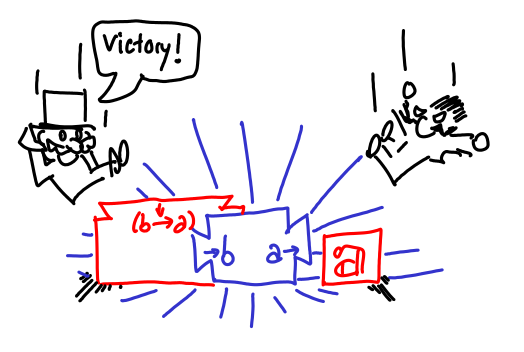
As a proposer, you can take the inputs and machines the verifier gives you, and apply them to each other.
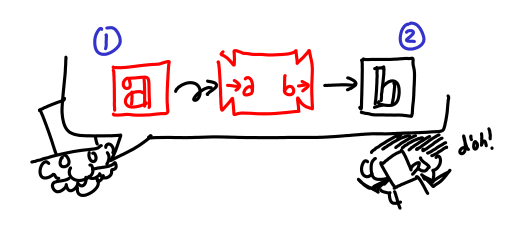
But that's not very interesting. Sometimes, after the verifier gives you some machines, you want to make another proposal. Usually, this is because one of the machines takes a machine which you don’t have, but you also know how to make.
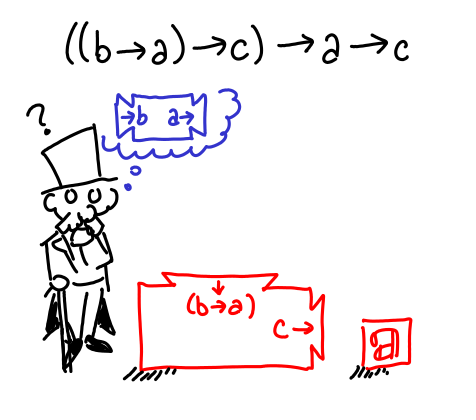
The verifier is obligated to furnish more assumptions for this new proposal, but these are placed inside the cloud of abstraction.
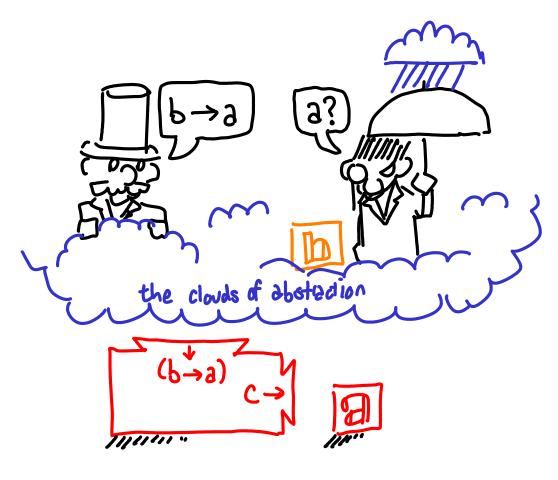
You can use assumptions that the verifier furnished previously (below the cloud of abstraction),

but once you’ve finished the proposal, all of the new assumptions go away. All you’re left with is a shiny new machine (which you ostensibly want to pass to another machine) which can be used for the original goal.
These are all the rules we need for now. (They constitute the most useful subset of what you can do in constructive logic.)
Let’s play a game.
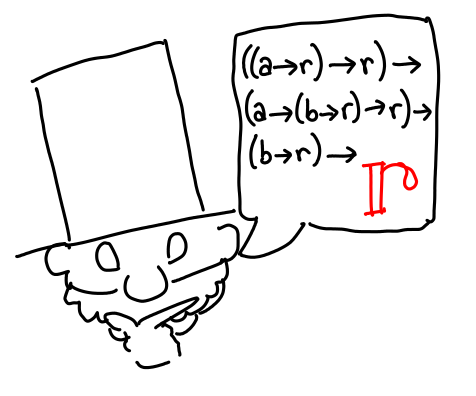
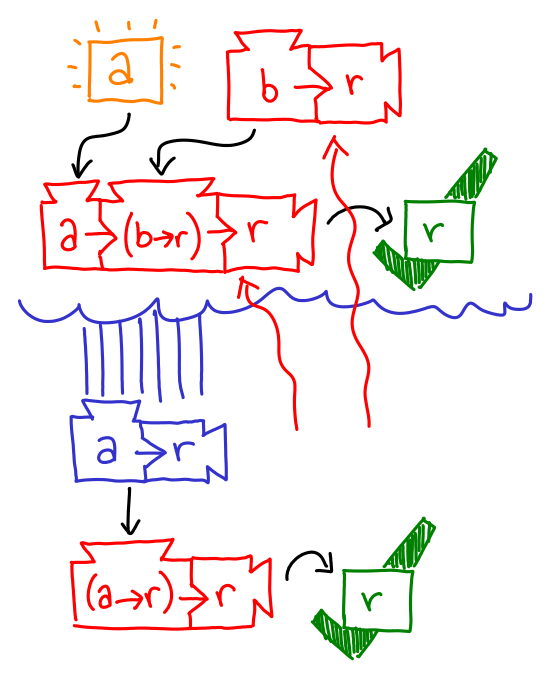
Our verifier supplies the machines we need to play this game. Our goal is r.
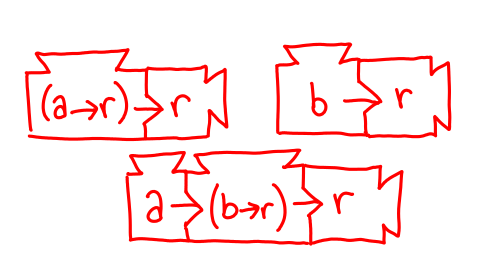
That’s a lot of machines, and it doesn't look like we can run any of them. There's no way we can fabricate up an a from scratch to run the bottom one, so maybe we can make a a -> r. (It may seem like I’ve waved this proposal up for thin air, but if you look carefully it’s the only possible choice that will work in this circumstance.) Let’s make a new proposal for a -> r.
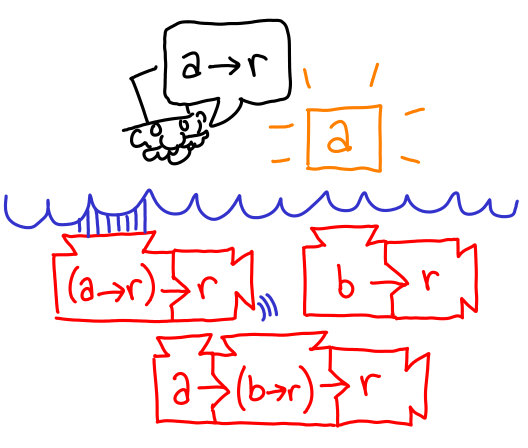
Our new goal for this sub-proposal is also r, but unlike in our original case, we can create an r with our extra ingredient: an a: just take two of the original machines and the newly furnished a. Voila, an r!
This discharges the cloud of abstraction, leaving us with a shiny new a -> r to pass to the remaining machine, and fulfill the original goal with.
Let's give these machines some names. I’ll pick some suggestive ones for you.
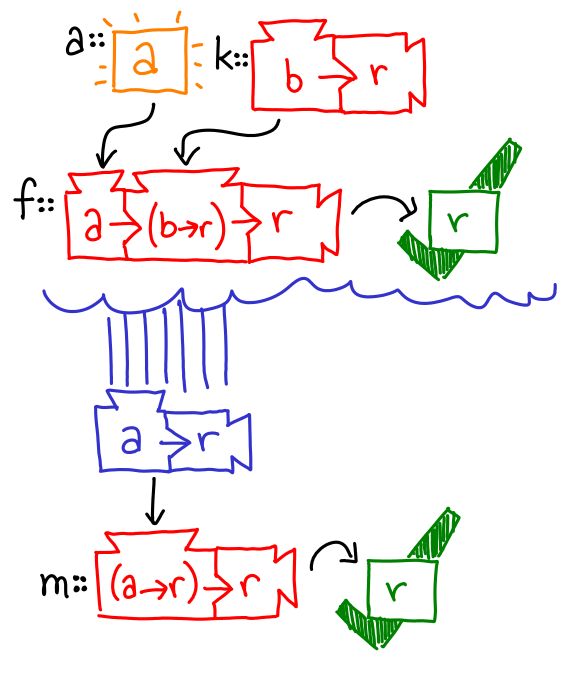
Oh hey, you just implemented bind for the continuation monad.
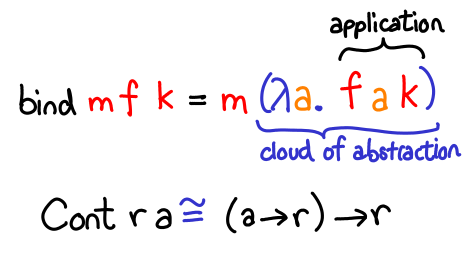
Here is the transformation step by step:
m a -> (a -> m b) -> m b Cont r a -> (a -> Cont r b) -> Cont r b ((a -> r) -> r) -> (a -> ((b -> r) -> r)) -> ((b -> r) -> r) ((a -> r) -> r) -> (a -> (b -> r) -> r) -> (b -> r) -> r
The last step is perhaps the most subtle, but can be done because arrows right associate.
As an exercise, do return :: a -> (a -> r) -> r (wait, that looks kind of familiar...), fmap :: (a -> b) -> ((a -> r) -> r) -> (b -> r) -> r and callCC :: ((a -> (b -> r) -> r) -> (a -> r) -> r) -> (a -> r) -> r (important: that’s a b inside the first argument, not an a !).
This presentation is the game semantic account of intuitionistic logic, though I have elided treatment of negation and quantifiers, which are more advanced topics than the continuation monad, at least in this setting.