An insufficiently lazy map
Another common thunk leak arises from mapping functions over containers, which do not execute their combining function strictly. The usual fix is to instead use a strict version of the function, ala foldl' or insertWith', or perhaps using a completely strict version of the structure. In today’s post, we’ll look at this situation more closely. In particular, the questions I want to answer are as follows:
- Why do we need to create strict and lazy versions of these functions—why can’t these leaks be fixed by the user adding appropriate bang-patterns to some functions?
- Though introducing a stricter API is usually the correct fix, in some circumstances, the problem is not that the API is insufficiently strict, but that the data structure is too insufficiently lazy (that is, inappropriately spine strict.) That is to say, what do I mean by an insufficiently lazy map?
- For data structures in which spine-strictness is necessary, is there any reason that this strictness should not extend to the values themselves? I want to argue that in fact, all spine strict data structures should also be value strict. This may be a bit controversial.
Example
Our example is a very simple data structure, the spine-strict linked list:
data SpineStrictList a = Nil | Cons a !(SpineStrictList a)
ssFromList [] l = l
ssFromList (x:xs) l = ssFromList xs (Cons x l)
ssMap _ Nil l = l
ssMap f (Cons x xs) l = ssMap f xs (Cons (f x) l)
main = do
let l = ssFromList ([1..1000000] :: [Int]) Nil
f x = ssMap permute x Nil
evaluate (f (f (f (f (f (f (f (f l))))))))
permute y = y * 2 + 1
We first create an instance of the data structure using the ssFromList, and then we perform a map over all of its elements using ssMap. We assume the structure of the list is not semantically important (after all, the distribution of trees in an opaque data structure is of no interest to the user, except maybe for performance reasons. In fact, ssFromList and ssMap reverse the structure whenever they’re called, in order to avoid stack overflows.) The space leak here exemplifies the classic “non-strict container function” problem, where a call to a function like map looks harmless but actually blows up.
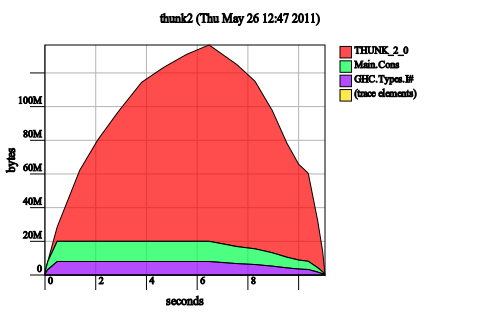
If you look at the implementation, this is not too surprising, based on a cursory look at SpineStrictList: of course it will accumulate thunks since it is not strict in the values, only the structure itself. Let’s look at some of the fixes.
Fixes
Bang-pattern permute. This fix is tempting, especially if you were thinking of our last example:
permute !y = y * 2 + 1
But it’s wrong. Why is it wrong? For one thing, we haven’t actually changed the semantics of this function: it’s already strict in y! The resulting seq is too deeply embedded in the expression; we need permute y to be invoked earlier, not y. Also, remember that fixing our combining function last time only worked because we managed to enable a GHC optimization which unboxed the tuples, avoiding allocating them at all. However, that won’t work here, because we have a strict data structure which GHC doesn’t know if it can get rid of, so all of the allocation will always happen.
Rnf the structure on every iteration. This works, but is pretty inelegant and inefficient. Essentially, you end up traversing every time, for ultimately quadratic runtime, just to make sure that everything is evaluated. rnf is a pretty heavy hammer, and it’s generally a good idea to avoid using it.
Use a strict version of ssMap. This is a pretty ordinary response that anyone who has every changed a function from foo to the foo' version has learned to try:
ssMap' _ Nil l = l ssMap' f (Cons x xs) l = ssMap' f xs ((Cons $! f x) l)
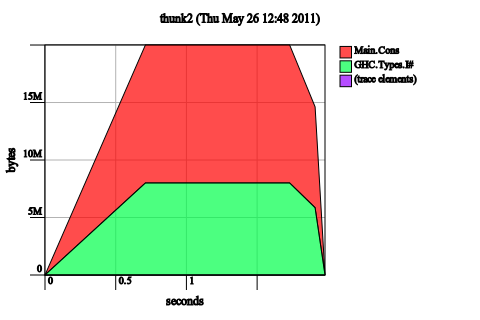
The remaining space usage is merely the strict data structure sitting in memory. In order to make this fix, that we had to go in and fiddle with the internal representation of our SpineStrictList in order to induce this strictness. Here is the answer to question one: we can’t fix this space leak by modifying the combining function, because the extra strictness we require needs to be “attached” (using a seq) to the outer constructor of the data structure itself: something you can only access if you’re able to manipulate the internal structure of the data structure.
One upshot of this is that it’s quite annoying when your favorite container library fails to provide a strict version of a function you need. In fact, historically this has been a problem with the containers package, though I’ve recently submitted a proposal to help fix this.
Make the structure value strict. This is a “nicer” way of turning ssMap into its strict version, since the bang patterns will do all the seq work for you:
data StrictList a = Nil | Cons !a !(SpineStrictList a)
Of course, if you actually want a spine strict but value lazy list, this isn’t the best of worlds. However, in terms of flexibility, a fully strict data structure actually is a bit more flexible. This is because you can always simulate the value lazy version by adding an extra indirection:
data Lazy a = Lazy a type SpineStrictList a = StrictList (Lazy a)
Now the constructor Lazy gets forced, but not necessarily its insides. You can’t pull off this trick with a lazy data structure, since you need cooperation from all of the functions to get the inside of the container evaluated at all. There is one downside to this approach, however, which is that the extra wrapper does have a cost in terms of memory and pointer indirections.
Make the structure lazy. Fascinatingly enough, if we add laziness the space leak goes away:
data SpineStrictList a = Nil | Cons a (SpineStrictList a)
instance NFData a => NFData (SpineStrictList a) where
rnf Nil = ()
rnf (Cons x xs) = rnf x `seq` rnf xs
main = do
let l = ssFromListL ([1..1000000] :: [Int])
f x = ssMapL permute x
evaluate (rnf (f (f (f (f (f (f (f (f l)))))))))
ssFromListL [] = Nil
ssFromListL (x:xs) = Cons x (ssFromListL xs)
ssMapL _ Nil = Nil
ssMapL f (Cons x xs) = Cons (f x) (ssMapL f xs)
We’ve added an rnf to make sure that everything does, in fact, get evaluated. In fact, the space usage dramatically improves!
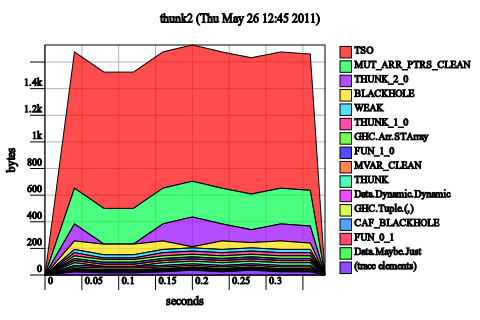
What happened? The trick is that because the data structure was lazy, we didn’t actually bother creating 1000000 thunks at once; instead, we only had thunks representing the head and the tail of the list at any given time. Two is much smaller than a million, and the memory usage is correspondingly smaller. Furthermore, because rnf doesn’t need to hold on to elements of the list after it has evaluated them, we manage to GC them immediately afterwards.
Fusion. If you remove our list-like data constructor wrapper and use the built-in list data type, you will discover that GHC is able to fuse-away all of the maps into one, extremely fast, unboxed operation:
main = do
let l = [1..1000000] :: [Int]
f x = map permute x
evaluate (rnf (f (f (f (f (f (f (f (f l)))))))))
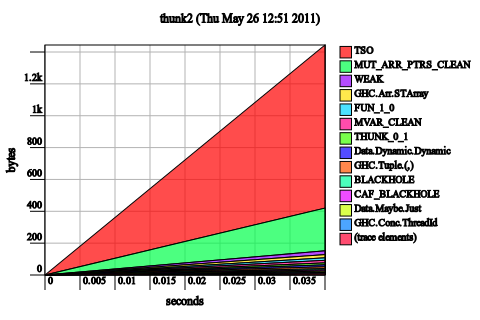
This is not completely fair: we could have managed the same trick with our strict code; however, we cannot use simple foldr/build fusion, which does not work for foldl (recursion with an accumulating parameter.) Nor can we convert our functions to foldr without risking stack overflows on large inputs (though this may be acceptable in tree-like data structures which can impose a logarithmic bound on the size of their spine.) It’s also not clear to me if fusion derives any benefit from spine strictness, though it definitely can do better in the presence of value strictness.
Commentary
In this post, we discussed how to fix the common accumulation of thunks inside spine-strict data structures. What we found was that if the structure was lazy in its structure, the rampant accumulation of thunks is avoided since not all of the leafs have thunks applied to them, and we found that if the structure was strict in its values, the thunks could also be avoided. We also discovered that, for a spine-strict value-lazy structure, the library itself must provide value-strict versions of all of their functions: these functions cannot be easily implemented by the user.
The conclusion I draw from all of these facts is that the spine-strict, value-lazy data structure is a very specialized beast that should only be used in very rare situations. It can be perhaps used to implement a memotable or dynamic programming, but in the event of updates and other “modification” functions, such a structure will almost never do what an ordinary user expects it to do. It should be noted that this does not mean that laziness is the problem: as we saw, many modifications to structures can be streamed, resulting in much better space usage. This is a point we will return to when we discuss streaming leaks. However, it is unclear if we can profitably convert existing spine-strict data structures into spine-lazy ones without paying large indirection costs. That is a topic of ongoing research.