Hoopl guided tour: Base system
Hoopl is a higher-order optimization library. We think it’s pretty cool! This series of blog post is meant to give a tutorial-like introduction to this library, supplementing the papers and the source code. I hope this series will also have something for people who aren’t interested in writing optimization passes with Hoopl, but are interested in the design of higher-order APIs in Haskell. By the end of this tutorial, you will be able to understand references in code to names such as analyzeAndRewriteFwd and DataflowLattice, and make decode such type signatures as:
analyzeAndRewriteFwd :: forall m n f e x entries. (CheckpointMonad m, NonLocal n, LabelsPtr entries) => FwdPass m n f -> MaybeC e entries -> Graph n e x -> Fact e f -> m (Graph n e x, FactBase f, MaybeO x f)
We assume basic familiarity with functional programming and compiler technology, but I will give asides to introduce appropriate basic concepts.
Aside: Introduction. People already familiar with the subject being discussed can feel free to skip sections that are formatted like this.
We will be giving a guided tour of the testing subdirectory of Hoopl, which contains a sample client. (You can grab a copy by cloning the Git repository git clone git://ghc.cs.tufts.edu/hoopl/hoopl.git). You can get your bearings by checking out the README file. The first set of files we’ll be checking out is the “Base System” which defines the data types for the abstract syntax tree and the Hoopl-fied intermediate representation.
The abstract syntax is about as standard as it gets (Ast.hs):
data Proc = Proc { name :: String, args :: [Var], body :: [Block] }
data Block = Block { first :: Lbl, mids :: [Insn], last :: Control }
data Insn = Assign Var Expr
| Store Expr Expr
data Control = Branch Lbl
| Cond Expr Lbl Lbl
| Call [Var] String [Expr] Lbl
| Return [Expr]
type Lbl = String
We have a language of named procedures, which consist of basic blocks. We support unconditional branches Branch, conditional branches Cond, function calls Call (the [Var] is the variables to store the return values, the String is the name of the function, the [Expr] are the arguments, and the Lbl is where to jump to when the function call is done), and function returns Return (multiple return is supported, thus [Expr] rather than Expr).
We don’t have any higher-level flow control constructs (the language's idea of control flow is a lot of gotos—don’t worry, this will work in our favor), so we might expect it to be very easy to map this “high-level assembly language” to machine code fairly easily, and this is indeed the case (very notably, however, this language doesn't require you to think about register allocation, but how we use variables will very noticeably impact register allocation). A real-world example of high-level assembly languages includes C--.
Here is a simple example of some code that might be written in this language:
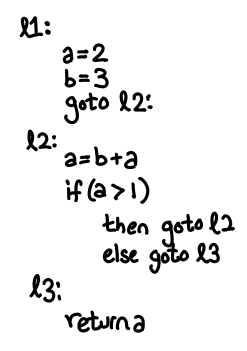
Aside: Basic blocks. Completely explaining what an abstract syntax tree (AST) is a bit beyond the scope of this post, but you if you know how to write a Scheme interpreter in Haskell you already know most of the idea for the expressions component of the language: things like binary operators and variables (e.g. a + b). We then extend this calculator with low-level imperative features in the obvious way. If you’ve done any imperative programming, most of these features are also familiar (branches, function calls, variable assignments): the single new concept is that of the basic block. A basic block is an atomic unit of flow control: if I’ve entered a basic block, I know that I will emerge out the other end, no ifs, ands or buts. This means that there will be no nonlocal transfer of control from inside the block (e.g. no exceptions), and there will be no code that can jump to a point inside this block (e.g. no goto). Any control flow occurs at the end of the basic block, where we may unconditionally jump to another block, or make a function call, etc. Real programs won't be written this way, but we easily convert them into this form, and we will want this style of representation because it will make it easier to do dataflow analysis. As such, our example abstract syntax tree doesn’t really resemble an imperative language you would program in, but it is easily something you might target during code generation, so the example abstract-syntax tree is setup in this manner.
Hoopl is abstract over the underlying representation, but unfortunately, we can’t use this AST as it stands; Hoopl has its own graph representation. We wouldn’t want to use our representation anyway: we’ve represented the control flow graph as a list of blocks [Block]. If I wanted to pull out the block for some particular label; I’d have to iterate over the entire list. Rather than invent our own more efficient representation for blocks (something like a map of labels to blocks), Hoopl gives us a representation Graph n e x (it is, after all, going to have to operate on this representation). The n stands for “node”, you supply the data structure that makes up the nodes of the graph, while Hoopl manages the graph itself. The e and the x parameters will be used to store information about what the shape of the node is, and don’t represent any particular data.
Here is our intermediate representation (IR.hs):
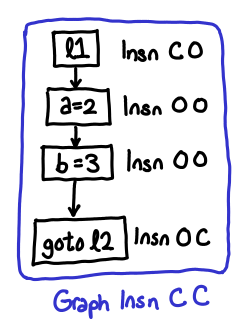
data Proc = Proc { name :: String, args :: [Var], entry :: Label, body :: Graph Insn C C }
data Insn e x where
Label :: Label -> Insn C O
Assign :: Var -> Expr -> Insn O O
Store :: Expr -> Expr -> Insn O O
Branch :: Label -> Insn O C
Cond :: Expr -> Label -> Label -> Insn O C
Call :: [Var] -> String -> [Expr] -> Label -> Insn O C
Return :: [Expr] -> Insn O C
The notable differences are:
- Proc has Graph Insn C C as its body, rather than [Block]. Also, because Graph has no conception of a “first” block, we have to explicitly say what the entry is with entry.
- Instead of using String as Lbl, we’ve switched to a Hoopl provided Label data type.
- Insn, Control and Label have all been squashed into a single Insn generalized abstract data type (GADT) that handles all of them.
Importantly, however, we’ve maintained the information about what shape the node is via the e and x parameters. e stands for entry, x stands for exit, O stands for open, and C stands for closed. Every instruction has a shape, which you can imagine to be a series of pipes, which you are connecting together. Pipes with the shape C O (closed at the entrance, open at the exit) start the block, pipes with the shape O C (open at the entrance, closed at the exit) end the block, and you can have any number of O O pipes in-between. We can see that Insn C O corresponds to our old data type Ast.Lbl, Insn O O corresponds to Ast.Insn, and Insn O C corresponds to Ast.Control. When we put nodes together, we get graphs, which also can be variously open or closed.
Aside: Generalized Abstract Data Types. GADTs are an indispensable swiss army knife for type-level programming. In this aside, we briefly describe some tricks (ala subtyping) that can be used with Insn e x we gave above.
The first “trick” is that you can ignore the phantom type variable entirely, and use Insn like an ordinary data type:
isLabel :: Insn e x -> Bool isLabel Label{} = True isLabel _ = FalseI can pass this function a Label and it will return me True, or I can pass it a Branch and it will return me False. Pattern-matching on the GADT does not result in type refinement that I care about in this particular example, because there is no type variable e or x in the fields of any of the constructors or the return type of the function.
Of course, I could have written this function in such a way that it would be impossible to pass something that is not a Label to it:
assertLabel :: Insn C O -> Bool assertLabel Label{} = TrueIf you try making a call assertLabel (Branch undefined), you’ll get this nice type error from GHC:
<interactive>:1:13: Couldn't match expected type `C' against inferred type `O' Expected type: Insn C O Inferred type: Insn O C In the first argument of `assertLabel', namely `(Branch undefined)' In the expression: assertLabel (Branch undefined)Let’s unpack this: any constructor Branch will result in a value of type Insn O C. However, the type signature of our function states Insn C O, and C ≠ O. The type error is quite straight-forward, and exactly enough to tell us what’s gone wrong!
Similarly, I can write a different function:
transferMiddle :: Insn O O -> Bool transferMiddle Assign{} = True transferMiddle Store{} = FalseThere’s no type-level way to distinguish between Assign and Store, but I don’t have to provide pattern matches against anything else in the data type: Insn O O means I only need to handle constructors that fit this shape.
I can even partially specify what the allowed shapes are:
transferMiddleOrEnd :: Insn O x -> BoolFor this function, I would need to provide pattern matches against the instructions and the control operators, but not a pattern match for IR.Label. This is not something I could have done easily with the original AST: I would have needed to create a sum type Ast.InsnOrControl.
Quick question. If I have a function that takes Insn e x as an argument, and I’d like to pass this value to a function that only takes Insn C x, what do I have to do? What about the other way around?
Exercise. Suppose you were designing a Graph representation for Hoopl, but you couldn’t use GADTs. What would the difference between a representation Graph IR.Insn (where IR.Insn is just like our IR GADT, but without the phantom types) and a representation Graph Ast.Label Ast.Insn Ast.Control?
The last file we’ll look at today is a bit of plumbing, for converting abstract syntax trees into the intermediate representation, Ast2ir.hs. Since there’s some name overloading going on, we use A. to prefix data types from Ast and I. to prefix data types from IR. The main function is astToIR:
astToIR :: A.Proc -> I.M I.Proc
astToIR (A.Proc {A.name = n, A.args = as, A.body = b}) = run $
do entry <- getEntry b
body <- toBody b
return $ I.Proc { I.name = n, I.args = as, I.body = body, I.entry = entry }
The code is monadic because as we convert Strings into Labels (which are internally arbitrary, unique integers), we need to keep track of what labels we’ve already assigned so that same string turns into the same label. The monad itself is an ordinary state monad transformer on top of a “fresh labels” monad. (There’s actually another monad in the stack; see IR.M for more details, but it’s not used at this stage so we ignore it.)
getEntry looks at the first block in the body of the procedure and uses that to determine the entry point:
getEntry :: [A.Block] -> LabelMapM Label getEntry [] = error "Parsed procedures should not be empty" getEntry (b : _) = labelFor $ A.first b
labelFor is a monadic function that gets us a fresh label if we’ve never seen the string Lbl name before, or the existing one if we already have seen it.
toBody uses some more interesting Hoopl functions:
toBody :: [A.Block] -> LabelMapM (Graph I.Insn C C)
toBody bs =
do g <- foldl (liftM2 (|*><*|)) (return emptyClosedGraph) (map toBlock bs)
getBody g
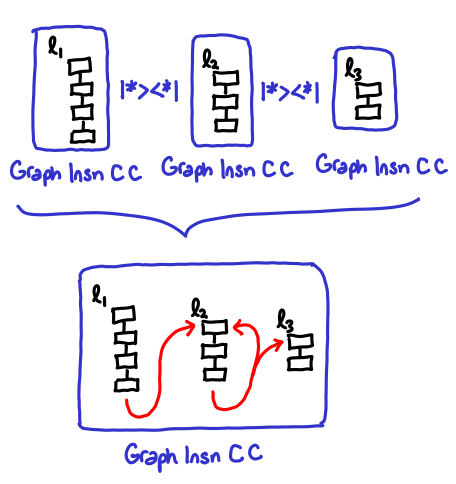
The Hoopl provided functions here are |*><*| and emptyClosedGraph. Note that Hoopl graphs don’t have to be connected (that is, they can contain multiple basic blocks), thus |*><*| is a kind of graph concatenation operator that connects two closed graphs together (Graph n e C -> Graph n C x -> Graph n e x), that might be connected via an indirect control operator (we have no way of knowing this except at runtime, though—thus those arrows are drawn in red). It’s a bit of an unwieldy operator, because Hoopl wants to encourage you to use <*> as far as possible.
toBlock gives an example of <*>:
toBlock :: A.Block -> LabelMapM (Graph I.Insn C C)
toBlock (A.Block { A.first = f, A.mids = ms, A.last = l }) =
do f' <- toFirst f
ms' <- mapM toMid ms
l' <- toLast l
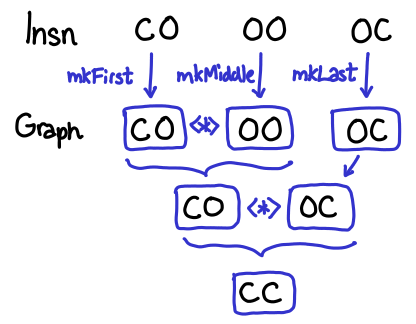
return $ mkFirst f' <*> mkMiddles ms' <*> mkLast l'
We work our way from the bottom up. What are the types of mkFirst f', mkMiddle ms', and mkLast l'? They’re all (Graph I.Insn e x), but f' is C O, ms' is O O, and l' is O C. We build up partial graphs, which are not closed on both sides, and then join them together using <*>, which requires join point between both graphs to be open: Graph n e O -> Graph n O x -> Graph n e x. mkFirst and mkMiddles and mkLast are functions provided by Hoopl that lift I.Insn e x into (Graph I.Insn e x) (or, in the case of mkMiddles, [I.Insn O O]).
And finally, toFirst, toMid and toLast actually perform the translation:
toFirst :: A.Lbl -> LabelMapM (I.Insn C O)
toFirst = liftM I.Label . labelFor
toMid :: A.Insn -> LabelMapM (I.Insn O O)
toMid (A.Assign v e) = return $ I.Assign v e
toMid (A.Store a e) = return $ I.Store a e
toLast :: A.Control -> LabelMapM (I.Insn O C)
toLast (A.Branch l) = labelFor l >>= return . I.Branch
toLast (A.Cond e t f) = labelFor t >>= \t' ->
labelFor f >>= \f' -> return (I.Cond e t' f')
toLast (A.Call rs f as l) = labelFor l >>= return . I.Call rs f as
toLast (A.Return es) = return $ I.Return es
Notice that we’re careful to specify the return shapes, so that we can use mkFirst, mkMiddles and mkLast. The most interesting thing that happens is we have to convert Lbl strings into Label; otherwise, the code is trivial.
That wraps it up for data representation, next time we’ll look at analysis of dataflow facts in Hoopl.