ezyang’s blog

Between packing and hacking on GHC, I didn’t have enough time to cough up the next post of the series or edit the pictures for the previous post, so all you get today is a small errata post.

• The full list diagram is missing some orderings: ★:⊥ ≤ ★:⊥:⊥ and so on.
• In usual denotational semantics, you can’t distinguish between ⊥ and λ_.⊥. However, as Anders Kaseorg and the Haskell Report point out, with seq you can distinguish them. This is perhaps the true reason why seq is a kind of nasty function. I’ve been assuming the stronger guarantee (which is what zygoloid pointed out) when it’s not actually true for Haskell.
• The “ought to exist” arrow in the halts diagram goes the wrong direction.
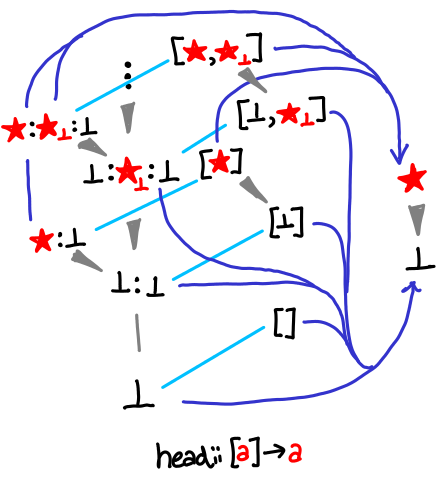
• In the same fashion of the full list diagram, head is missing some orderings, so in fact they gray blob is entirely connected. There are situations when we can have disconnected blobs, but not for a domain with only one maximum.
• Obvious typo for fst.
• The formal partial order on functions was not defined correctly: it originally stated that for f ≤ g, f(x) = g(x); actually, it’s weaker than that: f(x) ≤ g(x).
• A non-erratum: the right-side of the head diagram is omitted because... adding all the arrows makes it look pretty ugly. Here is the sketch I did before I decided it wasn’t a good picture.

Thanks Anders Kaseorg, zygoloid, polux, and whoever pointed out the mistake in the partial order on functions (can’t find that correspondence now) for corrections.

Non sequitur. Here is a really simple polyvariadic function. The same basic idea is how Text.Printf works. May it help you in your multivariadic travels.

{-# LANGUAGE FlexibleInstances #-}

class PolyDisj t where
    disj :: Bool -> t

instance PolyDisj Bool where
    disj x = x
instance PolyDisj t => PolyDisj (Bool -> t) where
    disj x y = disj (x || y)