You could have invented zippers
In the beginning, there was a binary tree:
struct ctree { // c for children
int val;
struct ctree *left;
struct ctree *right;
}
The flow of pointers ran naturally from the root of the tree to the leaves, and it was easy as blueberry pie to walk to the children of a node.
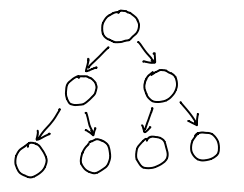
Unfortunately, given a node, there was no good way to find out its parent! If you only needed efficient parent access, though, you could just use a single pointer in the other direction:
struct ptree { // p for parent
int val;
struct ptree *parent;
}
The flow of pointers then ran from the leaves of the tree to the root:
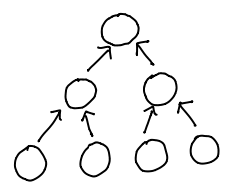
And of course, put together, you could have the best of both worlds:
struct btree {
int val;
struct btree *parent;
struct btree *left;
struct btree *right;
}
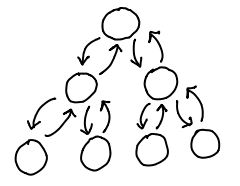
Our data structure had become circular, but as a result we had extremely efficient ways to walk up and down the tree, as well as insert, delete and move nodes, simply by mutating the relevant pointers on our node, its children and its parent.
Trouble in paradise. Pointer tricks are fine and good for the mutable story, but we want immutable nodes. We want nodes that won't change under our nose because someone else decided to muck around the pointer.
In the case of ctree, we can use a standard practice called path copying, where we only need to change the nodes in the path to the node that changed.
In fact, path copying is just a specific manifestation of the rule of immutable updates: if you replace (i.e. update) something, you have to replace anything that points to it, recursively. In a ptree, we'd need to know the subtree of the updated node and change all of them.
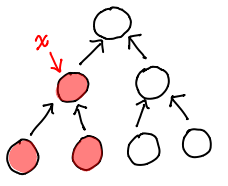
But btree fails pretty spectacularly:
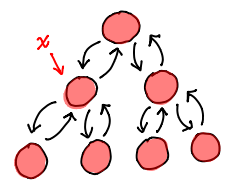
Our web of pointers has meant we need to replace every single node in the tree! The extra circular pointers work to our detriment when looking for a persistent update.
What we'd like to do is somehow combine the ptree and the ctree more intelligently, so we don't end up with a boat of extra pointers, but we still can find the children and the parent of a node.
Here, we make the critical simplifying assumption: we only care about efficient access of parents and children as well as updates of a single node. This is not actually a big deal in a world of immutable data structures: the only reason to have efficient updates on distinct nodes is to have a modification made by one code segment show up in another, and the point of immutability is to stop that spooky action at a distance.
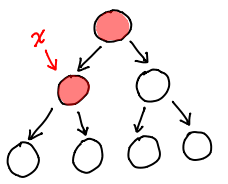
So, on a single node, we want fast access to the parent and children and fast updates. Fast access means we need pointers going away from this node, fast updates means we need to eliminate pointers going into this node.
Easy! Just flip some pointers (shown in red.)
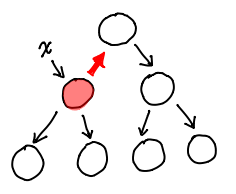
Congratulations, the data structure you see here is what we call a zipper! The only task left for us now is to figure out how we might actually encode this in a struct definition. In the process, we'll assign some names to the various features inside this diagram.
Let's consider a slightly more complicated example:
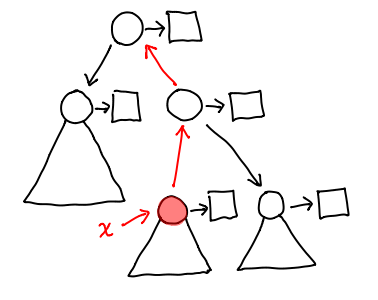
We've introduced a few more notational conveniences: triangles represent the tree attached to a given node when we don't care about any of its subnodes. The squares are the values attached to any given node (we've shown them explicitly because the distinction between the node and its data is important.) The red node is the node we want to focus around, and we've already gone and flipped the necessary pointers (in red) to make everything else accessible.
When we're at this location, we can either traverse the tree, or go up the red arrow pointed away from the green node; we'll call the structure pointed to by this arrow a context. The combination of a tree and a context gives us a location in the zipper.
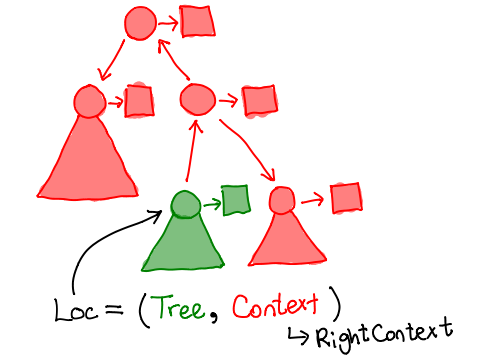
struct loc {
struct ctree *tree;
struct context *context;
}
The context, much like the tree, is a recursive data-structure. In the diagram below, it is precisely the node shaded in black. It's not a normal node, though, since it's missing one of its child pointers, and may contain a pointer to its own parent.
The particular one that this location contains is a "right context", that is, the arrow leading to the context points to the right (shown in black in the following diagram).
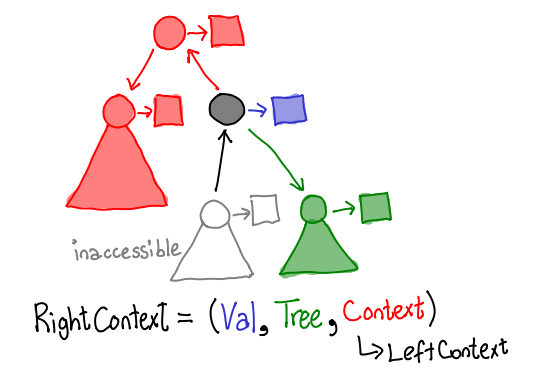
As you can see, for our tree structure, a context contains another context, a tree, and a value.
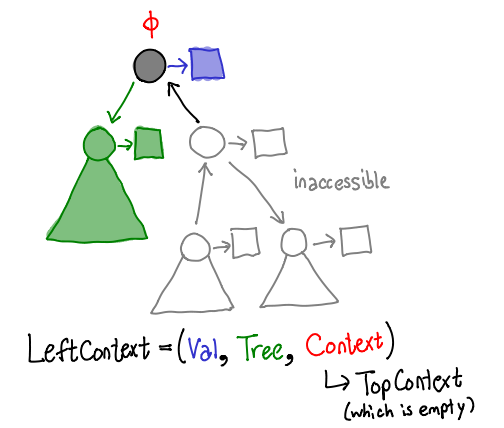
Similarly, a "left context" corresponds to an arrow pointing to the left. It contains the same components, although it may not be quite obvious from the diagram here: where's the recursive subcontext? Well, since we're at the top of the tree, instead we have a "top context", which doesn't contain any values. It's the moral equivalent of Nothing.
enum context_type {LEFT, RIGHT, TOP}
struct context {
enum context_type type;
// below only filled for LEFT and RIGHT
int val;
struct context *context;
struct ctree *tree;
}
And there we have it! All the pieces you need to make a zipper:
> data Tree a = Nil | Node a (Tree a) (Tree a) > data Loc a = Loc (Tree a) (Context a) > data Context a = Top > | Left a (Tree a) (Context a) > | Right a (Tree a) (Context a)
Exercises:
- Write functions to move up, down-left and down-right our definition of Tree.
- If we had the alternative tree definition data Tree a = Leaf a | Branch Tree a) (Tree a), how would our context definition change?
- Write the data and context types for a linked list.
Further reading: The original crystallization of this pattern can be found in Huet's paper (PDF), and two canonical sources of introductory material are at Wikibooks and Haskell Wiki. From there, there is a fascinating discussion about how the differentiation of a type results in a zipper! See Conor's paper (PDF), the Wikibooks article, and also Edward Kmett's post on using generating functions to introduce more exotic datatypes to the discussion.