ezyang’s blog

Optimizing incremental compilation

When you run make to build software, you expect a build on software that has been previously built to take less time than software we are building from scratch. The reason for this is incremental compilation: by caching the intermediate results of ahead-of-time compilation, the only parts of a program that must be recompiled are those that depend on the changed portions of the dependency graph.

The term incremental compilation doesn't say much about how the dependency graph is set up, which can lead to some confusion about the performance characteristics of "incremental compilers." For example, the Wikipedia article on incremental compilation claims that incremental compilers cannot easily optimize the code that it compiles. This is wrong: it depends entirely on how your dependency graph is set up.

Take, for example, gcc for C:

The object file a.o depends on a.c, as well as any header files it (transitively) includes (a.h, in this case.) Since a.o and main.o do not depend on each other, if a.c is rebuilt, main.o does not need to rebuilt. In this sense, C is actually amazingly incremental (said no C programmer ever.) The reason C has a bad reputation for incremental compilation is that, naively, the preprocessing of headers is not done incrementally at all (precompiled headers are an attempt to address this problem).

The dependency graph implies something else as well: unless the body of a function is placed in a.h, there is no way for the compiler that produces main.o to inline the body in: it knows nothing about the C file. a.c may not even exist at the point main.o is being built (parallelism!) The only time such optimization could happen is at link-time (this is why link-time optimization is a thing.)

A nice contrast is ghc for Haskell:

Here, Main.{hi,o} depend not only on Main.hs but A.hi, the module it imports. GHC is still incremental: if you modify an hs file, only things that import that source file that need to be recompiled. Things are even better than this dependency diagram implies: Main.{hi,o} may only depend on specific pieces of A.hi; if those pieces are unchanged GHC will exit early and report compilation is NOT necessary.

Despite being incremental, GHC supports inlining, since unfoldings of functions can be stored in hi files, which can subsequently be used by modules which import it. But now there is a trade-off: if you inline a function, you now depend on the unfolding in the hi file, making it more likely that compilation is necessary when A.hi changes.

As one final example, incremental compilers in IDEs, like the Java compiler in Eclipse, are not doing anything fundamentally different than the operation of GHC. The primary differences are (1) the intermediate products are held in memory, which can result in huge savings since parsing and loading interfaces into memory is a huge timewaster, and (2) they try to make the dependency diagram as fine-grained as possible.

This is all fairly well known, so I want to shift gears and think about a less well-understood problem: how does one do incremental compilation for parametrized build products? When I say parametrized, I mean a blend of the C and Haskell paradigms:

Separate compilation. It should be possible to depend on an interface without depending on an implementation (like when a C file depends on a header file.)
Cost-free abstraction. When the implementation is provided, we should (re)compile our module so that we can inline definitions from the implementation (like when a Haskell module imports another module.)

This problem is of interest for Backpack, which introduces libraries parametrized over signatures to Haskell. For Backpack, we came up with the following design: generate distinct build products for (1) uninstantiated code, for which we know an interface but not its implementation, and (2) instantiated code, for which we know all of their implementations:

In the blue box, we generate A.hi and Main.hi which contain purely the results of typechecking against an interface. Only in the pink box do we combine the implementation of A (in the red box) with the user of A (Main). This is just a graph; thus, incremental compilation works just as it works before.

We quickly ran into an intriguing problem when we sought to support multiple interfaces, which could be instantiated separately: if a client instantiates one interface but not the other, what should we do? Are we obligated to generate build products for these partially instantiated modules? This is not very useful, since we can't generate code yet (since we don't know all of the implementations.)

An important observation is that these interfaces are really cheap to generate (since you're not doing any compilation). Thus, our idea was to do the instantiation on-the-fly, without actually generating build products. The partially instantiated interfaces can be cached in memory, but they're cheap to generate, and we win if we don't need them (in which case we don't instantiate them.)

This is a bit of a clever scheme, and cleverness always has a dark side. A major source of complexity with on-the-fly instantiation is that there are now two representations of what is morally the same build product: the on-the-fly products and the actually compiled ones:

The subtyping relation between these two products states that we can always use a compiled interface in place of an on-the-fly instantiated one, but not vice versa: the on-the-fly interface is missing unfoldings and other important information that compiled code may need.

If we are type-checking only (we have uninstantiated interfaces), we might prefer on-the-fly interfaces, because they require less work to create:

In contrast, if we are compiling a package, we must use the compiled interface, to ensure we see the necessary unfoldings for inlining:

A particularly complicated case is if we are type-checking an uninstantiated set of modules, which themselves depend on some compiled interfaces. If we are using an interface p+a/M.hi, we should be consistent about it, and since r must use the compiled interfaces, so must q:

The alternative is to ensure that we always build products available that were typechecked against the on-the-fly interfaces, as below:

But this has the distasteful effect of requiring everything to be built twice (first typechecked against the on-the-fly interfaces, and then built for real).

The dependency graphs of build products for an ahead-of-time compiler is traditionally part of the public API of a compiler. As I've written previously, to achieve better incrementality, better parallelism, and more features (like parametrized modules), dependency graphs become more and more complicated. When compiler writers don't want to commit to an interface and build tool authors aren't interested learning about a complicated compilation model, the only systems that work well are the integrated ones.

Is Backpack's system for on-the-fly interface instantiation too clever for its own good? I believe it is well-designed for the problem it tries to solve, but if you still have a complicated design, perhaps you are solving the wrong problem. I would love to hear your thoughts.

What Template Haskell gets wrong and Racket gets right

Why are macros in Haskell terrible, but macros in Racket great? There are certainly many small problems with GHC's Template Haskell support, but I would say that there is one fundamental design point which Racket got right and Haskell got wrong: Template Haskell does not sufficiently distinguish between compile-time and run-time phases. Confusion between these two phases leads to strange claims like “Template Haskell doesn’t work for cross-compilation” and stranger features like -fexternal-interpreter (whereby the cross-compilation problem is “solved” by shipping the macro code to the target platform to be executed).

The difference in design can be seen simply by comparing the macro systems of Haskell and Racket. This post assumes knowledge of either Template Haskell, or Racket, but not necessarily both.

Basic macros. To establish a basis of comparison, let’s compare how macros work in Template Haskell as opposed to Racket. In Template Haskell, the primitive mechanism for invoking a macro is a splice:

{-# LANGUAGE TemplateHaskell #-}
module A where
val = $( litE (intPrimL 2) )

Here, $( ... ) indicates the splice, which runs ... to compute an AST which is then spliced into the program being compiled. The syntax tree is constructed using library functions litE (literal expression) and intPrimL (integer primitive literal).

In Racket, the macros are introduced using transformer bindings, and invoked when the expander encounters a use of this binding:

#lang racket
(define-syntax macro (lambda (stx) (datum->syntax #'int 2)))
(define val macro)

Here, define-syntax defines a macro named macro, which takes in the syntax stx of its usage, and unconditionally returns a syntax object representing the literal two (constructed using datum->syntax, which converts Scheme data into ASTs which construct them).

Template Haskell macros are obviously less expressive than Racket's (an identifier cannot directly invoke a macro: splices are always syntactically obvious); conversely, it is easy to introduce a splice special form to Racket (hat tip to Sam Tobin-Hochstadt for this code—if you are not a Racketeer don’t worry too much about the specifics):

#lang racket
(define-syntax (splice stx)
    (syntax-case stx ()
        [(splice e) #'(let-syntax ([id (lambda _ e)]) (id))]))
(define val (splice (datum->syntax #'int 2)))

I will reuse splice in some further examples; it will be copy-pasted to keep the code self-contained but not necessary to reread.

Phases of macro helper functions. When writing large macros, it's frequently desirable to factor out some of the code in the macro to a helper function. We will now refactor our example to use an external function to compute the number two.

In Template Haskell, you are not allowed to define a function in a module and then immediately use it in a splice:

{-# LANGUAGE TemplateHaskell #-}
module A where
import Language.Haskell.TH
f x = x + 1
val = $( litE (intPrimL (f 1)) ) -- ERROR
-- A.hs:5:26:
--     GHC stage restriction:
--       ‘f’ is used in a top-level splice or annotation,
--       and must be imported, not defined locally
--     In the splice: $(litE (intPrimL (f 1)))
-- Failed, modules loaded: none.

However, if we place the definition of f in a module (say B), we can import and then use it in a splice:

{-# LANGUAGE TemplateHaskell #-}
module A where
import Language.Haskell.TH
import B (f)
val = $( litE (intPrimL (f 1)) ) -- OK

In Racket, it is possible to define a function in the same file you are going to use it in a macro. However, you must use the special-form define-for-syntax which puts the function into the correct phase for a macro to use it:

#lang racket
(define-syntax (splice stx)
    (syntax-case stx ()
        [(splice e) #'(let-syntax ([id (lambda _ e)]) (id))]))
(define-for-syntax (f x) (+ x 1))
(define val (splice (datum->syntax #'int (f 1))))

If we attempt to simply (define (f x) (+ x 1)), we get an error “f: unbound identifier in module”. The reason for this is Racket’s phase distinction. If we (define f ...), f is a run-time expression, and run-time expressions cannot be used at compile-time, which is when the macro executes. By using define-for-syntax, we place the expression at compile-time, so it can be used. (But similarly, f can now no longer be used at run-time. The only communication from compile-time to run-time is via the expansion of a macro into a syntax object.)

If we place f in an external module, we can also load it. However, we must once again indicate that we want to bring f into scope as a compile-time object:

(require (for-syntax f-module))

As opposed to the usual (require f-module).

Reify and struct type transform bindings. In Template Haskell, the reify function gives Template Haskell code access to information about defined data types:

{-# LANGUAGE TemplateHaskell #-}
module A where
import Language.Haskell.TH
data Single a = Single a
$(reify ''Single >>= runIO . print >> return [] )

This example code prints out information about Single at compile time. Compiling this module gives us the following information about List:

TyConI (DataD [] A.Single [PlainTV a_1627401583]
   [NormalC A.Single [(NotStrict,VarT a_1627401583)]] [])

reify is implemented by interleaving splices and typechecking: all top-level declarations prior to a top-level splice are fully typechecked prior to running the top-level splice.

In Racket, information about structures defined using the struct form can be passed to compile-time via a structure type transformer binding:

#lang racket
(require (for-syntax racket/struct-info))
(struct single (a))
(define-syntax (run-at-compile-time stx)
  (syntax-case stx () [
    (run-at-compile-time e)
      #'(let-syntax ([id (lambda _ (begin e #'(void)))]) (id))]))
(run-at-compile-time
  (print (extract-struct-info (syntax-local-value (syntax single)))))

Which outputs:

'(.#<syntax:3:8 struct:single> .#<syntax:3:8 single>
   .#<syntax:3:8 single?> (.#<syntax:3:8 single-a>) (#f) #t)

The code is a bit of a mouthful, but what is happening is that the struct macro defines single as a syntax transformer. A syntax transformer is always associated with a compile-time lambda, which extract-struct-info can interrogate to get information about the struct (although we have to faff about with syntax-local-value to get our hands on this lambda—single is unbound at compile-time!)

Discussion. Racket’s compile-time and run-time phases are an extremely important idea. They have a number of consequences:

You don’t need to run your run-time code at compile-time, nor vice versa. Thus, cross-compilation is supported trivially because only your run-time code is ever cross-compiled.
Your module imports are separated into run-time and compile-time imports. This means your compiler only needs to load the compile-time imports into memory to run them; as opposed to Template Haskell which loads all imports, run-time and compile-time, into GHC's address space in case they are invoked inside a splice.
Information cannot flow from run-time to compile-time: thus any compile-time declarations (define-for-syntax) can easily be compiled prior to performing expanding simply by ignoring everything else in a file.

Racket was right, Haskell was wrong. Let’s stop blurring the distinction between compile-time and run-time, and get a macro system that works.

Postscript. Thanks to a tweet from Mike Sperber which got me thinking about the problem, and a fascinating breakfast discussion with Sam Tobin-Hochstadt. Also thanks to Alexis King for helping me debug my extract-struct-info code.

Further reading. To learn more about Racket's macro phases, one can consult the documentation Compile and Run-Time Phases and General Phase Levels. The phase system is also described in the paper Composable and Compileable Macros.

Debugging tcIfaceGlobal errors in GHC: a study in interpreting trace output

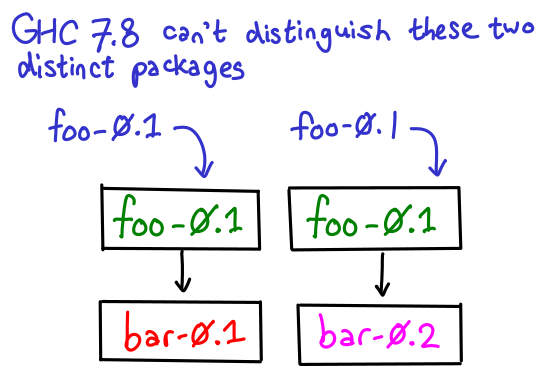
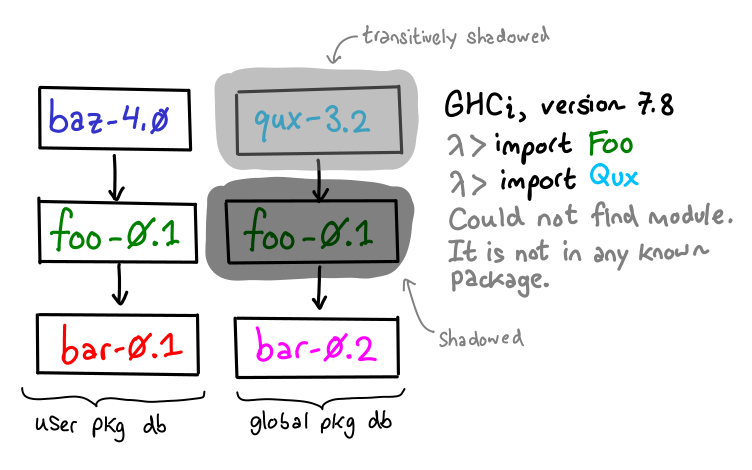
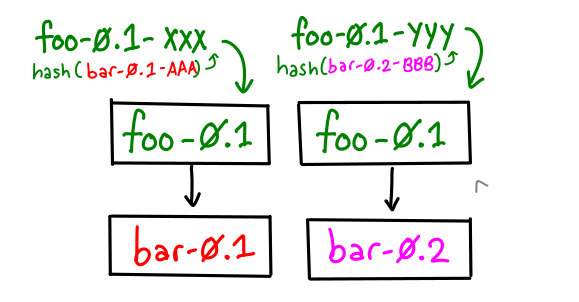
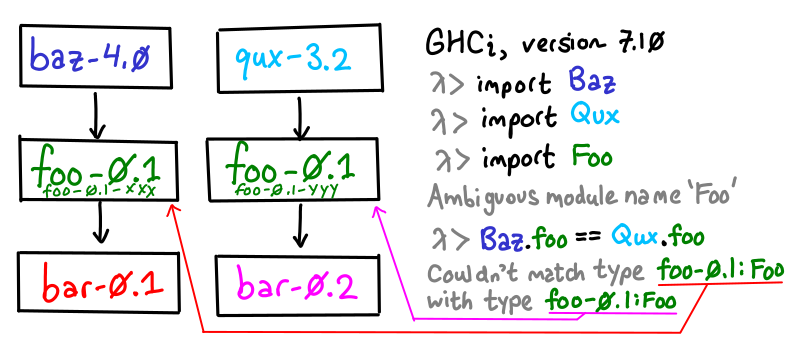
I recently solved a bug where GHC was being insufficiently lazy (yes, more laziness needed!) I thought this might serve as a good blog post for how I solve these sorts of laziness bugs, and might engender a useful conversation about how we can make debugging these sorts of problems easier for people.

Hark! A bug!

Our story begins with an inflight patch for some related changes I’d been working on. The contents of the patch are not really important—it just fixed a bug where ghc --make did not have the same behavior as ghc -c in programs with hs-boot files.

Validating the patch on GHC’s test suite, I discovered that made the prog006 test for GHCi start failing with the following error:

ghc-stage2: panic! (the 'impossible' happened)
  (GHC version 8.1.20160512 for x86_64-unknown-linux):
        tcIfaceGlobal (global): not found
  You are in a maze of twisty little passages, all alike.
  While forcing the thunk for TyThing Data
  which was lazily initialized by initIfaceTcRn,
  I tried to tie the knot, but I couldn't find Data
  in the current type environment.
  If you are developing GHC, please read Note [Tying the knot]
  and Note [Type-checking inside the knot].
  Consider rebuilding GHC with profiling for a better stack trace.
  Contents of current type environment: []

tcIfaceGlobal errors are a “dark” corner of how GHC implements hs-boot files, but since I’d been looking at this part of the compiler for the past week, I decided to boldly charge forward.

If your test case doesn't fit on a slide, it's not small enough

prog006 is not a simple test case, as it involves running the following commands in a GHCi session:

:! cp Boot1.hs Boot.hs
:l Boot.hs
:! sleep 1
:! cp Boot2.hs Boot.hs
:r

While the source files involved are relatively short, my first inclination was to still simplify the test case. My first thought was that the bug involved some aspect of how GHCi reloaded modules, so my first idea was to try to minimize the source code involved:

-- Boot.hs-boot
module Boot where
data Data

-- A.hs
module A where
import {-# SOURCE #-} Boot
class Class a where
  method :: a -> Data -> a

-- Boot1.hs
module Boot where
data Data

-- Boot2.hs
{-# LANGUAGE ExistentialQuantification #-}
module Boot where
import A
data Data = forall n. Class n => D n

This example uses a fancy language feature ExistentialQuantification, and its generally a good bet to try to eliminate these sorts of uses if they are not relevant to the problem at hand. So my first idea was to replace the type class in module A with something more pedestrian, e.g., a type synonym. (Note: why not try to eliminate the hs-boot? In this case, I happened to know that a tcIfaceGlobal error can only occur when compiling an hs-boot file.)

I did this transformation, resulting in the following smaller program:

-- Boot.hs-boot
module Boot
data Data

-- A.hs
module A
import {-# SOURCE #-} Boot
type S = Data

-- Boot.hs
module Boot
import A
x :: S

This program indeed also gave a tcIfaceGlobal error... but then I realized that Boot.hs is not well-typed anyway: it’s missing a declaration for Data! And indeed, when I inserted the missing declaration, the panic went away.

One of the important things in debugging is to know when you have accidentally triggered a different bug. And indeed, this was a different bug, which I reported here.

In the process of reducing this test case I discovered that the bug had nothing to do with GHCi at all; e.g., if I just ran ghc --make Boot2.hs that was sufficient to trigger the bug. (Or, for a version of GHC without my patch in question, running ghc -c Boot2.hs after building the rest—ghc --make has different behavior prior to the patch which started this all masks the bug in question.) So here's the final test-case (with some shorter names to avoid some confusing messages):

-- Boot.hs-boot
module Boot where
data D

-- A.hs
module A where
import {-# SOURCE #-} Boot
class K a where
  method :: a -> D -> a

-- Boot.hs
{-# LANGUAGE ExistentialQuantification #-}
module Boot where
import A
data Data = forall n. K n => D n

Debugging is easier when you know what the problem is

When debugging a problem like this, it helps to have some hypothesis about why the bug is occurring. And to have a hypothesis, we must first ask ourselves the question: what is tcIfaceGlobal doing, anyway?

Whenever you have a panic like this, you should grep for the error message and look at the surrounding source code. Here it is for tcIfaceGlobal (on a slightly older version of GHC which also manifests the bug):

; case if_rec_types env of {    -- Note [Tying the knot]
    Just (mod, get_type_env)
        | nameIsLocalOrFrom mod name
        -> do           -- It's defined in the module being compiled
        { type_env <- setLclEnv () get_type_env         -- yuk
        ; case lookupNameEnv type_env name of
                Just thing -> return thing
                Nothing   -> pprPanic "tcIfaceGlobal (local): not found:"
                                        (ppr name $$ ppr type_env) }

  ; _ -> do

And if you see a Note associated with the code, you should definitely go find it and read it:

-- Note [Tying the knot]
-- ~~~~~~~~~~~~~~~~~~~~~
-- The if_rec_types field is used in two situations:
--
-- a) Compiling M.hs, which indirectly imports Foo.hi, which mentions M.T
--    Then we look up M.T in M's type environment, which is splatted into if_rec_types
--    after we've built M's type envt.
--
-- b) In ghc --make, during the upsweep, we encounter M.hs, whose interface M.hi
--    is up to date.  So we call typecheckIface on M.hi.  This splats M.T into
--    if_rec_types so that the (lazily typechecked) decls see all the other decls
--
-- In case (b) it's important to do the if_rec_types check *before* looking in the HPT
-- Because if M.hs also has M.hs-boot, M.T will *already be* in the HPT, but in its
-- emasculated form (e.g. lacking data constructors).

So case (a) is exactly what's going on here: when we are typechecking Boot.hs and load the interface A.hi, when we typecheck the reference to D, we don’t go and typecheck Boot.hi-boot; instead, we try to tie the knot with the locally defined Data in the module. If Data is not in the type environment, we get the panic we were seeing.

What makes things tricky is that there is no explicit call to "typecheck the reference to D"; instead, this lump of work is unsafely wrapped into a thunk for the TyThing representing D, which is embedded within the description of K. When we force this thunk, GHC will then scurry off and attempt to typecheck the types associated with D.

Back to our original question: why is D not defined in the local type environment? In general, this is because we forced the thunk for K (and thus caused it to call tcIfaceGlobal D) before we actually added D to the type environment. But why did this occur? There seem to be two possible explanations for this:

The first explanation is that we forgot to update the type environment before we forced the thunk. The fix then would be to add some extra updates to the global type environment so that we can see the missing types when we do force the thunk.
The second explanation is that we are forcing the thunk too early, and there is some code that needs to be made lazier so that we only force thunk at the point when the type environment has been updated sufficiently.

So, which is it?

Reading the tea-leaf traces

In both cases, it seems useful to know where in the typechecking process we actually force the thunk. Now here’s the point where I should rebuild GHC with profiling and then get a stack trace out of tcIfaceGlobal, but I was feeling a bit lazy and so I decided to use GHC’s tracing facilities instead.

GHC has existing flags -ddump-tc-trace, -ddump-rn-trace and -ddump-if-trace which dump out a lot of debugging trace information associated with typechecking, renaming and interface loading, respectively. Most of these messages are very terse and don’t say very much about how the message is supposed to be interpreted; if you want to interpret these messages you are going to have to search the source code and see what code is outputting the trace.

Here's the end of the trace we get from compiling, in one-shot mode, Boot.hs:

Tc2 (src)
Tc3
txExtendKindEnv []
txExtendKindEnv []
tcTyAndCl start kind checking ()
kcTyClGroup
  module Boot
    data D = forall n_anU. K n_anU => D
<<some log elided here>>
tc_lhs_type:
  K n_anU
  Constraint
tc_infer_lhs_type: K
lk1 K
Starting fork { Declaration for K
Loading decl for K
updating EPS_
Considering whether to load GHC.Prim {- SYSTEM -}
Reading interface for GHC.Prim;
    reason: Need home interface for wired-in thing TYPE
updating EPS_
tc-iface-class1 K
tc-iface-class2 K
tc-iface-class3 K
tc-iface-class4 K
buildClass
newGlobalBinder A C:K <no location info>
                C:K
newGlobalBinder A $tcK <no location info>
                $tcK
Starting fork { Class op method D -> a
ghc-stage2: panic! (the 'impossible' happened)
<<rest of the panic message>>

Amazingly, this trace actually tells you exactly what you need to know to solve the bug... but we're getting ahead of ourselves. First, we need to know how to interpret this trace.

Each trace message, e.g., Tc2 (src), Tc3, etc., comes with a unique string which you can use to find where the trace originates from. For example, grepping for Tc2 lands you in TcRnDriver.hs, right where we are about to start renaming and typechecking all of the declarations in the source file. Similarly, lk1 lands you in TcHsType.hs, where we are trying to lookup the TyThing associated with K.

The Starting fork messages are of particular interest: this is -ddump-if-trace's way of saying, “I am evaluating a thunk which has some deferred work typechecking interfaces.“ So we can see that shortly after the trace lk1, we force the thunk for the type class declaration K; furthermore, while we are forcing this thunk, we further force the thunk for the class operation method :: D -> a, which actually causes the panic.

The Rube Goldberg machine

I didn’t read the trace closely enough, so I spent some time manually adding extra tracing declarations and tracing the flow of the code during typechecking. Starting with Tc2 (src), we can actually use the trace to follow the flow of typechecking (use of hasktags here is essential!):

tcRnModuleTcRnM is the main entry point for renaming and typechecking a module. After processing imports, it calls tcRnSrcDecls to typecheck the main body.
tcRnSrcDecls calls tc_rn_src_decls to typecheck all of the top-level declarations; then it simplifies all of the top-level constraints and finalizes all the types.
tc_rn_src_decls is the main loop of the Template Haskell / typecheck/renaming dance. We first rename (via rnTopSrcDecls) and typecheck (tcTopSrcDecls) up until the first splice, then run the splice and recurse.
tcTopSrcDecls outputs Tc2 (src). It successively typechecks all the different types of top-level declarations. The big important one is tcTyClsInstDecls which typechecks type and class declarations and handles deriving clauses.
tcTyClsInstDecls calls tcTyAndClassDecls to typecheck top-level type and class declarations, and then calls tcInstDeclsDeriv to handle deriving.
tcTyAndClassDecls takes every mutually recursive group of type/class declarations and calls tcTyClGroup on them.
tcTyClGroup calls tcTyClDecls to typecheck the group and then checks if everything is well-formed.
tcTyClDecls actually type checks the group of declarations. It first kind-checks the group with kcTyClGroup; then it type-checks all of the groups together, tying the knot.
kcTyClGroup outputs the (appropriately named) kcTyClGroup trace. At this point I stopped tracing.

By observing the kcTyClGroup trace, but no terminating kcTyClGroup result trace (which is at the end of this function), we can tell that while we were kind checking, the bad thunk was triggered.

It is actually quite useful to know that the panic occurs while we are kind-checking: kind-checking occurs before we actually construct the knot-tied TyThing structures for these top-level declarations. So we know that it is not the case that we are failing to update the global type environment, because it definitely is not constructed at this point. It must be that we are forcing a thunk too early.

AAAAAAAA is the sound of a GHC disappearing down a black hole

At this point, I was pretty sure that lk1, a.k.a. tcTyVar was responsible for forcing the thunk that ultimately lead to the panic, but I wasn't sure. Here's the code for the function:

tcTyVar :: TcTyMode -> Name -> TcM (TcType, TcKind)
-- See Note [Type checking recursive type and class declarations]
-- in TcTyClsDecls
tcTyVar mode name         -- Could be a tyvar, a tycon, or a datacon
  = do { traceTc "lk1" (ppr name)
       ; thing <- tcLookup name
       ; case thing of
           ATyVar _ tv -> return (mkTyVarTy tv, tyVarKind tv)

           ATcTyCon tc_tc -> do { check_tc tc_tc
                                ; tc <- get_loopy_tc name tc_tc
                                ; handle_tyfams tc tc_tc }
                             -- mkNakedTyConApp: see Note [Type-checking inside the knot]
                 -- NB: we really should check if we're at the kind level
                 -- and if the tycon is promotable if -XNoTypeInType is set.
                 -- But this is a terribly large amount of work! Not worth it.

           AGlobal (ATyCon tc)
             -> do { check_tc tc
                   ; handle_tyfams tc tc }

tcTyVar on K should result in the AGlobal (ATyCon tc), and inserting a trace on that branch didn’t result in any extra output. But I sealed the deal by adding thing `seq` traceTc "lk2" (ppr name) and observing that no lk2 occurred.

It is also clear that it should be OK for us to force K, which is an external declaration, at this point in the code. So something has gone wrong inside the thunk itself.

Back to the tea leaves

Let's take a look at the end of the trace again:

Starting fork { Declaration for K
Loading decl for K
updating EPS_
Considering whether to load GHC.Prim {- SYSTEM -}
Reading interface for GHC.Prim;
    reason: Need home interface for wired-in thing TYPE
updating EPS_
tc-iface-class1 K
tc-iface-class2 K
tc-iface-class3 K
tc-iface-class4 K
buildClass
newGlobalBinder A C:K <no location info>
                C:K
newGlobalBinder A $tcK <no location info>
                $tcK
Starting fork { Class op method D -> a
ghc-stage2: panic! (the 'impossible' happened)
<<rest of the panic message>>

In human readable terms, the trace tells a story like this:

Someone forced the thunk representing the TyThing for the type class K (Starting fork { Declaration for K)
I'm typechecking the contents of the IfaceDecl for K (tc-iface-class, etc.)
I'm building the actual Class representing this type class (buildClass)
I allocate some global names for the class in question. (newGlobalBinder)
Oops! I force the thunk representing class operation method (which has type D -> a)
Shortly after, a panic occurs.

So, it’s off to read the code for TcIface. Here's the body of the code which typechecks an IfaceDecl for a type class declaration:

= bindIfaceTyConBinders binders $ \ tyvars binders' -> do
  { tc_name <- lookupIfaceTop tc_occ
  ; traceIf (text "tc-iface-class1" <+> ppr tc_occ)
  ; ctxt <- mapM tc_sc rdr_ctxt
  ; traceIf (text "tc-iface-class2" <+> ppr tc_occ)
  ; sigs <- mapM tc_sig rdr_sigs
  ; fds  <- mapM tc_fd rdr_fds
  ; traceIf (text "tc-iface-class3" <+> ppr tc_occ)
  ; mindef <- traverse (lookupIfaceTop . mkVarOccFS) mindef_occ
  ; cls  <- fixM $ \ cls -> do
            { ats  <- mapM (tc_at cls) rdr_ats
            ; traceIf (text "tc-iface-class4" <+> ppr tc_occ)
            ; buildClass tc_name tyvars roles ctxt binders' fds ats sigs mindef tc_isrec }
  ; return (ATyCon (classTyCon cls)) }

The methods of a type class are processed in sigs <- mapM tc_sig rdr_sigs. Looking at this helper function, we see:

tc_sig :: IfaceClassOp -> IfL TcMethInfo
tc_sig (IfaceClassOp occ rdr_ty dm)
  = do { op_name <- lookupIfaceTop occ
       ; ~(op_ty, dm') <- forkM (mk_op_doc op_name rdr_ty) $
                          do { ty <- tcIfaceType rdr_ty
                             ; dm' <- tc_dm dm
                             ; return (ty, dm') }
             -- Must be done lazily for just the same reason as the
             -- type of a data con; to avoid sucking in types that
             -- it mentions unless it's necessary to do so
       ; return (op_name, op_ty, dm') }

Great! There is already some code which mentions that the types of the signatures need to be done lazily. If we force op_ty or dm', we will cause the types here to be loaded. So now all we need to do is find where in buildClass these are being forced. Here is the header of buildClass:

buildClass tycon_name tvs roles sc_theta binders
           fds at_items sig_stuff mindef tc_isrec

So let's look for occurrences of sig_stuff. The first place they are used is:

; op_items <- mapM (mk_op_item rec_clas) sig_stuff
                -- Build the selector id and default method id

Let's look at that helper function:

mk_op_item :: Class -> TcMethInfo -> TcRnIf n m ClassOpItem
mk_op_item rec_clas (op_name, _, dm_spec)
  = do { dm_info <- case dm_spec of
                      Nothing   -> return Nothing
                      Just spec -> do { dm_name <- newImplicitBinder op_name mkDefaultMethodOcc
                                      ; return (Just (dm_name, spec)) }
       ; return (mkDictSelId op_name rec_clas, dm_info) }

There it is! The case on dm_spec will force dm', which will in turn cause the type to be forced, which results in a panic. That can’t be right.

It seems that mk_op_item only cares about the top level of wrapping on dm_spec; spec is used lazily inside dm_info, which doesn't appear to be forced later in mkClass. So the fix would be to make it so that when can peel back the outer Maybe without forcing the contents of dm:

--- a/compiler/iface/TcIface.hs
+++ b/compiler/iface/TcIface.hs
@@ -429,20 +429,23 @@ tc_iface_decl _parent ignore_prags
    tc_sig :: IfaceClassOp -> IfL TcMethInfo
    tc_sig (IfaceClassOp occ rdr_ty dm)
      = do { op_name <- lookupIfaceTop occ
-          ; ~(op_ty, dm') <- forkM (mk_op_doc op_name rdr_ty) $
-                             do { ty <- tcIfaceType rdr_ty
-                                ; dm' <- tc_dm dm
-                                ; return (ty, dm') }
+          ; let doc = mk_op_doc op_name rdr_ty
+          ; op_ty <- forkM (doc <+> text "ty") $ tcIfaceType rdr_ty
                 -- Must be done lazily for just the same reason as the
                 -- type of a data con; to avoid sucking in types that
                 -- it mentions unless it's necessary to do so
+          ; dm'   <- tc_dm doc dm
           ; return (op_name, op_ty, dm') }

-   tc_dm :: Maybe (DefMethSpec IfaceType) -> IfL (Maybe (DefMethSpec Type))
-   tc_dm Nothing               = return Nothing
-   tc_dm (Just VanillaDM)      = return (Just VanillaDM)
-   tc_dm (Just (GenericDM ty)) = do { ty' <- tcIfaceType ty
-                                    ; return (Just (GenericDM ty')) }
+   tc_dm :: SDoc
+         -> Maybe (DefMethSpec IfaceType)
+         -> IfL (Maybe (DefMethSpec Type))
+   tc_dm _   Nothing               = return Nothing
+   tc_dm _   (Just VanillaDM)      = return (Just VanillaDM)
+   tc_dm doc (Just (GenericDM ty))
+        = do { -- Must be done lazily to avoid sucking in types
+             ; ty' <- forkM (doc <+> text "dm") $ tcIfaceType ty
+             ; return (Just (GenericDM ty')) }

We check the fix, and yes! It works!

The parting glass

I won’t claim that my debugging process was the most efficient possible—not mentioned in this blog post is the day I spent reading the commit history to try and convince myself that there wasn’t actually a bug where we forgot to update the global type environment. But there seem to be a few generalizable lessons here:

If you see some trace output, the way to make the trace most useful to you is to determine where in the code the trace comes from, and what the compiler is doing at that point in time. Usually, grepping for the trace message is good enough to figure this out.
The smaller your test cases, the smaller your traces will be, which will make it easier to interpret the traces. When I ran my test case using ghc --make rather than ghc -c, there was a lot more logging output. Sure the ending trace is the same but if there was something important in the earlier trace, it would have been that much harder to dig out.
If you can trust your traces, debugging is easier. If I had trusted the trace output, I could have found the bug a lot more quickly. But I didn't, and instead spent a bunch of time making sure the code was behaving in the way I expected it to. On the plus side, I understand the codepath here a lot better than I used to.

How can GHC make debugging these types of bugs easier? Have your own laziness-related debugging story? I would love to hear what you think.

Announcing cabal new-build: Nix-style local builds

cabal new-build, also known as “Nix-style local builds”, is a new command inspired by Nix that comes with cabal-install 1.24. Nix-style local builds combine the best of non-sandboxed and sandboxed Cabal:

Like sandboxed Cabal today, we build sets of independent local packages deterministically and independent of any global state. new-build will never tell you that it can't build your package because it would result in a “dangerous reinstall.” Given a particular state of the Hackage index, your build is completely reproducible. For example, you no longer need to compile packages with profiling ahead of time; just request profiling and new-build will rebuild all its dependencies with profiling automatically.
Like non-sandboxed Cabal today, builds of external packages are cached globally, so that a package can be built once, and then reused anywhere else it is also used. No need to continually rebuild dependencies whenever you make a new sandbox: dependencies which can be shared, are shared.

Nix-style local builds work with all versions of GHC supported by cabal-install 1.24, which currently is GHC 7.0 and later. Additionally, cabal-install is on a different release cycle than GHC, so we plan to be pushing bugfixes and updates on a faster basis than GHC's yearly release cycle.

Although this feature is in only beta (there are bugs, see “Known Issues”, and the documentation is a bit sparse), I’ve been successfully using Nix-style local builds exclusively to do my Haskell development. It's hard to overstate my enthusiasm for this new feature: it “just works”, and you don't need to assume that there is a distribution of blessed, version-pegged packages to build against (e.g., Stackage). Eventually, new-build will simply replace the existing build command.

Quick start

Nix-style local builds “just work”: there is very little configuration that needs to be done to start working with it.

Download and install cabal-install 1.24:
```
cabal update
cabal install cabal-install
```
Make sure the newly installed cabal is in your path.
To build a single Cabal package, instead of running cabal configure; cabal build, you can use Nix-style builds by prefixing these commands with new-; e.g., cabal new-configure; cabal new-build. cabal new-repl is also supported. (Unfortunately, other commands are not yet supported, e.g. new-clean (#2957) or new-freeze (#2996).)
To build multiple Cabal packages, you need to first create cabal.project file in some root directory. For example, in the Cabal repository, there is a root directory with a folder per package, e.g., the folders Cabal and cabal-install. Then in cabal.project, specify each folder:
```
packages: Cabal/
          cabal-install/
```
Then, in the directory for a package, you can say cabal new-build to build all of the components in that package; alternately, you can specify a list of targets to build, e.g., package-tests cabal asks to build the package-tests test suite and the cabal executable. A component can be built from any directory; you don't have to be cd'ed into the directory containing the package you want to build. Additionally, you can qualify targets by the package they came from, e.g., Cabal:package-tests asks specifically for the package-tests component from Cabal. There is no need to manually configure a sandbox: add a cabal.project file, and it just works!

Unlike sandboxes, there is no need to add-source; just add the package directories to your cabal.project. And unlike traditional cabal install, there is no need to explicitly ask for packages to be installed; new-build will automatically fetch and build dependencies.

There is also a convenient script you can use for hooking up new-build to your Travis builds.

How it works

Nix-style local builds are implemented with these two big ideas:

For external packages (from Hackage), prior to compilation, we take all of the inputs which would influence the compilation of a package (flags, dependency selection, etc.) and hash it into an identifier. Just as in Nix, these hashes uniquely identify the result of a build; if we compute this identifier and we find that we already have this ID built, we can just use the already built version. These packages are stored globally in ~/.cabal/store; you can list all of the Nix packages that are globally available using ghc-pkg list --package-db=$HOME/.cabal/store/ghc-VERSION/package.db.
For local packages, we instead assign an inplace identifier, e.g., foo-0.1-inplace, which is local to a given cabal.project. These packages are stored locally in dist-newstyle/build; you can list all of the per-project packages using ghc-pkg list --package-db=dist-newstyle/packagedb. This treatment applies to any remote packages which depend on local packages (e.g., if you vendored some dependency which your other dependencies depend on.)

Furthermore, Nix local builds use a deterministic dependency solving strategy, by doing dependency solving independently of the locally installed packages. Once we've solved for the versions we want to use and have determined all of the flags that will be used during compilation, we generate identifiers and then check if we can improve packages we would have needed to build into ones that are already in the database.

Commands

`new-configure FLAGS`

Overwrites cabal.project.local based on FLAGS.

`new-build [FLAGS] [COMPONENTS]`

Builds one or more components, automatically building any local and non-local dependencies (where a local dependency is one where we have an inplace source code directory that we may modify during development). Non-local dependencies which do not have a transitive dependency on a local package are installed to ~/.cabal/store, while all other dependencies are installed to dist-newstyle.

The set of local packages is read from cabal.project; if none is present, it assumes a default project consisting of all the Cabal files in the local directory (i.e., packages: *.cabal), and optional packages in every subdirectory (i.e., optional-packages: */*.cabal).

The configuration of the build of local packages is computed by reading flags from the following sources (with later sources taking priority):

~/.cabal/config
cabal.project
cabal.project.local (usually generated by new-configure)
FLAGS from the command line

The configuration of non-local packages is only affect by package-specific flags in these sources; global options are not applied to the build. (For example, if you --disable-optimization, this will only apply to your local inplace packages, and not their remote dependencies.)

new-build does not read configuration from cabal.config.

Phrasebook

Here is a handy phrasebook for how to do existing Cabal commands using Nix local build:

old-style	new-style
`cabal configure`	`cabal new-configure`
`cabal build`	`cabal new-build`
`cabal clean`	`rm -rf dist-newstyle cabal.project.local`
`cabal run EXECUTABLE`	`cabal new-build; ./dist-newstyle/build/PACKAGE-VERSION/build/EXECUTABLE/EXECUTABLE`
`cabal repl`	`cabal new-repl`
`cabal test TEST`	`cabal new-build; ./dist-newstyle/build/PACKAGE-VERSION/build/TEST/TEST`
`cabal benchmark BENCH`	`cabal new-build; ./dist-newstyle/build/PACKAGE-VERSION/build/BENCH/BENCH`
`cabal haddock`	does not exist yet
`cabal freeze`	does not exist yet
`cabal install --only-dependencies`	unnecessary (handled by `new-build`)
`cabal install`	does not exist yet (for libraries `new-build` should be sufficient; for executables, they can be found in `~/.cabal/store/ghc-GHCVER/PACKAGE-VERSION-HASH/bin`)

cabal.project files

cabal.project files actually support a variety of options beyond packages for configuring the details of your build. Here is a simple example file which displays some of the possibilities:

-- For every subdirectory, build all Cabal files
-- (project files support multiple Cabal files in a directory)
packages: */*.cabal
-- Use this compiler
with-compiler: /opt/ghc/8.0.1/bin/ghc
-- Constrain versions of dependencies in the following way
constraints: cryptohash < 0.11.8
-- Do not build benchmarks for any local packages
benchmarks: False
-- Build with profiling
profiling: true
-- Suppose that you are developing Cabal and cabal-install,
-- and your local copy of Cabal is newer than the
-- distributed hackage-security allows in its bounds: you
-- can selective relax hackage-security's version bound.
allow-newer: hackage-security:Cabal

-- Settings can be applied per-package
package cryptohash
  -- For the build of cryptohash, instrument all functions
  -- with a cost center (normally, you want this to be
  -- applied on a per-package basis, as otherwise you would
  -- get too much information.)
  profiling-detail: all-functions
  -- Disable optimization for this package
  optimization: False
  -- Pass these flags to GHC when building
  ghc-options: -fno-state-hack

package bytestring
  -- And bytestring will be built with the integer-simple
  -- flag turned off.
  flags: -integer-simple

When you run cabal new-configure, it writes out a cabal.project.local file which saves any extra configuration options from the command line; if you want to know how a command line arguments get translated into a cabal.project file, just run new-configure and inspect the output.

Known issues

As a tech preview, the code is still a little rough around the edges. Here are some more major issues you might run into:

Although dependency resolution is deterministic, if you update your Hackage index with cabal update, dependency resolution will change too. There is no cabal new-freeze, so you'll have to manually construct the set of desired constraints.
A new feature of new-build is that it avoids rebuilding packages when there have been no changes to them, by tracking the hashes of their contents. However, this dependency tracking is not 100% accurate (specifically, it relies on your Cabal file accurately reporting all file dependencies ala sdist, and it doesn't know about search paths). There's currently no UI for forcing a package to be recompiled; however you can induce a recompilation fairly easily by removing an appropriate cache file: specifically, for the package named p-1.0, delete the file dist-newstyle/build/p-1.0/cache/build.
On Mac OS X, Haskell Platform, you may get the message “Warning: The package list for 'hackage.haskell.org' does not exist. Run 'cabal update' to download it.” That is issue #3392; see the linked ticket for workarounds.

If you encounter other bugs, please let us know on Cabal's issue tracker.

Hindley-Milner with top-level existentials

Content advisory: This is a half-baked research post.

Abstract. Top-level unpacking of existentials are easy to integrate into Hindley-Milner type inference. Haskell should support them. It's possible this idea can work for internal bindings of existentials as well (ala F-ing modules) but I have not worked out how to do it.

Update. And UHC did it first!

Update 2. And rank-2 type inference is decidable (and rank-1 existentials are an even weaker system), although the algorithm for rank-2 inference requires semiunification.

Background

The difference between Hindley-Milner and System F. Although in informal discussion, Hindley-Milner is commonly described as a “type inference algorithm”, it should properly be described as a type system which is more restrictive than System F. Both type systems allow polymorphism via universal quantification of variables, but in System F this polymorphism is explicit and can occur anywhere, whereas in Hindley-Milner the polymorphism is implicit, and can only occur at the “top level” (in a so-called “polytype” or “type scheme.”) This restriction of polymorphism is the key which makes inference (via Algorithm W) for Hindley-Milner decidable (and practical), whereas inference for System F undecidable.

-- Hindley Milner
id :: a -> a
id = λx. x

-- System F
id :: ∀a. a -> a
id = Λa. λ(x : a). x

Existential types in System F. A common generalization of System F is to equip it with existential types:

Types  τ ::= ... | ∃a. τ
Terms  e ::= ... | pack <τ, e>_τ | unpack <a, x> = e in e

In System F, it is technically not necessary to add existentials as a primitive concept, as they can be encoded using universal quantifiers by saying ∃a. τ = ∀r. (∀a. τ → r) → r.

Existential types in Hindley-Milner? This strategy will not work for Hindley-Milner: the encoding requires a higher-rank type, which is precisely what Hindley-Milner rules out for the sake of inference.

In any case, it is a fool's game to try to infer existential types: there's no best type! HM always infers the most general type for an expression: e.g., we will infer f :: a -> a for the function f = \x -> x, and not Int -> Int. But the whole point of data abstraction is to pick a more abstract type, which is not going to be the most general type and, consequently, is not going to be unique. What should be abstract, what should be concrete? Only the user knows.

Existential types in Haskell. Suppose that we are willing to write down explicit types when existentials are packed, can Hindley-Milner do the rest of the work: that is to say, do we have complete and decidable inference for the rest of the types in our program?

Haskell is an existence (cough cough) proof that this can be made to work. In fact, there are two ways to go about doing it. The first is what you will see if you Google for “Haskell existential type”:

{-# LANGUAGE ExistentialQuantification #-}
data Ex f = forall a. Ex (f a)
pack :: f a -> Ex f
pack = Ex
unpack :: Ex f -> (forall a. f a -> r) -> r
unpack m k = case m of Ex x -> f x

Ex f is isomorphic to ∃a. f a, and similar to the System F syntax, they can be packed with the Ex constructor and unpacked by pattern-matching on them.

The second way is to directly use the System F encoding using Haskell's support for rank-n types:

{-# LANGUAGE RankNTypes #-}
type Ex f = forall r. (forall a. f a -> r) -> r
pack :: f a -> Ex f
pack x = \k -> k x
unpack :: Ex f -> (forall a. f a -> r) -> r
unpack m k = m k

The boxy types paper demonstrated that you can do inference, so long as all of your higher rank types are annotated. Although, perhaps it was not as simple as hoped, since impredicative types are a source of constant bugs in GHC's type checker.

The problem

Explicit unpacks suck. As anyone who has tried programming with existentials in Haskell can attest, the use of existentials can still be quite clumsy due to the necessity of unpacking an existential (casing on it) before it can be used. That is to say, the syntax let Ex x = ... in ... is not allowed, and it is an easy way to get GHC to tell you its brain exploded.

Leijen investigated the problem of handling existentials without explicit unpacks.

Loss of principal types without explicit unpacks, and Leijen's solution. Unfortunately, the naive type system does not have principal types. Leijen gives an example where there is no principal type:

wrap :: forall a. a -> [a]
key  :: exists b. Key b
-- What is the type of 'wrap key'?
-- [exists b. Key b]?
-- exists b. [key b]?

Neither type is a subtype of the other. In his paper, Leijen suggests that the existential should be unwrapped as late as possible (since you can go from the first type to the second, but not vice versa), and thus, the first type should be preferred.

The solution

A different approach. What if we always lift the existential to the top level? This is really easy to do if you limit unpacks to the top-level of a program, and it turns out this works really well. (The downside is that dynamic use of existentials is not supported.)

There's an existential in every top-level Haskell algebraic data type. First, I want to convince you that this is not all that strange of an idea. To do this, we look at Haskell's support for algebraic data types. Algebraic data types in Haskell are generative: each data type must be given a top-level declaration and is considered a distinct type from any other data type. Indeed, Haskell users use this generativity in conjunction with the ability to hide constructors to achieve data abstraction in Haskell. Although there is not actually an existential lurking about—generativity is not data abstraction—generativity is an essential part of data abstraction, and HM has no problem with this.

Top-level generativity corresponds to existentials that are unpacked at the top-level of a program (ala F-ing modules). We don't need existentials embedded inside our Haskell expressions to support the generativity of algebraic data types: all we need is the ability to pack an existential type at the top level, and then immediately unpack it into the top-level context. In fact, F-ing modules goes even further: existentials can always be lifted until they reach the top level of the program. Modular programming with applicative functors (the ML kind) can be encoded using top-level existentials which are immediately unpacked as they are defined.

The proposal. So let us suggest the following type system, Hindley-Milner with top-level existentials (where a* denotes zero to many type variables):

Term variables ∈ f, x, y, z
Type variables ∈ a, b, c

Programs
prog ::= let f = e in prog
       | seal (b*, f :: σ) = (τ*, e) in prog
       | {- -}

Type schemes (polytypes)
σ ::= ∀a*. τ

Expressions
e ::= x
    | \x -> e
    | e e

Monotypes
τ ::= a
    | τ -> τ

There is one new top-level binding form, seal. We can give it the following typing rule:

Γ ⊢ e :: τ₀[b* → τ*]
a* = free-vars(τ₀[b* → τ*])
Γ, b*, (f :: ∀a*. τ₀) ⊢ prog
---------------------------------------------
Γ ⊢ seal (b*, f :: ∀a*. τ₀) = (τ*, e) in prog

It also elaborates directly to System F with existentials:

seal (b*, f :: σ) = (τ*, e) in prog
  ===>
unpack <b*, f> = pack <τ*, e>_{∃b*. σ} in prog

A few observations:

In conventional presentations of HM, let-bindings are allowed to be nested inside expressions (and are generalized to polytypes before being added to the context). Can we do something similar with seal? This should be possible, but the bound existential type variables must be propagated up.
This leads to a second problem: naively, the order of quantifiers must be ∃b. ∀a. τ and not ∀a. ∃b. τ, because otherwise we cannot add the existential to the top-level context. However, there is a "skolemization" trick (c.f. Shao and F-ing modules) by which you can just make b a higher-kinded type variable which takes a as an argument, e.g., ∀a. ∃b. b is equivalent to ∃b'. ∀a. b' a. This trick could serve as the way to support inner seal bindings, but the encoding tends to be quite involved (as you must close over the entire environment.)
This rule is not very useful for directly modeling ML modules, as a “module” is usually thought of as a record of polymorphic functions. Maybe you could generalize this rule to bind multiple polymorphic functions?

Conclusion. And that's as far as I've worked it out. I am hoping someone can tell me (1) who came up with this idea already, and (2) why it doesn't work.

ghc-shake: Reimplementing ghc --make

ghc --make is a useful mode in GHC which automatically determines what modules need to be compiled and compiles them for you. Not only is it a convenient way of building Haskell projects, its single-threaded performance is good too, by reusing the work of reading and deserializing external interface files. However, the are a number of downsides to ghc --make:

Projects with large module graphs have a hefty latency before recompilation begins. This is because ghc --make (re)computes the full module graph, parsing each source file's header, before actually doing any work. If you have a preprocessor, it's even worse.
It's a monolithic build system, which makes it hard to integrate with other build systems if you need something more fancy than what GHC knows how to do. (For example, GHC's painstakingly crafted build system knows how to build in parallel across package boundaries, which Cabal has no idea how to do.)
It doesn't give you any insight into the performance of your build, e.g. what modules take a long time to build or what the big "blocker" modules are.

ghc-shake is a reimplementation of ghc --make using the Shake build system. It is a drop-in replacement for ghc. ghc-shake sports the following features:

Greatly reduced latency to recompile. This is because Shake does not recompute the module graph by parsing the header of every file; it reuses cached information and only re-parses source files which have changed.
If a file is rebuilt (and its timestamp updated) but the build output has not changed, we don't bother recompiling anything that depended on it. This is in contrast to ghc --make, which has to run the recompilation check on every downstream module before concluding there is nothing to do. In fact, ghc-shake never runs the recompilation test, because we reimplemented this dependency structure natively in Shake.
Using -ffrontend-opt=--profile, you can get nice profiling information about your build, including how long it took to build each module, and how expensive it is to change one of the modules.
It's as fast as ghc --make on single-threaded builds. Compare this to ghc-make, another build system which uses Shake to build Haskell. ghc-make does not use the GHC API and must use the (slow) ghc -M to get initial dependency information about your project.
It's accurate. It handles many edge-cases (like -dynamic-too) correctly, and because it is written using the GHC API, it can in principle be feature-for-feature compatible with ghc --make. (It's not currently, but only because I haven't implemented them yet.)

There are some downsides:

Shake build systems require a .shake directory to actual store metadata about the build. This is in contrast to ghc --make, which operates entirely off of the timestamps of build products in your directory.
Because it is directly implemented with the GHC API, it only works with a specific version of GHC (the upcoming GHC 8.0 release).
It needs a patched version of the Shake library, because we have custom rule for building modules based off of Shake's (not exported) file representation. I've reported it here.
There are still some missing features and bugs. The ones I've run into are that (1) we forget to relink in some cases, and (2) it doesn't work for building profiled code.

If you want to use ghc-shake today (not for the faint of heart), try git clone https://github.com/ezyang/ghc-shake and follow the instructions in the README. But even if you're not interested in using it, I think the code of ghc-shake has some good lessons for anyone who wants to write a build system involving Haskell code. One of the most important architectural decisions was to make the rules in ghc-shake not be organized around output files (e.g. dist/build/Data/Foo.hi, as in make) but around Haskell modules (e.g. Data.Foo). Semantic build systems work a lot better than forcing everything into a "file abstraction" (although Shake doesn't quite support this mode of use as well as I would like.) There were some other interesting lessons... but that should be the subject for another blog post!

Where is this project headed? There are a few things I'm considering doing in the not-so-immediate future:

To support multiple GHC versions, we should factor out the GHC specific code into a separate executable and communicate over IPC (hat tip Duncan Coutts). This would also allow us to support separate-process parallel GHC builds which still get to reuse read interface files. In any case, ghc-shake could serve as the blueprint for what information GHC needs to make more easily accessible to build systems.
We could consider moving this code back to GHC. Unfortunately, Shake is a bit too big of a dependency to actually have GHC depend on, but it may be possible to design some abstract interface (hello Backpack!) which represents a Shake-style build system, and then have GHC ship with a simple implementation for --make (but let users swap it out for Shake if they like.)
We can extend this code beyond ghc --make to understand how to build entire Cabal projects (or bigger), ala ToolCabal, a reimplementation of Cabal using Shake. This would let us capture patterns like GHC's build system, which can build modules from all the boot packages in parallel (without waiting for the package to completely finish building first.

P.S. ghc-shake is not to be confused with shaking-up-ghc, which is a project to replace GHC's Makefile-based build system with a Shake based build system.

The convergence of compilers, build systems and package managers

Abstract. The traditional abstraction barriers between compiler, build system and package manager are increasingly ill-suited for IDEs, parallel build systems, and modern source code organization. Recent compilers like go and rustc are equipped with a fully-fledged build systems; semantic build systems like Bazel and Gradle also expect to manage the packaging of software. Does this mean we should jettison these abstraction barriers? It seems worthwhile to look for new interfaces which can accommodate these use-cases.

Traditionally, one can understand the tooling of a programming language in three parts:

The compiler takes a single source file and transforms it into an object file. (Examples: ghc -c, go tool 6g, javac and gcc -c.)
The build system takes a collection of source files (and metadata) and transforms them into the final build product. It does this by invoking the compiler multiple times. (Examples: go build, Setup build, make, ant compile.) Often, the build system also knows how to install the build product in question.
The package manager takes a package name, and retrieves and builds the package and its dependencies, and installs them into some store. It does this by invoking the build systems of each package. (Examples: cabal install, cargo install, maven package.)

This separation constitutes an abstraction barrier which allows these components to be separately provided. For example, a single build system can work with multiple different compilers (gcc versus clang); conversely, a compiler may be invoked from a user's custom build system. A library may be packaged for both its native language package manager as well as a Linux distribution's packaging system; conversely, a package manager may be indifferent to how a library actually gets built. In today's software ecosystem, these abstraction barriers are used heavily, with good effect!

However, there are an increasing number of use-cases which cannot be adequately handled using these abstraction barriers:

A build system needs to know what order to build source files in; however, the canonical source for this information is inside the import/include declarations of the source file. This information must either be duplicated inside the build system, or the build system must call the compiler in order to compute the dependency graph to be used. In any case, a compiler cannot just be a dumb source-to-object-file converter: it must know how to emit dependencies of files (e.g., gcc -M). There is no standardized format for this information, except perhaps a Makefile stub.
The dependency problem is further exacerbated when module dependencies can be cyclic. A build system must know how to resolve cycles, either by compiling strongly connected components of modules at a time, or compiling against "interface" files, which permit separate compilation. This was one of the problems which motivated the Rust developers to not expose a one-source-at-a-time compiler.
The best parallelization can be achieved with a fine-grained dependency graph over source files. However, the most desirable place to implement parallelization is the package manager, as an invocation of the package manager will cause the most code to be compiled. Thus, a system like Bazel unifies both the build system and the package manager, so that parallelism can be achieved over the entire build. (Another example is GHC's build system, which parallelizes compilation of all wired-in packages on a per-module basis.)
IDEs want in-depth information from the compiler beyond a -c style interface. But they cannot invoke the compiler directly, because the only way to invoke the compiler with the right flags and the right environment is via the build system / the package manager. Go's built in build-system means that it can more easily provide a tool like go oracle; otherwise, go oracle would need to be able to accommodate external build systems.
Certain language features are actively hostile to build systems; only the compiler has enough smarts to figure out how to manage the build. Good examples include macros (especially macros that can access the filesystem), other forms of compile-time metaprogramming, and compiler plugins.

Thus, the temptation is to roll up these components into a single monolithic tool that does everything. There are many benefits: a single tool is easier to develop, gives a more uniform user experience, and doesn't require the developers to specify a well-defined API between the different components. The downside? You can't swap out pieces of a monolithic system.

I think it is well worth considering how we can preserve this separation of concerns, even in the face of these features. Unfortunately, I don't know what the correct API is, but here is a strawman proposal: every compiler and build system writer should have an alternative mode which lets a user ask the query, "How do I make $output file?" This mode returns (1) the dependencies of that file, and (2) a recipe for how to make it. The idea is to place the dependency-finding logic in the compiler (the canonical place to put it), while letting an external tool actually handle building the dependencies. But there are a lot of details this proposal doesn't cover.

What do you think about the convergence of compiler, build system and package manager? Do you think they should be monolithic? If not, what do you think the right API to support these new use cases should be? I'd love to know what you think.

What is Stateless User Interface?

The essence of stateless user interface is that actions you take with a program should not depend on implicit state. Stateless interfaces are easier to understand, because an invocation of a command with some arguments will always do the same thing, whereas in a stateful interface, the command may do some different than it did yesterday, because that implicit state has changed and is influencing the meaning of your program.

This philosophy is something any Haskeller should intuitively grasp... but Cabal and cabal-install today fail this ideal. Here are some examples of statefulness in Cabal today:

Running cabal install, the built packages are installed into a "package database", which makes them available for use by GHC.
Running cabal install, the choice of what packages and versions to install depends on the state of the local package database (the current solver attempts to reuse already installed software) and the state of the remote package repository (which says what packages and versions are available.)
Running ./Setup configure saves a LocalBuildInfo to dist/setup-config, which influences further Setup commands (build, register, etc.)

Each of these instances of state imposes complexity on users: how many times do you think you have (1) blown away your local package database because it was irreversibly wedged, (2) had your project stop building because the dependency solver started picking too new version of packages, or (3) had Cabal ask you to reconfigure because some feature wasn't enabled?

State has cost, but it is not here for no reason:

The package database exists because we don't want to have to rebuild all of our packages from scratch every time we want to build something (indeed, this is the whole point of a package manager);
The solver depends on the local package database because users are impatient and want to avoid building new versions packages before they can build their software;
The solver depends on the remote package repository because developers and users are impatient and want to get new releases to users as quickly possible;
The configure caches its information because a user doesn't want to wait to reconfigure the package every time they try to build a package they're working on.

In the face of what is seemingly an inherently stateful problem domain, can stateless user interface prevail? Of course it can.

Sometimes the state is merely being used as a cache. If a cache is blown away, everything should still work, just more slowly. The package database (reason 1) and configuration cache (reason 4) both fall under this banner, but the critical mistake today's Cabal makes is that if you delete this information, things do not "just work". There must be sufficient information to rebuild the cache; e.g., the configuration cache should be supplemented with the actual input to the configure step. (Sometimes, separation of concerns means you simply cannot achieve this. What is ghc to do if you ask it to use the not-in-cache lens package?) Furthermore, the behavior of a system should not vary depending on whether or not the cached data is present or not; e.g., the solver (reason 2) should not make different (semantically meaningful) decisions based on what is cached or not.

Otherwise, it must be possible to explicitly manage the state in question: if the state is a remote package repository (reason 3), there must be a way to pin against some state. (There's a tool that does this and it's called Stack.) While sometimes necessary, explicit state complicates interface and makes it harder to describe what the system can do. Preferably, this state should be kept as small and as centralized as possible.

I don't think anything I've said here is particularly subtle. But it is something that you need to specifically think about; otherwise, you will be seduced by the snare of stateful interface. But if you refuse the siren call and put on the hair shirt, your users will thank you much more for it.

Acknowledgments. These thoughts are not my own: I have to give thanks to Johan Tibell, Duncan Coutts, and Simon Marlow, for discussions which communicated this understanding to me. Any mistakes in this article are my own. This is not a call to action: the Cabal developers recognize and are trying to fix this, see this hackathon wiki page for some mutterings on the subject. But I've not seen this philosophy written out explicitly anywhere on the Internet, and so I write it here for you.

Is no-reinstall Cabal coming to GHC 8.0?

You might be wondering: with the beta release of no-reinstall Cabal, is this functionality be coming to GHC 8.0? (Or even a new release of Cabal, since the no-reinstall feature works with GHC 7.10). Unfortunately, there is a split among the Cabal developers over whether or not the actual no-reinstall behavior should go into Cabal by default as is. Duncan Coutts, in particular, has argued that it's a bad idea to enable no-reinstall without other (unimplemented) changes to Cabal. Since the extra needed changes are not fully implemented yet, it's unclear if Duncan will manage them for GHC 8.0.

I've heard a smattering of feedback that no-reinstall Cabal actually is working just fine for people, so I suspect many people would be in favor of just biting the bullet and putting in the "good" (but not "best") solution into Cabal. But I want to foster an informed discussion, so I'd like to explain what the (known) problems with no-reinstall are.

What is no reinstall?

Currently, GHC and Cabal maintain an invariant in the installed package database that for any package name and version (i.e. (source) package ID), there is at most one matching package in the database:

The arrows indicate a "depends on" relationship: so if you have a database that has bar-0.1, bar-0.2 and an instance of foo-0.1 built against bar-0.1, you aren't allowed to install another instance of foo-0.1 built against bar-0.2 (though you are allowed to install foo-0.2 built against bar-0.2).

If cabal-install wants to install a package with the same package ID as a package already in the database, but with different dependencies, it must destructively overwrite the previous entry to maintain this invariant, pictured below:

/img/cabal-status/destructive-reinstall.png

No reinstall relaxes this invariant, so that "reinstalling" a package with different dependencies just works:

The recently beta released no-reinstall Cabal achieves this with two small features. First, in GHC 7.10, we added the flag --enable-multi-instance to ghc-pkg which makes ghc-pkg no longer error if you attempt to add multiple copies of the same package in the database. Second, in Vishal Agrawal's patchset for Cabal, cabal-install is modified to use this flag, so that the dependency solver no longer has to avoid reinstalls.

However, breaking this invariant has consequences. Let's look at some of them.

Problem 1: It doesn't work on old versions of GHC

Summary: In GHC 7.8 and earlier, it's not possible to directly implement no reinstall (because ghc-pkg will reject it.) And even if it were possible, installing a new instance of a package (which has the same source package ID of an existing package) either (1) causes the old package and all of its dependents to become hidden from the default view of GHC, even though they are still usable, or (2) fails to be exposed in the default view of GHC.

Suppose that a package foo-0.1, which defines a type Foo, and has been compiled twice with different versions of its dependencies:

GHC 7.8 could not distinguish between two compilations of the package: symbols from both packages would live in the foo-0.1 namespace, and colliding symbols would simply be considered the same. Disaster! To avoid this situation, GHC has a shadowing algorithm which remove incompatible packages from its visible set. Here is an example:

We have two package databases, the user database and the global database, laid side-to-side (the user database is "on top"). When there is a conflicting package ID in the combined database, GHC prefers the package from the topmost database: thus, in our example the global foo-0.1 is shadowed (any packages which transitively have it as a dependency are also shadowed). When a package is shadowed, it doesn't exist at all to GHC: GHC will not suggest it or make any mention it exists.

No reinstall requires us to allow these duplicate packages the same database! In this case, GHC will apply shadowing; however, it is not well-defined which package should be shadowed. If GHC chooses to shadow the old package, they "vanish" from GHC's default view (it is as if they do not exist at all); if GHC chooses to shadow the new package, a package that a user just cabal-install'd will be mysteriously absent! Troublesome.

Problem 2: Using multiple instances of the same package is confusing

Summary: In GHC 7.10 or later, multiple instances of the same package may be used together in the same GHC/GHCi session, which can result in confusing type inequalities.

In GHC 7.10, we now use "package keys" to test for type identity. A package key is a source package ID augmented with a hash of the package keys of all the dependencies. This means that GHC no longer needs to apply shadowing for soundness, and you can register duplicates of a package using the --enable-mult-instances flag on ghc-pkg.

However, this can still result in confusing behavior. Consider the previous example in GHC 7.10:

Both versions of foo are visible, and so if we try to import Foo, GHC will complain that it doesn't know which Foo we want. This can be fixed by hiding one package or the other. However, suppose that both baz and qux are exposed, and furthermore, they both export a value foo which has type Foo. These types are "distinct", despite the fact that they are: (1) both named Foo, and (2) come from a package named foo-0.1: they are two different instances of foo-0.1. Confusing!

Problem 3: Nix hashing non-sdist'ed packages is difficult

It is easy to "trick" Cabal into hashing a set of source files which is not representative of the true input of the build system: for example, you can omit files in the other-modules field, or you can modify files in between the time Cabal has computed the source hash and the time it builds the files. And if you can't trust the Nix hash, you now have to worry about what happens when you really need to clobber an old entry in the Nix database (which incorrectly has the "same" hash as what you are attempting to install).

This problem doesn't exist for tarballs downloaded from Hackage, because you can simply hash the tarball and that is guaranteed to be the full set of source for building the file.

Duncan's patchset

To deal with these problems, Duncan has been working on a bigger patchset, with the following properties:

To support old versions of GHC, he is maintaining a separate "default view" package database (which is used by bare invocations of GHC and GHCi) from the actual "Nix store" package database. cabal-install is responsible for maintaining a consistent default view, but also installs everything into the Nix store database.
Nix-style hashing is only done on Hackage packages; local source tree are to be built and installed only into a sandbox database, but never the global database. Thus, an actual Nix hash is only ever computed by cabal-install.
He also wants to make it so that cabal-install's install plan doesn't depend on the local state of the Nix database: it should give the same plan no matter what you have installed previously. This is done by dependency resolving without any reference to the Nix database, and then once IPIDs are calculated for each package, checking to see if they are already built. This plan would also make it possible to support cabal install --enable-profiling without having to blow away and rebuild your entire package database.

Vishal's patchset

Vishal was also cognizant of the problems with the default view of the package database, and he worked on some patches to GHC for support for modifying package environments, which would serve a similar role to Duncan's extra package databases. Unfortunately, these patches have been stuck in code review for a bit now, and they wouldn't help users of old versions of GHC. While the code review process for these patches may get unstuck in the near future, I'm hesitant to place any bets on these changes landing.

Conclusion

My view is that, historically, problems one and two have been the big stated reasons why "no reinstall", while being a simple change, hasn't been added to Cabal as the default mode of operation. However, there's been rising sentiment (I think I can safely cite Simon Marlow in this respect) among some that these problems are overstated, and that we should bite the bullet.

If we want to turn on "no reinstall" before Duncan finishes his patchset (whenever that will be—or maybe someone else will finish it), I think there will need to be some concerted effort to show that these problems are a small price to pay for no reinstall Cabal, and that the Haskell community is willing to pay... at least, until a better implementation comes around.

Help us beta test “no-reinstall Cabal”

Over this summer, Vishal Agrawal has been working on a GSoC project to move Cabal to more Nix-like package management system. More simply, he is working to make it so that you'll never get one of these errors from cabal-install again:

Resolving dependencies...
In order, the following would be installed:
directory-1.2.1.0 (reinstall) changes: time-1.4.2 -> 1.5
process-1.2.1.0 (reinstall)
extra-1.0 (new package)
cabal: The following packages are likely to be broken by the reinstalls:
process-1.2.0.0
hoogle-4.2.35
haskell98-2.0.0.3
ghc-7.8.3
Cabal-1.22.0.0
...

However, these patches change a nontrivial number of moving parts in Cabal and cabal-install, so it would be very helpful to have willing guinea pigs to help us iron out some bugs before we merge it into Cabal HEAD. As your prize, you'll get to run "no-reinstall Cabal": Cabal should never tell you it can't install a package because some reinstalls would be necessary.

Here's how you can help:

Make sure you're running GHC 7.10. Earlier versions of GHC have a hard limitation that doesn't allow you to reinstall a package multiple times against different dependencies. (Actually, it would be useful if you test with older versions of GHC 7.8, but only mostly to make sure we haven't introduced any regressions here.)
git clone https://github.com/ezyang/cabal.git (I've added some extra corrective patches on top of Vishal's version in the course of my testing) and git checkout cabal-no-pks.
In the Cabal and cabal-install directories, run cabal install.
Try building things without a sandbox and see what happens! (When I test, I've tried installing multiple version of Yesod at the same time.)

It is NOT necessary to clear your package database before testing. If you completely break your Haskell installation (unlikely, but could happen), you can do the old trick of clearing out your .ghc and .cabal directories (don't forget to save your .cabal/config file) and rebootstrapping with an old cabal-install.

Please report problems here, or to this PR in the Cabal tracker. Or chat with me in person next week at ICFP. :)

« Older Newer »