Secure multiparty Bitcoin anonymization
Abstract. We describe how secure multi-party sorting can serve as the basis for a Bitcoin anonymization protocol which improves over current centralized “mixing” designs.
Bitcoin is a pseudonymous protocol: while Bitcoin addresses are in principle completely anonymous, all traffic into and out of a wallet is publicly visible. With some simple network analysis collections of addresses can be linked together and identified.
The current state of the art for anonymizing Bitcoins is a mixing service, which is trusted third-party wallet which accepts incoming transactions, and in random increments scheduled at random times in the future, transfers a corresponding quantity to a new wallet of your choice. The result is given any Bitcoin that is distributed from this service, there exist a large number of identities from whom the Bitcoin may have originated.
Mixing services of this kind have a number of notable problems. First, the mixing service must be trusted not to keep logs or otherwise monitor the mixing: if they are compromised, the path of any given Bitcoin can be fully traced. The usual advice for this scenario is to use multiple mixing services, so that all of these services must be compromised before anonymity is lost. Second, the mixing service must be trusted not to turn around and refuse to give you back your funds; this makes such mixing services risky for anonymizing large quantities of Bitcoins. Finally, most mixing services charge a processing fee on top of the usual transaction fee one might expect to pay out for arranging for a Bitcoin transfer.
We propose a decentralized, secure multiparty protocol for implementing a mixing protocol. Such a system has been proposed in abstract (also here); in this post, we describe precisely how to implement it, in particular showing that multi-party sorting (a relatively well-studied algorithmic problem) is sufficient to implement this protocol. This protocol does not require a trusted third party (except to assist in discovery of participants interested in performing the mixing protocol), does not require you to reveal your input-output addresses beyond the ultimate transaction, and can be performed atomically using Bitcoin’s transaction language.
Protocol description
First some preliminaries: the multi-party sorting problem is usually formulated as follows: each party i contributes an input element A[i]. After the protocol is carried out, all parties learn the sorted sequence A in secret shared form, but do not learn who contributed any particular element A[i] of the sequence. Referring to the work of Jónsson, Kreitz and Uddin (2011), we assume this protocol as a primitive: the essential idea behind any multi-party sorting is to construct a fixed size sorting circuit for the inputs, and then use the general framework of multi-party computation on the resulting circuit description.
We now describe the mixing problem. Assume that some number of parties are assembled to mix 1 BTC of coins among themselves. (For now, we assume that every participant has the same number of Bitcoins; we will generalize this later.) In particular, each party i has a input wallet A[i] (with balance of at least 1 BTC) and an output wallet B[i], and will only sign a transaction in which 1 BTC is transferred to its output wallet B[i]. Any adversary participating in this transaction should not be able to learn the B[i] corresponding to A[i], except that it is among the set of output wallets taking part in the transaction.
The protocol proceeds as follows:
- Every participant declares the input wallet it will be participating in the protocol with, and produces a signature to show that they own the wallet. These wallets are publically sorted into A.
- With ordering defined as the numeric value of the public key of each participating output wallet, conduct a secure multi-party sort of all of the output wallets. We now have a sorted list of output wallets B, with no member of the transaction having learned who contributed any given output wallet. Each participant should check if their output wallet is contained in this list (to protect against Byzantine failure); if it is not, they should abort the protocol and destroy their output wallet (its identity has been leaked).
- Construct a transaction transferring 1 BTC from A[0] to B[0] (from the sorted lists), A[1] to B[1], and so forth and broadcast it to all participants. Clients sign the transaction with their input wallet.
- Once all signatures have arrived, the transaction is valid and is broadcast for incorporation into the block chain.
Mixing pools only work if all participants are attempting to mix identical amounts of Bitcoins. In order to manage participants who would like to mix larger amounts of Bitcoins, we suggest maintaining discovery channels for power of two sizes of Bitcoins, e.g. ...1/4 BTC, 1/2 BTC, 1 BTC, 2 BTC, 4 BTC...
Analysis
Step (1) does not mention output wallets, and thus cannot leak information about the input-output correspondence. By definition, step (2) does not leak information about who contributed the output wallet. Furthermore, we don’t even require the sorted result to be secret shared: this sorted list will become public information once the transaction is published in the block chain. The case of aborting the transaction when your output wallet is not present in the result (in the case of Byzantine failure) is delicate: aborting does leak information, and thus you must not use the output wallet in any further transactions. In step (3), assuming that an attacker knows that a mixing transaction is taking place, the deterministic mapping of input to output wallets gives all participants no further bits of information. Thus, this protocol clearly fulfills its security requirements.
One odd thing about this protocol is that no random permutation between participants is explicitly constructed. This might seem unusual, since a natural security property one might expect is for an output wallet to receive its 1 BTC from a uniformly randomly chosen input wallet. However, this condition, while sufficient for anonymity, is not necessary. Just as adding a random permutation destroys all information about the original permutation, replacing the original permutation with a new constant permutation also destroys all information about the original permutation. Furthermore, honest participants will have picked their addresses uniformly at random, so the process of sorting automatically constructs a random permutation between these participants (dishonest participants must be excluded, since they can generate addresses from a skewed probability distributions).
What is the amount of anonymity granted by one round of this protocol? Consider the case where I have 1 BTC in an input wallet tied to my identity, and I participate in a mixing round with n honest participants with a fresh output wallet. Since no information about the source of this output wallet was leaked to the participants, an adversary in the transaction would have a 1/n-1 probability of guessing which output wallet was mine: call this the anonymity factor. In the case of a Sybil attack, the amount of anonymity conferred decreases. If the fraction of attackers is less than some fraction of the participants (for many secret sharing protocols, the magic numbers are 1/2 for passive attackers, and 1/3 for active attackers), then the anonymity factor is still 1/n-1, where n is the number of honest participants; but n is smaller than the number of visible participants in the protocol: the size of the transaction is not necessarily correlated with how anonymous it is! If the number of attackers is above this fraction, then the secret sharing scheme may leak information and no anonymity is gained. This allows for a denial of service attack against a mixing protocol; we describe some mitigation strategies against this attack later. (Note, however, that no matter how many attackers there are, you are guaranteed to not lose any Bitcoins, due to the verification step in (2).)
In practice
As with traditional mixing, a number of precautions should be taken in order to avoid accidentally revealing information about the source of Bitcoins via a side-channel. Consider the case where Alice has 2 BTC tied to her real-world identity, and she would like to anonymously pay 3/4 BTC to Bob.
Alice first prepare by creating a pool of empty wallets, which she will use to carry the anonymized Bitcoins. Alice connects to a tracker for 1 BTC mixing over Tor. (1 BTC is the amount she would like to pay to Bob, rounded up.) She waits a time window to expire for the next mixing, and then as the protocol takes place submits her (public) input wallet and her (anonymous) output wallet. If the protocol fails, she throws out her output wallet and submits a new one next time, and blacklists the misbehaving node if she can figure out who it is.
Once Alice has successfully carried out a mixing, she flips a coin (which comes up tails with probability 1/m). If the coin comes up heads, she waits for another mixing. The number of mixing transactions she is expected to perform is m (obeying the geometric distribution, so selected because it makes all output wallets behave identically with regards to remixing or exiting). Once Alice exits mixing, she now has a wallet containing an anonymous Bitcoin (more precisely, this Bitcoin could be attributable with equal probability to any of the other wallets that she participated in mixes with). She transfers 3/4 BTC to Bob, leaving 1/4 BTC in her wallet.
The remaining Bitcoins in the wallet should now be considered tainted (as they now have a direct relationship to Bob, who may have a public wallet). These Bitcoins should be split into mixable amounts and reanonymized, before used for any other purposes. Even after anonymization, these coins must still be used with care: in particular, they must not be transferred back to the original, public Bitcoin account. In such a situation, the graph structure of mixing transactions looks like this:
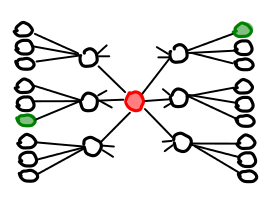
(The green node is your public node, the red node is your anonymous node). Network analysis that looks for cycles in Bitcoin transfers will be able to identify any transactions, even if the anonymizing pool has a large amount of turnover (though, amusingly enough, if many participants generate cycles, this attack is harder to carry out). To assist in the tracking of these coins, we suggest the development of wallet management software that can handle thousands of private keys, sort by “size of coin”, and track the easily traceable transaction history associated with any given coin.
In order to protect herself against Sybil attacks, Alice may wish to select her mixing tracker with care. Some mixing trackers could charge fees for listing: with sufficient volume, these charges would make it more expensive to carry out a sustained Sybil attack. (The fees can then be turned around and used to pay for the processing of the complicated mixing transactions, which have the social expectation of being accompanied with a transaction fee.) Every mixing should be conducted with a different IP address; if Alice is using Tor for anonymity she needs to reanonymize her connection each time.
Conclusion
Secure multi-party computation has always been in the eye of users of Bitcoin seeking anonymization, but to date there has not been any plausible implementation strategy for any such computation. We hope that this document describes such an implementation strategy and leads the way to a better ecosystem of Bitcoin anonymizers. As the fiascos at Bitcoinica and other exchanges have demonstrated, relying on third party wallets is dangerous. Fortunately, they are also unnecessary.
Acknowledgments
I would like to thank Eric Price for playing an instrumental role in the formulation of this protocol.