ezyang's blog

Functions produce the Haskell Heap

We’ve talked about how we open (evaluate) presents (thunks) in the Haskell Heap: we use IO. But where do all of these presents come from? Today we introduce where all these presents come from, the Ghost-o-matic machine (a function in a Haskell program).

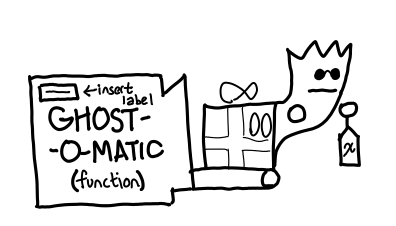
Using a function involves three steps.

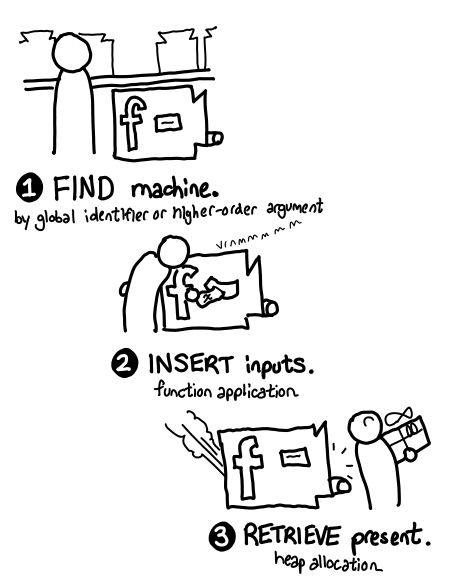
We can treat the machine as a black box that takes present labels and pops out presents, but you can imagine the inside as having an unlimited supply of identical ghosts and empty present boxes: when you run the machine, it puts a copy of the ghost in the box.

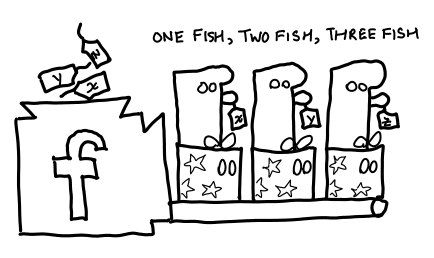
If the ghosts we put into the presents are identical, do they all behave the same way? Yes, but with one caveat: the actions of the ghost are determined by a script (the original source code), but inside the script there are holes that are filled in by the labels you inserted into the machine.

Since there’s not actually anything in the boxes, we can precisely characterize a present by the ghost that haunts it.

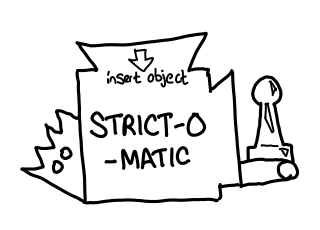
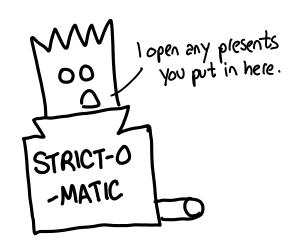
A frequent problem that people who use the Ghost-o-matic run into is that they expect it to work the same way as the Strict-o-matic (a function in a traditional, strictly evaluated language.) They don’t even take the same inputs: the Strict-o-matic takes unwrapped, unhaunted (unlifted) objects and gift cards, and outputs other unhaunted presents and gift cards.

But it’s really easy to forget, because the source-level syntax for strict function application and lazy function application are very similar.

This is a point that must be thoroughly emphasized. In fact, in order to emphasize it, I’ve drawn two more pictures to reiterate what the permitted inputs and outputs for a Ghost-o-matic machine are.

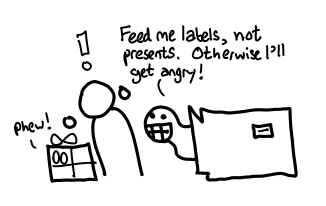
Ghost-o-matics take labels of presents, not the actual presents themselves. This importantly means that the Ghost-o-matic doesn’t open any presents: after all, it only has labels, not the actual present. This stands in contrast to a Strict-o-matic machine which takes presents as inputs and opens them: one might call this machine the force function, of type Thunk a -> a. In Haskell, there is no such thing.

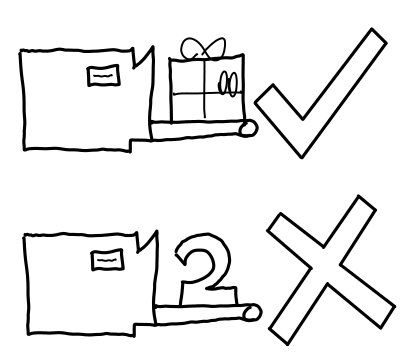
The Ghost-o-matic always creates a wrapped present. It will never produce an unwrapped present, even if there is no ghost haunting the present (the function was a constant).

We state previously that there is no force function in Haskell. But the function seq seems to do something very like forcing a thunk. A present haunted by a seq ghost, when opened, will cause two other presents to be opened (even if the first one is unnecessary). It seems like the first argument is forced; and so seq x x might be some reasonable approximation of force in an imperative language. But what happens when we actually open up a present haunted by the seq ghost?

Although the ghost ends up opening the present rather than us, it’s too late for it to do any good: immediately after the ghost opens the present, we would have gone to open it (which it already is). The key observation is that the seq x x ghost only opens the present x when the present seq x x is opened, and immediately after seq x x is opened we have to go open x by means of an indirection. The strictness of the seq ghost is defeated by the fact that it’s put in a present, not to be opened until x is desired.

One interesting observation is that the Strict-o-matic machine does things when its run. It can open presents, fire missiles or do other side effects.

But the Ghost-o-matic machine doesn’t do any of that. It’s completely pure.

To prevent confusion, users of the Strict-o-matic and Ghost-o-matic machines may find it useful to compare the the present creation life-cycle for each of the machines.

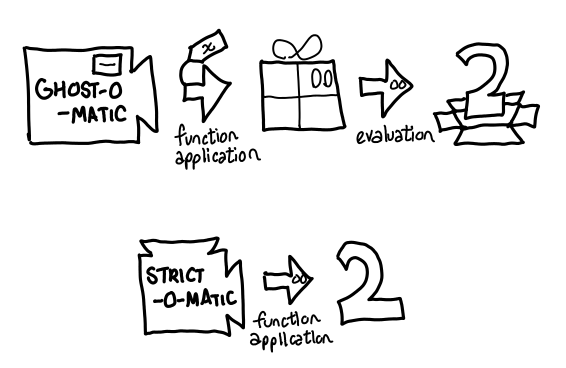
The lazy Ghost-o-matic machine is split into two discrete phases: the function application, which doesn’t actually do anything, just creates the present, and the actual opening of the present. The Strict-o-matic does it all in one bang—although it could output a present (that’s what happens when you implement laziness inside a strict language). But in a strict language, you have to do it all yourself.

The Ghost-o-matic is approved for use by both humans and ghosts.

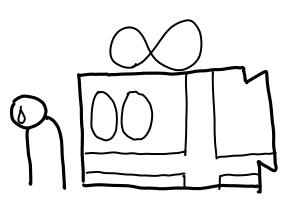
This does mean that opening a haunted present may produces more presents. For example, if the present produces a gift card for presents that don’t already live on the heap.

For a spine-strict data structure, it can produce a lot more presents.

Oh, and one more thing: the Ghost-o-matic makes a great gift for ghosts and family. They can be gift-wrapped in presents too. After all, everything in Haskell is a present.

Technical notes. With optimizations, a function may not necessarily allocate on the heap. The only way to be sure is to check out what optimized Core the program produces. It’s also not actually true that traditional, strict functions don’t exist in Haskell: unboxed primitives can be used to write traditional imperative code. It may look scary, but it’s not much different than writing your program in ML.

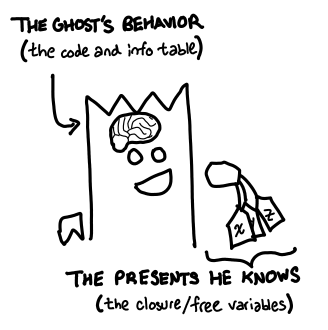
I’ve completely ignored partial application, which ought to be the topic of a later post, but I will note that, internally speaking, GHC does try its very best to pass all of the arguments a function wants at application time; if all the arguments are available, it won’t bother creating a partially application (PAP). But these can be thought of modified Ghost-o-matics, whose ghost already has some (but not all) of its arguments. Gifted ghost-o-matics (functions in the heap) can also be viewed this way: but rather than pre-emptively giving the ghost some arguments, the ghost is instead given its free variables (closure).

Last time: Implementing the Haskell Heap in Python, v1

Next time: How the Grinch stole the Haskell Heap

This work is licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License.