Semi-automatic testing : ezyang’s blog

Semi-automatic testing

When programmers automate something, we often want to go whole-hog and automate everything. But it’s good to remember there’s still a place for manual testing with machine assistance: instead of expending exponential effort to automate everything, automate the easy bits and hard-code answers to the hard research problems. When I was compiling the following graph of sources of test data, I noticed a striking polarization at the ends of "automated" and "non-automated."

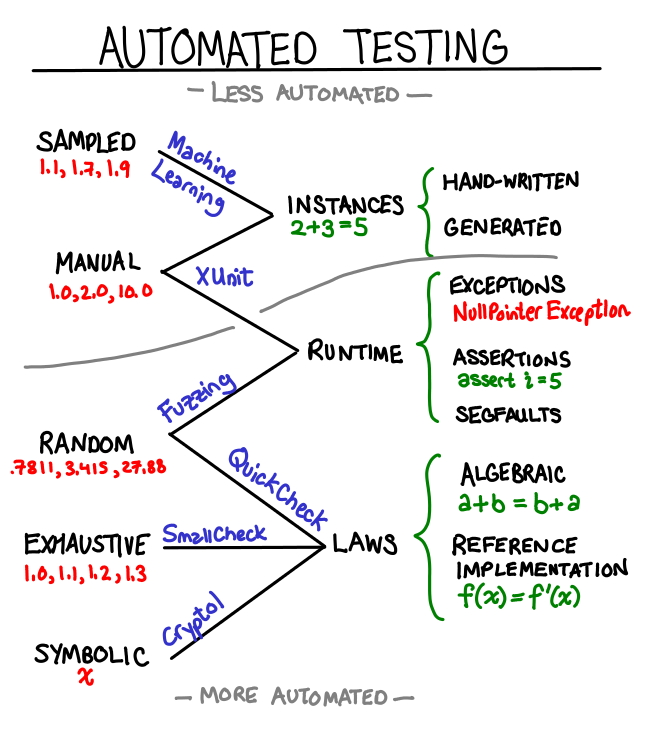
An ideal test framework would support combining all of these data sources and all of these testing mechanisms. Some novel approaches include:

Randomly generated test-cases with manual verification. Obviously you won’t be able to hand verify thousands of test-cases, but a few concrete examples can do wonders for documentation purposes, and random generation prevents us from only picking “nice” inputs.
Reference implementation as previous version of the code. To the limit, you automatically accept the output of an old implementation and save it to your test suite, and when a test starts failing you the framework asks you to check the output, and if it’s “better” than before you overwrite the old test data with the new. GHC’s test suite has something along these lines.
You’ve written lots of algebraic laws, which you are using Quickcheck to verify. You should be able to swap out the random generator with a deterministic stream of data from a sampled data source. You’d probably want a mini-DSL for various source formats and transforming them into your target representation. This also works great when you’ve picked manual inputs, but exactly specifying the output result is a pain because it is large and complicated. This is data-driven testing.
Non-fuzzing testing frameworks like Quickcheck and Smallcheck are reasonably good at dealing with runtime exceptions but not so much with more critical failures like segmentation faults. Drivers for these frameworks should take advantage of statelessness to notice when their runner has mysteriously died and let the user know the minimal invocation necessary to reproduce the crash—with this modification, these frameworks subsume fuzzers (which are currently built in an ad hoc fashion.)

It would be great if we didn’t have to commit to one testing methodology, and if we could reuse efforts on both sides of the fence for great victory.

ToRA says:

February 22, 2011 at 2:25 am

Full disclosure – this was my PhD, so it’s “research ware”; I’ve worked on a Haskell testing tool that sits in the more-automated side, that can do runtime (-segfault), property and cross-checking.

What was interesting was that for cross-checking (testing different implementations), it’s not necessarily the case that taking the inputs used in an old test suite and putting them into a new implementation is the most helpful thing to do. Haskell’s laziness actually opens up a whole world of being able to spot differences in strictness in different implementations. Also LazySmallCheck should be in that picture, leaning towards the ‘faking symbolic execution’ side. (The LSC approach is similar to what my tool does).

http://www.doc.ic.ac.uk/~tora/irulan/

Thomas says:

February 22, 2011 at 10:06 am

I think it’s better to try and prove all the properties (algebraic laws of type class instances like Monads, Applicatives, etc. come to mind) that can be proved with a reasonable amount of work and let those intelligent automated testing tools only loose on those bits that can’t be proved or where formal proof would actually waste more time because you might not care about all the corner cases that you have to look at in the course of a proof development.

I’m writing this mainly because as a side project I’m currently building a small library of type classes modelled after the category theory inspired data structures in Haskell. The purpose is two-fold: First, I cannot stand it when you have obviously trivially provable laws and, yet, do not prove them (or let tools like QuickCheck convince you via intelligent hand waving that your pointed Functor instance adheres to the law). The second reason is that even in the Haskell community people feel that one should reform the hierarchy of type classes such that you develop Monads from Functors or have different additive Monads with different laws to solve the problem that MonadPlus [] might satisfy left distribution, but MonadPlus Maybe does satisfy left catch instead.

Edward Z. Yang says:

February 22, 2011 at 12:06 pm

ToRA: Very cool; I love that you’re doing research into generating strict and lazy data, checking laziness is often that is quite neglected (even though lazy data structures tend to have better theoretical properties.)

Thomas: I absolutely love formal methods (I did intern at Galois for a summer), but the experience has made me keenly aware that proof is just too expensive for many purposes. I do think the Haskell standard libraries would benefit from this treatment. Typeclasses have are not very coherent about what algebraic properties they should satisfy.