DP Zoo Tour
I’ve always thought dynamic programming was a pretty crummy name for the practice of storing sub-calculations to be used later. Why not call it table-filling algorithms, because indeed, thinking of a dynamic programming algorithm as one that fills in a table is a quite good way of thinking about it.
In fact, you can almost completely characterize a dynamic programming algorithm by the shape of its table and how the data flows from one cell to another. And if you know what this looks like, you can often just read off the complexity without knowing anything about the problem.
So what I did was collected up a bunch of dynamic programming problems from Introduction to Algorithms and drew up the tables and data flows. Here’s an easy one to start off with, which solves the Assembly-Line problem:
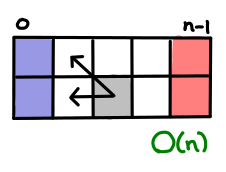
The blue indicates the cells we can fill in ‘for free’, since they have no dependencies on other cells. The red indicates cells that we want to figure out, in order to pick the optimal solution from them. And the grey indicates a representative cell along the way, and its data dependency. In this case, the optimal path for a machine to a given cell only depends on the optimal paths to the two cells before it. (Because, if there was a more optimal route, than it would have shown in my previous two cells!) We also see there are a constant number of arrows out of any cell and O(n) cells in this table, so the algorithm clearly takes O(n) time total.
Here’s the next introduction example, optimal parenthesization of matrix multiplication.
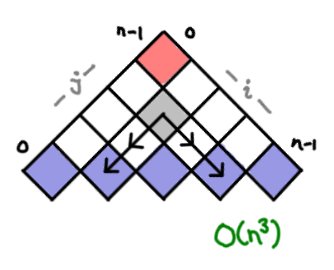
Each cell contains the optimal parenthesization of the subset i to j of matrixes. To figure this out the value for a cell, we have to consider all of the possible combos of existing parentheticals that could have lead to this (thus the multiple arrows). There are O(n²) boxes, and O(n) arrows, for O(n³) overall.
Here’s a nice boxy one for finding the longest shared subsequence of two strings. Each cell represents the longest shared subsequence of the first string up to x and the second string up to y. I’ll let the reader count the cells and arrows and verify the complexity is correct.
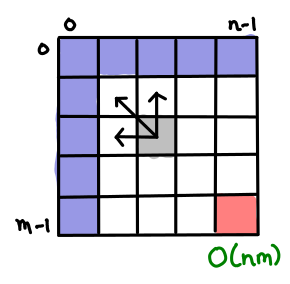
There aren’t that many ways to setup dynamic programming tables! Constructing optimal binary search trees acts a lot like optimal matrix parenthesization. But the indexes are a bit fiddly. (Oh, by the way, Introduction to Algorithms is 1-indexed; I’ve switched to 0-indexing here for my examples.)
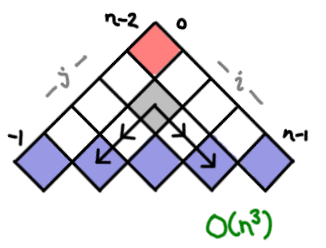
Here we get into exercise land! The bitonic Euclidean traveling salesman problem is pretty well-known on the web, and its tricky recurrence relation has to do with the bottom edge. Each cell represents the optimal open bitonic route between i and j.
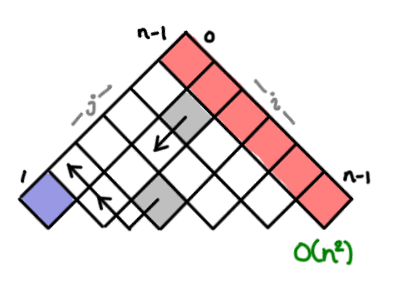
The lovely word wrapping problem, a variant of which lies at the heart of the Knuth TeX word wrapping algorithm, takes advantage of some extra information to bound the number of cells one has to look back. (The TeX algorithm does a global optimization, so the complexity would be O(n²) instead.) Each cell represents the optimal word wrapping of all the words up to that point.
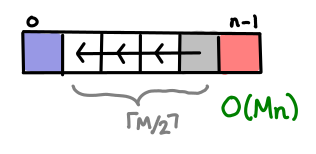
Finally, the edit problem, which seems like the authors decided to pile on as much complexity as they could muster, falls out nicely when you realize each string operation they order you to design corresponds to a single arrow to some earlier cell. Useful! Each cell is the optimal edit chain from that prefix of the source to that prefix of the destination.
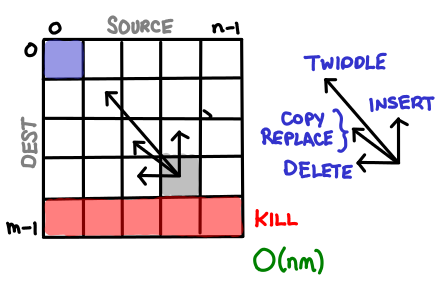
Squares, triangles, rectangles, those were the tables I usually found. I’m curious to know if there are more exotic tables that DP algorithms have filled out. Send them in and I’ll draw them!