Graphs not grids: How caches are corrupting young algorithms designers and how to fix it
Quicksort. Divide and conquer. Search trees. These and other algorithms form the basis for a classic undergraduate algorithms class, where the big ideas of algorithm design are laid bare for all to see, and the performance model is one instruction, one time unit. “One instruction, one time unit? How quaint!” proclaim the cache-oblivious algorithm researchers and real world engineers. They know that the traditional curriculum, while not wrong, is quite misleading. It’s simply not enough to look at some theoretical computing machine: the next-generation of high performance algorithms need to be in tune with the hardware they run on. They couldn’t be more right.

Last Friday, Dr. John Feo gave a Galois Tech Talk entitled Requirements and Performance of Data Intensive, Irregular Applications (slides 1). However, Feo also brought in some slides from another deck which talked more generally about the Center for Adaptive Supercomputing Software (slides 2). The resulting presentation was a blend of the principles of massively multithreaded processor architectures—specifically the Cray XMT —and practical engineering problems encountered when writing software for such machines. Since I can’t resist putting spin on a good presentation, the title of these notes comes from a conversation I had with Feo after the tech talk; I don’t mean to demean those doing research on traditional processor, just to suggest that there is another approach that doesn’t receive as much attention as Feo thinks it should. For those of you who like puzzles, there will also be a “Why does this deadlock?” question at the end of this post.
Graphs not grids. John Feo started off by distinguishing between problems in science and problems in informatics. Scientific problems frequently take the form of grids, slowly evolving systems that exhibit the principle of locality and involve only nearest neighbor communication inside the grid. These types of problem are tackled extremely well by cluster parallelization: planar grids are obvious to partition, and nearest neighbor communication means that the majority of any computation will be local to the node containing the partition. Locality also means that, with a little care, these algorithms can play nicely with the CPU cache: for cache-oblivious algorithms, this just means partitioning the problem until it fits on-board.
Data informatics, however, sees quite different datasets. Consider the friends graph on Facebook, or the interlinking pages of the web, or the power grid of your country. These are not grids (not even the power grid): they are graphs. And unlike a quantum chromodynamic simulation, these graphs are dynamic, constantly being changed by many autonomous agents, and they can present some unique problems for traditional processors and parallelization.
Difficult graphs. There are several types of graphs that are particularly hard to run algorithms on. Unfortunately, they also tend to show up frequently in real world datasets.
Low diameter (aka “small world”) graphs are graphs in which the degree of separation between any two nodes is very low. The work necessary on these graphs explodes; any algorithm that looks at the neighbors of a node will quickly find itself having to operate on the entire graph at once. Say good bye to memory locality! The tight coupling also makes the graph difficult to partition, which is the classic way to parallelize a computation on a graph.
Scale-free graphs are graphs in which a small number of nodes have an exponentially large number of neighbors, and a large number of nodes have a small number of neighbors. These graphs are also difficult to partition and result in highly asymmetric workloads: the few nodes with large amounts neighbors tend to attract the bulk of the work.
There are also properties of graphs that can make computation more difficult. Non-planar graphs are generally harder to partition; dynamic graphs have concurrent actors inserting and deleting nodes and edges; weighted graphs can have pathological weight distributions; and finally graphs with typed edges prevent you from reducing a graph operation into a sparse matrix operation.
This slide from Feo sums up the immediate effects of these types of graphs nicely.

Multithreaded processors: gatling guns of the computing world. The gatling gun was one of the first well-known rapid-fire guns. Other guns simply increased their rate of fire, but quickly found that their gun barrels overheated if they attempted to fire too quickly. The gatling gun used multiple barrels, each of which individually fired at a slower rate, but when rotated in succession allowed a continuous stream of bullets to be fired while allowing the barrels not in use to cool off.
The time it takes for a discharged barrel to cool off is similar to the latency of a memory access. Since memory accesses are expensive, traditional processors try to “use less bullets” and forgo memory accesses with on-processor caches. However, a massively multithreaded processor takes a different approach: instead of trying to eliminate the memory latency, it simply hides it by context switching away from a thread that requests memory, so that by the time it switches back, the access has been completed and the data available. No need to twiddle your thumbs while waiting for data; go do something else! On specialized hardware, the researches at PNNL have been able to get processor utilization upwards of 90%; on less specialized hardware, performance targets are a bit more modest—40% or so.
Implications. Because the massively multithreaded processor is hiding memory access latency, not trying to get rid of it, traditional constraints such as memory locality become unimportant. You don’t need data to be near your computation, you don’t need to balance work across processors (since it all goes into threads that cohabit), you don’t need to handle synchronization like a time bomb. What you learned in undergraduate computer science is relevant again! In Feo’s words:
- Adaptive and dynamic methods are okay,
- Graph algorithms and sparse methods are okay, and
- Recursion, dynamic programming, branch-and-bound, dataflow are okay!
Your hardware, then, will be tailored for graph-like computations. This includes a huge global address space to shove your graph into, extremely lightweight synchronization in the form of full/empty bits (Haskell users might recognize them as extremely similar to MVars; indeed, they come from the same lineage of dataflow languages) and hardware support for thread migration, to balance out workloads. It’s something of a holy hardware grail for functional languages!
The Cray XMT is one particular architecture that John Feo and his fellow researchers have been evaluating. It easily beats traditional processors when handling algorithms that exhibit poor locality of reference; however, it is slower when you give the traditional processor and algorithm with good locality of reference.
Maximum weight matching. There are many graph problems—shortest path, betweenness centrality, min/max flow, spanning trees, connected components, graph isomorphism, coloring, partitioning and equivalence, to name a few. The one Feo picked out to go into more detail about was maximum weight matching. A matching is a subset of edges such that no two edges are incident on the same vertex; so a maximum weight matching is a matching where the weights of the selected edges has been maximized (other cost functions can be considered, for example, on an unweighted graph you might want to maximize the number of edges).
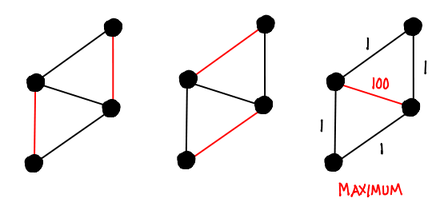
While there is a polynomial-time algorithm for finding maximum weight matchings, we can get an approximate answer more quickly with a greedy parallel algorithm called Hoepman’s algorithm. It is reminiscent of the stable marriage (Gale-Shapely) algorithm; the algorithm runs as follows: each node requests to be paired with the node across most expensive vertex local to it. If two nodes request each other, they are paired, and they reject all other pairing requests. If a node gets rejected, it tries the next highest vertex, and so on. Since a node will only accept one pairing request, edges in the pairing will never be incident on the same vertex.
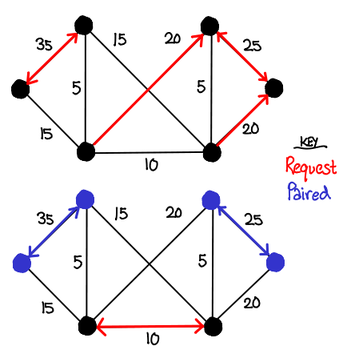
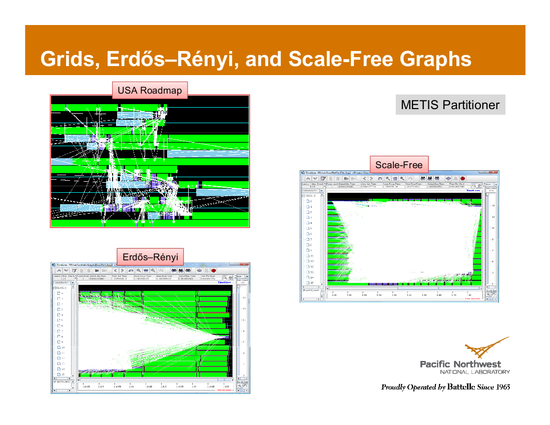
Hoepman’s algorithm relies on a theoretical machine that is able to allocate a processor per node. This doesn’t bode well for traditional cluster machines, so Halappanavar, Dobrian and Pothen proposed a parallel version that separates the graph into partitions which are given to processors, and uses queues to coordinate communicate across the partitions. Unfortunately, this approach performs extremely poorly in some cases. Feo has some visualizations of this phenomenon: the pictures below are visual depictions of processor cores, where green indicates the core is busy, and white lines indicate inter-processor communication. While the regular, planar graph of US roadways handles the problem nicely, both graphs generated by the Erdős–Rényi model and scale-free free graphs (one of the “tough” graph types we mentioned earlier) have inter-processor communication explode in sheets of white.
Machines like the Cray XMT, however, make it plausible to try to implement Hoepman’s original algorithm more closely. Give each node a thread, and implement the algorithm as described.
In order to implement signaling, we can use the full/empty bit primitive. Every edge has two full/empty bits, each endpoint owning one each. When a node attempts to pair with a vertex, it fills its own bit with 1, and then tries to read the other bit. While the bit is empty, the node’s thread blocks. If the other bit reads 1, the node is paired: fill all other bits the node owns with 0 and then terminate. If the other bit reads 0, try your next neighbor with the highest edge.
This approach doesn’t quite work, due to real-world constraints on the Cray XMT. In particular, for large graphs, it’s not possible for every thread to be run simultaneously; only a subset of nodes can be run at a time. If it just happens that every node is waiting on another node which is not being currently run, all the nodes block, and we have deadlock. In particular, the Cray XMT will not pre-empt a thread that is blocked by default, because the cost of context switching is so high. (You could turn pre-emption on, in which case this deadlock would go away, but at great cost to runtime. While the Cray does thread-level context switching every cycle, actually evicting the thread off its processor is quite expensive.)
The simple fix Feo applied was the following observation: as long as we schedule nodes closed to expensive edges, there will always be work to be done: in particular, the two nodes incident to the most expensive unpaired edge will always be able to pair. So sort the nodes in order of their most expensive vertex, and then run the algorithm. This resolved most of the deadlocks.
Ending notes. While massively multithreaded architectures are promising, there is a lot of work that still needs to be done both on the hardware side (making this technology available on commodity hardware, and not just the Cray XMT) as well as the software ecosystem (building new programming APIs to take advantage of the architecture.) Even further, the problems in this domain are so diverse that no one machine can truly attack all of them.
Nevertheless, Feo remains optimistic: if the problems are important enough, the machines will get built.
Puzzle. Even with the sorting modification, the implementation of maximum matching on the Cray XMT with preempting disabled still deadlocks on some large graphs. What graphs cause it to deadlock, and what is an easy way to fix the problem? (According to Feo, it took him three days to debug this deadlock! And no, turning on preemption is not the answer.) Solution will be posted on Friday.
(There might be answers in the comment section, so avert your eyes if you don’t want to be spoiled.)
Update. I’ve removed the link to the CACM article; while I thought it was timely for Reddit readers, it implied that Varnish’s designer was a “young algorithms designer corrupted by cache locality”, which is completely false. The expression was meant to express Feo’s general dissatisfaction with the general preoccupation of the algorithms community towards the complicated cache-aware/oblivious algorithms, and not directed at anyone in particular.