“Roughing it,” so to speak.

With no reservations and no place to go, the hope was to crash somewhere in the Jungfrau region above the “fogline”

but these plans were thwarted by my discovery that Wengen had no hostels. Ah well.



Still pretty.
Of which I do not have a photo, one of the astonishing sights from Lauterbrunnen at night (I checked in and asked the owner, “Any open beds?” They replied, “One!” Only one possible response: “Excellent!”) is that the towns and trains interspersed on the mountains almost look like stars (the mountain hidden from view, due to their sparseness), clustered together in chromatic galaxies.
Read more...
New to this series? Start at the beginning!
Recursion is perhaps one of the first concepts you learn about when you learn functional programming (or, indeed, computer science, one hopes.) The classic example introduced is factorial:
fact :: Int -> Int
fact 0 = 1 -- base case
fact n = n * fact (pred n) -- recursive case
Recursion on natural numbers is closely related to induction on natural numbers, as is explained here.
Read more...
How do you decide what to work on? I started thinking about this topic when I was wasting time on the Internet because I couldn’t think of anything to do that was productive. This seemed kind of strange: there were lots of things I needed to do: vacations to plan, projects to work on, support requests to answer, patches to merge in, theorems to prove, blog posts to write, papers to read, etc. So maybe the problem wasn’t that I didn’t have anything to do, it was just that I had too much stuff to do, and that I needed to pick something.
Read more...
I will be in the following places at the following times:
- Paris up until evening of 12/22
- Berlin from 12/23 to 12/24
- Dresden on 12/24
- Munich from 12/25 to 12/26
- Zurich on 12/27
- Lucerne from 12/28 to 12/29
Plans over the New Year are still a little mushy, so I’ll post another update then. Let me know if you’d like to meet up!
Non sequitur. I went to the Mondrian exhibition at Centre Pompidou, and this particular gem, while not in the exhibition itself (it was in the female artists collection), I couldn’t resist snapping a photo of.
Read more...
What semantics has to say about specifications
Conventional wisdom is that premature generalization is bad (architecture astronauts) and vague specifications are appropriate for top-down engineering but not bottom-up. Can we say something a little more precise about this?
Semantics are formal specifications of programming languages. They are perhaps some of the most well-studied forms of specifications, because computer scientists love tinkering with the tools they use. They also love having lots of semantics to pick from: the more the merrier. We have small-step and big-step operational semantics; we have axiomatic semantics and denotational semantics; we have game semantics, algebraic semantics and concurrency semantics. Describing the programs we actually write is difficult business, and it helps to have as many different explanations as possible.
Read more...
In which Edward travels France
Many, many years ago, I decided that I would study French rather than Spanish in High School. I wasn’t a particularly driven foreign language learner: sure I studied enough to get As (well, except for one quarter when I got a B+), but I could never convince myself to put enough importance on absorbing as much vocabulary and grammar as possible. Well, now I’m in France and this dusty, two-year old knowledge is finally being put to good use. And boy, am I wishing that I’d paid more attention in class.
Read more...
New to this series? Start at the beginning!.
Today we’re going to take a closer look at a somewhat unusual data type, Omega. In the process, we’ll discuss how the lub library works and how you might go about using it. This is of practical interest to lazy programmers, because lub is a great way to modularize laziness, in Conal’s words.
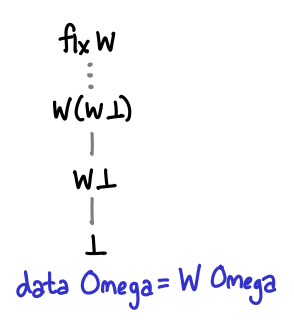
Omega is a lot like the natural numbers, but instead of an explicit Z (zero) constructor, we use bottom instead. Unsurprisingly, this makes the theory easier, but the practice harder (but not too much harder, thanks to Conal’s lub library). We’ll show how to implement addition, multiplication and factorial on this data type, and also show how to prove that subtraction and equality (even to vertical booleans) are uncomputable.
Read more...
Previously, we’ve drawn Hasse diagrams of all sorts of Haskell types, from data types to function types, and looked at the relationship between computability and monotonicity. In fact, all computable functions are monotonic, but not all monotonic functions are computable. Is there some description of functions that entails computability? Yes: Scott continuous functions. In this post, we look at the mathematical machinery necessary to define continuity. In particular, we will look at least upper bounds, chains, chain-complete partial orders (CPOs) and domains. We also look at fixpoints, which arise naturally from continuous functions.
Read more...
Between packing and hacking on GHC, I didn’t have enough time to cough up the next post of the series or edit the pictures for the previous post, so all you get today is a small errata post.
- The full list diagram is missing some orderings: ★:⊥ ≤ ★:⊥:⊥ and so on.
- In usual denotational semantics, you can’t distinguish between ⊥ and
λ_.⊥. However, as Anders Kaseorg and the Haskell Report point out, with seq you can distinguish them. This is perhaps the true reason why seq is a kind of nasty function. I’ve been assuming the stronger guarantee (which is what zygoloid pointed out) when it’s not actually true for Haskell. - The “ought to exist” arrow in the halts diagram goes the wrong direction.
- In the same fashion of the full list diagram,
head is missing some orderings, so in fact they gray blob is entirely connected. There are situations when we can have disconnected blobs, but not for a domain with only one maximum. - Obvious typo for fst.
- The formal partial order on functions was not defined correctly: it originally stated that for f ≤ g, f(x) = g(x); actually, it’s weaker than that: f(x) ≤ g(x).
- A non-erratum: the right-side of the head diagram is omitted because… adding all the arrows makes it look pretty ugly. Here is the sketch I did before I decided it wasn’t a good picture.

Read more...
Gin, because you’ll need it by the time you’re done reading this.
Last time we looked the partial orders of values for data types. There are two extra things I would like to add: an illustration of how star-subscript-bottom expands and an illustration of list without using the star-subscript-bottom notation.
Here is a triple of star-subscript-bottoms expanded, resulting in the familiar Hasse diagram of the powerset of a set of three elements ordered by inclusion:
Read more...






