May 5, 2010Attention Conservation Notice. Unqualified identifiers that are used the most on Hackage.
Perhaps you dread the error message:
Ambiguous occurrence `lookup'
It could refer to either `Prelude.lookup', imported from Prelude
or `Data.Map.lookup', imported from Data.Map
It is the message of the piper that has come to collect his dues for your unhygenic unqualified unrestricted module import style.
Or perhaps your a library writer and trying to think up of a new symbol for your funky infix combinator, but you aren’t sure what other libraries have used already.
I took the archive (TAR) of the latest Hackage packages for everything, whipped up a script to extract all unqualified names exported by public modules, and then counted up the most used.
Disclaimer. Data constructors and record fields, unless they were explicitly exported, are not included in this count. I also don’t count modules that export everything from the global namespace because they omitted a list of names to export. Counts are per module, and not per package. CPP and HSC files were not counted, due to limitations of haskell-src-exts.
Top twenty identifiers (as of September 2, 2012).
106 empty
69 insert
69 toList
66 fromList
56 null
54 singleton
44 run
42 encode
41 decode
41 delete
39 size
37 theModule
35 member
32 parse
31 get
30 lookup
30 union
29 Name
29 space
28 Node
Top twenty infix operators (as of September 2, 2012).
25 !
19 <>
17 <+>
14 </>
11 <$>
10 //
10 ><
9 .:
9 <$$>
9 ∅
8 &
8 .=
8 <?>
8 <||>
8 \\
8 |>
7 #
7 $$
7 *.
7 <->
The exclamation mark has earned the reputation as an “indexing” operator, and unsurprisingly is at the top. I hear from Edward Kmett that <> is making its way into the base as mappend, which is welcome, although might suck for the other six modules which redefined it for their own nefarious purposes.
All infix operators, sorted by usage and then lexicographically (as of September 2, 2012).
! <> <+> </> <$> // >< .: <$$> ∅ & .= <?> <||> \\ |> # $$ *. <-> <. <//>
<| <|> ==> >. ||. ∈ ∉ !! &&. ++ +++ /=. <=. =: ==. >=. ∋ ∌ ∩ ∪ .|. :->
<: ? ∆ ∖ .&. .* .-. <&> <.> << === ?? @@ \/ ^^ |+ |- ||| ~~ !!! !> !? ##
$+$ += +> -<- .*. .:? .<. .==. .>. /=? /\ :- :> :~> <$?> <+< <=> <=? <?
<|?> =. ==? =~ >-> >=? >? @# ^ ~> ¬ ∘ ∧ ∨ ≡ ≢ ⊂ ⊃ ⊄ ⊅ ⊆ ⊇ ⊈ ⊉ !: $# $>
$~ % %> && &&? &= ** *|* + --> ->- -| . .!= .!=. .&&. .&.? .*> .+ .++.
.+. ... ./. ./\. .:: .<=. .=. .=> .>=. .\/. .| .||. :* :+ :. := :=: <*.
<*> <++ <++> <..> <:> <<|> <== <|*|> =$= >+> >=> >>>= >|< ?> ?>= @@@ ^#
^$ ^: ^^^ |* || ||* ||+ ||? ~: ~? ≠ ≮ ≯ ⊕ ⧺ !$ !$? !. !=. !>>= #! #!!
#~~ $ $! $$$ $$$? $$+ $$++ $$+- $$= $- $. $.// $/ $// $= $=! $? $| $~!
%% %&& %+ %/= %: %< %<= %== %>= %|| &#& &&& &+ &. &.// &/ &// &=# &> &@
&| * *! *& *&&&* *&* ***** ****/* ****/*** ****//* ****//*** ****|*
****|*** ****||* ****||*** ***/* ***/** ***/**** ***//* ***//**
***//**** ***|* ***|** ***|**** ***||* ***||** ***||**** **. **/* **/***
**//* **//*** **> **|* **|*** **||* **||*** */* */** */*** */**** *//*
*//** *//*** *//**** *<<<* *=* *=. *=>* *> *>>>* *? *@ *^ *|** *|***
*|**** *||* *||** *||*** *||**** +% ++. ++> ++>> ++@ +/+ +: +:+ +=. +>>
+@ +^ +| - -!- -$ -->> -/\- -: -< -<< -<=- -=. -=> ->> -?- -?-> -?> -?>>
-@ -\/- -^ -|- -~> .! .# .$. .- .--. .->. .... ./ ./= ./=. .:. .::: .<
.<<. .<= .== .>>. .@ .@$ .@~ .\. .|| .~ .~. / /+/ /- /. /<-. /=: />/ /^
/| /~ /~? :*: :+: :-: :<-> :<: :<=: :<> :<~> :=+ :><: :~ <! <#$> <$| <%
<&&> <* <+ <-$ <-- <-. <-: </=? <<! <</ <<: <<< <<? <<\ <<| <<~ <=! <=:
<==? <=@ <=@@ <>>= <?< <??> <@ <@> <@@ <~ =$ =$$= =*= =/= =< =<< =<<!
=<<< =<= =<>= =<? ==! =>> =~= =≪ >! >$$< >$< >*> >-- >-< >: >:> >=! >=:
>== >===> >=>=> >=@ >=@@ >> >>-> >>. >>= >>=# >>== >>=\/ >>=|\/ >>=||
>>=||| >>> >>@ >?> >@ >@@ >||< ?! ?+ ?/= ?: ?< ?<= ?= ?== @! @= @==? @=?
@? @?= @?== \== ^% ^-^ ^. ^>>= ^@ ^^. |#| |$> |*| |-> |-| |. |/ |// |:
|<- |= |=> |=| |? |@ |\ |\\ |||| ~/= ~== ~=? ~?= ~|||~ ~||~ ~|~ ~~# ~~>
~~? ~~~> · ·× × ×· ÷ ⇒ ⇔ ∀ ∃ ≫ ≫= ⊛ ⊥ ⊨ ⊭ ⊲ ⊳ ⋅ ⋈ ⋘ ⋙ ▷ ◁ ★
It’s a veritable zoo! (I’m personally reminded of Nethack.)
Source. The horrifying code that drove this exercise can be found at Github. I used the following shell one-liner:
for i in *; do for j in $i/*; do cd $j; tar xf *.tar.gz; cd ../..; done; done
to extract all of the tarballs inside the tar file.
Postscript. It would be neat if someone could fix the discrepancies that I described earlier and do a more comprehensive/correct search over this space.
May 3, 2010Attention Conservation Notice. A listing of how Gang of Four design patterns might be equivalently implemented in Haskell. A phrasebook for object-oriented programmers dealing with functional programming concepts.
In their introduction to seminal work Design Patterns, the Gang of Four say, “The choice of programming language is important because it influences one’s point of view. Our patterns assume Smalltalk/C++-level language features, and that choice determines what can and cannot be implemented easily. If we assumed procedural languages, we might have included design patterns called ‘Inheritance,’ ‘Encapsulation,’ and ‘Polymorphism.’”
What is easy and what is hard to implement in a functional programming language? I decided to revisit all 23 original Gang of Four design patterns under that lense. My hope is that these results will be useful to Object Oriented Programmers seeking to learn the ways of Functional Programming.
Strategy. First class functions and lambdas. Any extra data that might be placed as class members is traditionally implemented using closures (which stash the data in a lambda function’s environment) or currying (which create implicit closures for function’s arguments). Strategies are also powerful because they are polymorphic; type synonyms for function types can play a similar role. Java has recognized anonymous functions as a good idea, and have added facilities for anonymous classes, which are frequently used in this capacity.
Factory Method and Template Method. Higher-order functions. Instead of making a subclass, just pass the the function you’d like to vary the behavior of with the function.
Abstract Factory, Builder and Bridge. Type classes and smart constructors. Type classes are capable of defining functions which creating instances of themselves; all a function needs to do to take advantage of this is to commit itself to returning some value of type TypeClass a => a and using only (constructor et alia) functions that the type class exposes. If you’re not just constructing values but manipulating them with the general type class interface, you have a Bridge. Smart constructors are functions built on top of the basic data constructor that can do “more”, whether this is invariant checking, encapsulation or an easier API, this can correspond to more advanced methods that a factory provides.
Adapter, Decorator and Chain of Responsibility. Composition and lifting. Function composition can be used to form a pipeline of data between functions; a foreign function can be sandwiched between two functions that convert to and from the type the function expects, or a function can be composed with another to make it do more things. If the signature stays the same, one or more of the functions was endomorphic. If the functions have side effect, it may be Kleisli arrow composition (more plainly spoken as monadic function composition.) Multiple functions can handle the same input using the Reader monad.
Visitor. Equational functions. Frequently foldable. Many functional languages favor grouping the same operation on different data constructors together, in a mathematical equational style. This means similar behaviors are grouped together. Traditional grouping of behavior by “class” is implemented with type classes. Visitors typically collapse the data structures they operate on into smaller values, this is seen in the fold family of functions.
Interpreter. Functions. Frequently circumvented with an embedded domain specific language. Algebraic data types make light-weight abstract syntax trees easy to formulate. Just as Visitor is often used with Interpeter, you’ll probably write your interpreting functions with pattern matching. Even better, don’t come up with another data type; just use functions and infix operators to say what you mean. Closely related to…
Command. Monads. See also algebraic data types, frequently generalized (GADT). A pure language will not run your IO until main touches it, so you can freely pass values of type IO a without fear of actually causing the side-effect, though these functions are difficult to serialize (a common motivation behind Command). Parametrization of the action to perform is once again achieved through higher-order functions. GADTs are a little more bulky, but can be seen in places like the Prompt monad (PDF), where a GADT is used to represent actions that another function interprets into the IO monad; the type gives a statically enforced guarantee of what operations in this data type are allowed to do.
Composite. Recursive algebraic data types. Especially prominent since there’s no built-in inheritance.
Iterator. Lazy lists. Iterators expose an element-by-element access of a data structure without exposing it’s external structure; the list is the API for this sort of access and laziness means we don’t compute the entirety of the stream until it is necessary. When IO is involved, you might use a real iterator.
Prototype. Immutability. Modification copies by default.
Flyweight. Memoising and constant applicative forms (CAF). Instead of calculating the result of an expression, create a data structure that contains all of the results for all possible input values (or perhaps, just the maximum memo). Because it is lazy, the result is not computed until it is needed; because it is a legitimate data structure, the same result is returned on successive computations. CAFs describe expressions that can be lifted into the top-level of a program and whose result can be shared by all other code that references it.
State and Memento. Unnecessary; state has an explicit representation and thus can always be arbitrarily modified, and it can include functions, which can be changed to change behavior. State as a function (rather than an object or an enumeration), if you will. The encapsulation provided by Memento is achieved by hiding the appropriate constructors or destructors. You can easily automatically manage past and future states in an appropriate monad such as the Undo monad.
Singleton. Unnecessary; there is no global state except in a monad, and the monad’s type can enforce that only one instance of a record is present; functions exist in a global namespace and are always accessible.
Facade. Functions. Generally less prevalent, since function programming focuses on input-output, which makes the straight-forward version use of a function very short. High generality can require more user friendly interfaces, typically implemented with, well, more functions.
Observer. One of many concurrency mechanisms, such as channels, asynchronous exceptions and mutable variables. See also functional reactive programming.
Proxy. Wrapped data types, laziness and garbage collector. See also ref monadic types (IORef, STRef), which give more traditional pointer semantics. Laziness means structures are always created on demand, garbage collection means smart references are not necessary. You can also wrap a data type and only publish accessors that enforce extra restrictions.
Mediator. Monad stacks. While it’s not useful to talk about interactions between objects, due to a preference for stateless code, monad stacks are frequently used to provide a unified interface for code that performs operations in a complex environment.
Comments and suggestions appreciated; I’ll be keeping this post up-to-date.
April 30, 2010I was in rehearsal today, doodling away second oboe for Saint Saens’ Organ Symphony for the nth time, and it occurred to me: I’ve listened to and played this piece of music enough times to know the full overall flow as well as a good chunk of the orchestral parts, not just mine. So when the hymnal calls give way to the triumphant entrance of the organ in the last movement, or when the tempos start shifting, simultaneously speeding up and slowing down, at the end of the piece, it’s not surprising; it’s almost inevitable. Couldn’t have it any other way.
But we could have had it another way; Saint Saens could have decided that he wanted to move around the second movement or introduce another theme or any other multitude of changes. But he composed this piece, and this piece alone, and that is what has been enshrined as beauty.
And it got me thinking about the first problem on my computability problem set, which asked me to show a fundamental truth of the universe (well, within the boundaries of the math philosophers); nonnegotiable, unmoving, universal. Or the programs I write, certainly a creative process but firmly anchored to the tangible realm via requirements and specifications. How creative those mathematicians and programmers needed to be to craft elegant proofs and programs, and yet how far away from artists they yet are.
Non sequitur. MIT/GNU Scheme loves spewing out lots of extra banner crud when you run it, even when you don’t actually want to use the interactive REPL and just run some mit-scheme code. As it turns out, the maintainer of mit-scheme made the following decision:
In the past my (CPH) policy for a stable release was that the documentation had to be updated for the release before it went out. In practice, this has meant that there have been no stable releases in recent years. As of this release, we will no longer consider updated documentation a prerequisite for a stable release.
Uh, what?
Anyway, there’s this wonderful undocumented option named --batch-mode which suppresses entry messages. However, in 7.7.90 (default in Ubuntu Karmic, and don’t you dare try compiling it yourself; you need mit-scheme to compile mit-scheme), it doesn’t suppress the “Loading…” messages, so you need to invoke load with the following hack:
# run-scheme LOAD EVAL
# LOAD - Scheme file to load
# EVAL - Scheme expression to evaluate
run-scheme() {
# --batch-mode doesn't work completely on mit-scheme 7.7.90, in
# particular it fails to suppress Loading... messages. As a result,
# we require this elaborate work-around.
mit-scheme --batch-mode --eval \
"(begin (set! load/suppress-loading-message? #t) \
(load \"$1\") $2)" </dev/null
}
It’s, to put it lightly, kind of disappointing.
April 28, 2010Last time I did an Inessential guide to data-accessor and everyone told me, “You should use fclabels instead!” So here’s the partner guide, the inessential guide to fclabels. Like data-accessor the goal is to make record access and editing not suck. However, it gives you some more useful abstractions. It uses Template Haskell on top of your records, so it is not compatible with data-accessor.
Identification. There are three tell-tale signs:
- Type signatures that contain
:-> in them (“Oh, that kind of looks like a function arrow… but it’s not? Curious!”), - Records that contain fields with a leading underscore (as opposed to data-accessor’s convention of an trailing underscore), and
- An
import Prelude hiding (id, (.), mod), with an import from Control.Category to replace them.
Interpreting types. A label is signified by r :-> a which contains a getter r -> a and a setter a -> r -> r. Internally, a wrapped label is simply a point, a structure consisting of r -> a and b -> r -> r, with a required to be equal to b. (As we will see later, a point is useful in its own right, but not for basic functionality.)
Accessing record fields.
get fieldname record
Setting record fields.
set fieldname newval record
Modifying record fields. For fieldname :: f a :-> a, modifier should have type a -> a.
mod fieldname modifier record
Accessing, setting and modifying sub-record fields. Composition is done with the period operator (.), but you can’t use the one from the Prelude since that only works with functions. The composition is treated as if you were you composing the getter.
get (innerField . outerField) record
set (innerField . outerField) newVal record
mod (innerField . outerField) modifier record
Accessor over applicative. You can use fmapL to lift an accessor into an applicative context. This is useful if your record is actually Maybe r (You can turn r :-> a into Maybe r :-> Maybe a).
But wait, there’s more!
More fun with views. Remember that a point is a getter and a setter, but they don’t have to be for the same types. Combined with a clever applicative instance, we can use this to incrementally build up a label composed of multiple labels. The result looks a lot like a view that you’d be able to create on a relational database. The recipe is:
- Have the constructor for the resulting type (e.g.
(,), the tuple constructor), - Have all of the accessors for the resulting type (e.g.
fst and snd), and - Have the labels you would like to compose together (say,
label1 and label2).
Combine, with for, each accessor for the resulting type (2) with the label to be accessed with that accessor (3), combine all of these resulting points with the constructor for the resulting type with the applicative instance, i.e. <$> and <*>, and then stick it in a label with Label:
(,) <$> fst `for` label1 <*> snd `for` label2
Amazingly, you won’t be able to mix up which argument an accessor (2) should be placed in; the result won’t typecheck! (See the Postscript for a more detailed argument.)
More fun with lenses. A function implies directionality: a to b. But light can filter through a lense either way, and thus a lense represents a bidirectional function. We can apply filter a label f :-> a through a lense a :<->: b to get a new label f :-> b (remember that composition with a regular function is insufficient since we need to put values in as well as take values out). One has to be careful about what direction your lense is pointed. If label :: r :-> a, in :: b -> a and out :: a -> b, then:
(out <-> in) `iso` label :: r :-> b
(in <-> out) `osi` label :: r :-> b
The other directions won’t typecheck if a != b.
You can lift a lense into a functor using lmap (it simply runs fmap on both directions).
Further reading. The Hackage documentation has a ton of excellent examples.
Postscript. With our original example in mind:
label1 :: r -> a
label2 :: r -> b
(,) <$> fst `for` label1 <*> snd `for` label2 :: r :-> (a, b)
We consider the types of the points we’ve constructed, before combining them with the applicative instance:
fst `for` label1 :: Point Person (a, b) a
snd `for` label2 :: Point Person (a, b) b
We have a shared applicative functor Point Person (a, b), and if we treat that as f, clearly:
(,) :: a -> b -> (a, b)
fst `for` label1 :: f a
snd `for` label2 :: f b
(,) <$> fst `for` label1 <*> snd `for` label2 :: f (a, b)
which is equivalent to Point Person (a, b) (a, b), which is a valid Label.
But what is for doing? The source code documentation says:
Combine a partial destructor with a label into something easily used in the applicative instance for the hidden Point datatype. Internally uses the covariant in getter, contravariant in setter bi-functioral-map function. (Please refer to the example because this function is just not explainable on its own.)
Well, I’m going to ignore this advice, since you’ve seen the example already. Let’s parse this. for is covariant in getter r -> a and contravariant in setter a -> f -> f. These terms are from category theory describing functors. A covariant functor is a “normal” functor, whereas a contravariant functor is one with composition flipped around. So while normally fmap f g == f . g, in the contravariant world fmap f g == g . f:
for :: (i -> o) -> (f :-> o) -> Point f i o
for a b = dimap id a (unLabel b)
Well, we’re not doing much interesting to the getter, but we’re mapping a :: (a, b) -> a (in our example) onto the setter a -> f -> f. Luckily (for the befuddled), the covariant map doesn’t typecheck ((a, b) != (f -> f)), but the contravariant map does: (a, b) -> f -> f, which is a new setter that takes (a, b), precisely what we expected from the type signature.
So, for sets up our setters and partially our getter, and the applicative instance finishes setting up our getter.
April 26, 2010Tagline: Assertions considered not ideal.
I think automated tests are great. I used two particular flavors of test, the unit test and the integration test, extensively in HTML Purifier and they’re the only reason why I feel comfortable making changes to code that I first wrote in High School. The automated tests let me hack and then figure out if I broke anything with the single stroke of a button, rather than manually shove a few inputs in and see if they “look alright.” They’re also an informal specification of “what I wanted the code to do” when I originally wrote it, by the fine tradition of an example.
Both unit tests and integration tests were built on top of the SimpleTest “unit testing” library. I place the “unit testing” in quotes because, while SimpleTest is great for unit testing (the testing of individual components), it also can be used for integration testing (the testing of multiple components together) and system testing (the entire system, for web applications this commonly involves writing scripts to navigate the website); in fact, it has facilities in place to make the latter two easier to do!
Perhaps a more accurate description of SimpleTest as a whole is that it is a descendant of the xUnit testing framework. You know, the “make a test function that sets some stuff up, runs some code, and makes some asserts” style of testing. The idea of an assertion is essential; sans exception handling, that’s your single portal into whether or not the test code failed or succeeded.
I was writing some tests in JUnit the other day, and it reminded me a little bit why, even though automated tests are great, I’m somewhat reluctant to roll them out in the first place. They’re so verbose! Every test method I have to instantiate whatever class I want, do whatever initialization I need to it, create my input data (if I’m directly building it with new, this can easily take several lines), run the function, and then test if the output data is what I expected (either by laborious poking at the various fields and methods in it or, if I had the foresight to implement equality, construct the expected output result and compare them.) “But wait,” you say, “that’s precisely what setUp and tearDown are for!” and then you move chunks of this code into those methods, but the substantial bits of boilerplate for creating inputs and verifying results remain, and you are terrified of abstracting over them because adding more code means there’s more chance for your test to be wrong!
But there’s not a good way out of this mess, because the list of function calls to the unit under test is truly the “input” to your test suite, and then list of expressions passed into the assertions is truly the “output” of your test suite. The particular assertion you choose to use is the “expected value” of your test suite. So why does it feel like boilerplate?
Maybe because the model of setUp and tearDown methods and test methods and assertions is the wrong one for many types of code: the correct model is the input value, output value and expected value model! And for pure code, the code that actually has a more refined notion of its input and its output than “a code listing” and “the global state of the application after you ran the code listing”; maybe it truly is just “two integers” and “an integer.” And then, the test code you write should actually reflect that!
So how do we make this happen? You want a DSL. Some languages are strong enough that you can get away with an embedded DSL of sorts. But many languages make this too cumbersome, so they invent their own test format and write the necessary boilerplate code to parse it and marshal it around. Obviously there need to be enough tests of this form to make writing all of this infrastructure worthwhile, and so when that’s not true people fall back to the quick and dirty xUnit style of testing. But by doing this, you’ve obscured the shape of your test, and since “quick and dirty” never means “ephemeral”, your test suite grows and grows and you never end up cutting over to the right way. Ever.
At this point, it’s about time for a little Haskell advocacy. How can you make your tests lest cumbersome from the get go? Use a language that encourages the construction mini-DSLs. Haskell has flexible syntax and type facilities to make this doable, check. Use a language that encourages you to think carefully about functions, which have clear inputs and outputs, not classes and methods and mutable state. Haskell is a functional programming language, check. Use a language in which abstraction is cheap and boilerplate is killed with fire. Haskell, check. Use a language that, once you’ve gotten tired of writing input and output values over and over again, and not the boilerplate of an entire xUnit test case, gives you the rope to automate that process too! QuickCheck and Haskell, check.
It’s also time for a little call to action: don’t conflate the unit/acceptance/system testing hierarchy with the xUnit framework/boilerplate. There’s xUnit testing and then there’s fully randomized input generation ala QuickCheck, but there’s still room in-between these two distinct places in abstraction for people and tests to live. And of course, the xUnit style test can be useful when a code listing truly is the right paradigm for the input representation.
April 23, 2010The bag of programming tricks that has served us so well for the last 50 years is the wrong way to think going forward and must be thrown out.
Last week, Guy Steele came in and did a guest lecture “The Future is Parallel: What’s a Programmer to Do?” for my advanced symbolic class (6.945). It’s a really excellent talk; such an excellent talk that I had seen the slides for prior to the talk. However hearing Guy Steele talk about it in person really helped set things in context for me.
One of the central points of the talk is the call for more creative catamorphisms. Well, what is a creative catamorphism? To answer this question, we first have to understand what a catamorphism is. The functional programming crowd is well familiar with a few relatively banal examples of the catamorphism, namely the left fold and the right fold. One way to think about folds is simply a “level of abstraction” above a loop one might write in an imperative language. Another way to think of the fold is replacing the type constructor for the list (the cons or : operation) with another function, as seen in Cale Gibbard’s excellent diagrams:

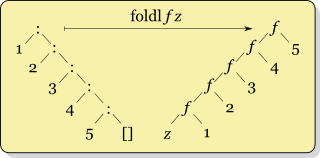
The point of the catamorphism is that this doesn’t need to apply just to lists; in fact, we can run a catamorphism on any recursive data structure! Just make a function for each constructor in the type, with the appropriate arity (so a ternary tree would require functions that take three arguments, and so forth), and let her rip! This is vitally important because the old left and right fold are the “wrong way to think”; by the very nature of their structure they require you to evaluate sequentially. But set things up in a binary tree, and you can evaluate all the subtrees first before combining them at the end.
So what is a creative catamorphism? It’s when the original recursive data structure doesn’t map cleanly on to the atoms that your computation wants to deal with. The example Guy Steele discusses in his talk is the time honored task of breaking a string into its words. A string is merely a list of characters, which only lets us handle it character by character (traditional sequential), or a naive transformation into a binary tree, which only gives us efficient bisection (parallelizable). The trouble with naive bisection is that it might split in the middle of the word, so our combining function has to account for this case. How to deal with this is left as an exercise for the reader (or you can go read the slides.)
In fact, this was the critical moment when I understood the global reasoning behind what Edward Kmett was talking about when he gave his (in my opinion pretty crazy) talk on “A Parallel Parsing Trifecta: Iteratees, Parsec, and Monoids”. The goal of this code is to massively parallelize parsing by splitting up the input document into chunks and then recombining them with the parsing function. He has to deal with the same problems that showed up in the toy example in Steele’s talk, and he pulls out all sorts of tricks to get things pumping.
I will admit, the work is complicated, and at times, it feels like overkill. But it’s a brave new parallel world, and it’s time we fully explore the designs and implications of it. With any luck, we will be able to write parallel programs as naturally we can write sequential programs, but it’s a long way getting there.
Update (2013-05-21). Oleg writes in to tell me that there is actually a name for these types of tricks: an almost homomorphism. It is not surprising to see that the work described in the Skepara project collaborated with Guy Steele and the Fortress project; it is well worth checking out for a calculational approach for deriving these catamorphisms.
April 21, 2010I recently some did some benchmarking of persistent data structures in mit-scheme for my UROP. There were a few questions we were interested in:
- For what association sizes does a fancier data structure beat out your plain old association list?
- What is the price of persistence? That is, how many times slower are persistent data structures as compared to your plain old hash table?
- What is the best persistent data structure?
These are by no means authoritative results; I still need to carefully comb through the harness and code for correctness. But they already have some interesting implications, so I thought I’d share. The implementations tested are:
All implementations use eq? for key comparison.

Unsurprisingly, assoc beats out everyone else, since all it has to do is a simple cons. However, there are some strange spikes at regular intervals, which I am not sure of the origin; it might be the garbage collector kicking in.

Of course, you pay back the cheap updates in assoc with a linear lookup time; the story also holds true for weight-balanced trees, which have fast inserts but the slowest lookups.

The hamt really flies when the key isn’t present, even beating out hash-tables until 15 elements or so.
Source code for running the benchmarks, our home-grown implementations, and graphing can be found at the scheme-hamt repository.
April 19, 2010In today’s world of social news aggregation websites, ala Reddit, Digg, Slashdot, it is rare for the sole dialog between an author and a reader to take place on a private channel or on one’s website. I discovered this rather bluntly when I found that a document I had written had amassed a number of comments, one of which pointed out an error in what I had written, and then failed to notify me.
These days, there is a certain amount of savvy that needs to be exercised in order to keep track of references on the Internet. Google Alerts, Twitter search, pingbacks… the list goes on and on. If you want to engage in a conversation with someone on the Internet, you’ll probably have to go to the medium they responded on, abide by the social conventions of that site and also risk being totally ignored (although that’s not as bad, since “you got the last word.”) If you’re a small company working carefully to cultivate good public relations around your product, you may even go as far to track down someone’s online identity and send them an email asking them if there’s any way you can help (it has been described as “creepily awesome customer service.”)
Then there’s also the flip side of the coin: to engage in a dialog with your reader, they need to know when you’ve responded! If they commented on their favorite social news site, they’ll get an update stream aggregating all of the other discussions they may be participating in. If they commented on the blog itself, options are far more varied: some blogs (like mine) offer no mechanism of notification when replies have been posted; others may offer “email notifications of replies” but fail to distinguish threads of conversation; some even outsource their discussion to a third-party provider like Disqus.
There are, of course, some who have lost faith in statesmanship over the Internet. Those are the people who you’ll see post essays with only a private email link for one-to-one conversation; those are the people who force their readers to unsponsored discussion on their favorite social media website; those are the people who shake their heads when the an ignorant commenter fails to display any indication that they read the article or know what they are talking about. I think that we can do better, because I’ve seen better! (Wink.) I’ve seen people comment, not because they want to project an image of smugness or superior knowledge, but because there is an earnest dialogue going on between all parties which, most of all, is focused on the transfer of knowledge. I’ve seen it happen on the Internet; I’ve seen it happen in real life; I still fall victim to the impulse to posture and chest-beat. I prefer conversing to people when the goal is to communicate, and not to win an argument. I enjoy arguing with people when I feel there is as much listening happening as there is talking. I love having an audience that consists of people, not an anonymous Internet.
April 16, 2010Conductor and violinist Gustavo Dudamel will be visiting MIT today to accept the Eugene McDermott Award in the Arts. Part of the awards ceremony will include a session with Dudamel conducting the MIT Symphony Orchestra; I’ll be on stage playing Oboe and English Horn on Rimsky Korsakov and Mozart. Our regular conductor (Adam Boyles) has been prepping us for this by taking, erm, unusual liberties in tempo and phrasing.
I’m not usually very aware of names of conductors, but I have heard Dudamel’s float across WQXR on occasion. The evening promises to be exciting.
Non sequitur. You can join PDF files together using pdftk input1.pdf input2.pdf input3.pdf cat output output.pdf. You can also use GhostScript, but this results in quality degradation since the file gets converted to PostScript first. (This may also explain why we keep finding 2.5GB PostScript files filling up our server disks.)
April 14, 2010data-accessor is a package that makes records not suck. Instead of this code:
newRecord = record {field = newVal}
You can write this:
newRecord = field ^= newVal
$ record
In particular, (field ^= newVal) is now a value, not a bit of extra syntax, that you can treat as a first-class citizen.
I came across this module while attempting to use Chart (of criterion fame) to graph some data. I didn’t recognize it at first, though; it was only after playing around with code samples did I realize that ^= was not a combinator that Chart had invented for its own use (as opposed to the potpourri of -->, <+>, ||| and friends you might see in an xmonad.hs). When utilized with Template Haskell, Data.Accessor represents something of a replacement for the normal record system, and so it’s useful to know when a module speaks this other language. Signs that you’re in a module using Data.Accessor:
- Use of the
^= operator in code samples - All of the records have underscores suffixed, such as
plot_lines_title_ - Template Haskell gobbledygook (including type variables that look like
x[acGI], especially in the “real” accessors that Template Haskell generated). - Unqualified
T data types floating around. (As Brent Yorgey tells me, this is a Henning-ism in which he will define a type T or typeclass C intended to be used only with a qualified import, but Haddock throws away this information. You can use :t in GHC to get back this information if you’re not sure.)
Once you’ve identified that a module is indeed using Data.Accessor, you’ve won most of the battle. Here is a whirlwind tutorial on how to use records that use data-accessor.
Interpreting types. An accessor (represented by the type Data.Accessor.T r a) is defined to be a getter (r -> a) and setter (a -> r -> r). r is the type of the record, and a is the type of the value that can be retrieved or set. If Template Haskell was used to generate the definitions, polymorphic types inside of a and r will frequently be universally quantified with type variables that x[acGI], don’t worry too much about them; you can pretend they’re normal type variables. For the curious, these are generated by the quotation monad in Template Haskell).
Accessing record fields. The old way:
fieldValue = fieldName record
You can do things several ways with Data.Accessor:
fieldValue = getVal fieldname record
fieldValue = record ^. fieldname
Setting record fields. The old way:
newRecord = record {fieldName = newValue}
The new ways:
newRecord = setVal fieldName newValue record
newRecord = fieldName ^= newValue $ record
Accessing and setting sub-record fields. The old ways:
innerValue = innerField (outerField record)
newRecord = record {
outerField = (outerField record) {
innerField = newValue
}
}
The new ways (this is bit reminiscent of semantic editor combinators):
innerValue = getVal (outerField .> innerField) record
newRecord = setVal (outerField .> innerField) newValue record
There are also functions for modifying records inside the state monad, but I’ll leave those explanations for the Haddock documentation. Now go forth and, erm, access your data in style!




