ezyang's blog

Quote Day

Unattributed to protect the innocent. (But you can probably guess.)

“And so these poor programmers, they had to drink this much whiskey to get the job done.” [triumphantly produces a bottle of whiskey and places it on the table.] “And this group of programmers did X, and how hard was that? Two bottles of whiskey.” [places two more bottles of whiskey on the table] “But that wasn’t fast enough. And so this group of programmers did Y. Four bottles of whiskey.” [four more bottles appear] “As you can see, this is requiring an exponentially increasing amount of whiskey.”

“Locks and semaphores are Soviet-era technology.”

On the subject of optimizing algorithms by porting them to lower level hardware description languages: “There are much more productive things for you young PhD students to be doing.”

On Tycho Brahe: “Drunk. Irascible. Fat. Brilliant. Definitely a role model.”

“One of the benefits of Hindley-Milner inference is that it’s quite efficient.” “You mean EXPTIME-complete.”

“Any god-fearing man should write his type signatures.”

On the absence of let generalization in GHC 7.0: “It’s not a feature, it’s a bug with benefits.”

“You would think that explicit type signatures would make the type checker’s job easier, but actually they are making the checker’s job harder.”

“I strongly recommend this paper, but do carry along a jar of aspirin.”

Why being a sysadmin will help you do Science!

A complaint I once heard about SIPB is that it leans too much towards the system administration side: we proudly display the services we have deployed and neglect to talk very much about actually programming or conducting novel computer science research (despite the fact that we are very much programmers and some of us are quite research oriented.) So if you’re really not at all interested in that sort of thing (like me) you might think to yourself, “That’s very nice” and go and do something else.

I think this is a mistake, and that even a short period of time administrating a system larger than your personal laptop can be tremendously helpful for any work with computers you may do, whether it’s software engineering or computer science. System administration is advanced computer literacy, it’s a bit like knowing how to operate a complicated telescope. Sure, it has nothing to do with actually studying the stars or the fundamental nature of computation, but you’ll sure get a lot more done if you’re not fumbling with your equipment. System administration is what we do to get other things done.

“Sure,” you may say, “but any practicing software engineer or computer scientist will pick up the bits and pieces of system administration they need to know.” Yes, but I will argue that unless you actively seek out sysadmin tasks, the set of skills you acquire will be the bare minimum to get what you need done. Much like strength training, you are only actively gaining sysadmin skills when you’ve been pushed beyond what you’re ordinarily capable of. But unlike strength training, the benefits don’t go away after you’re done: you keep using the tricks you learned for everyday tasks. And what better way to push yourself further than to administrate a system for others?

To which I say, SIPB is a fantastic opportunity for this sort of work. It’s rare to be able to work on systems of this size and scope as an undergraduate: class projects don’t even come close. And if you’re a graduate student, you may be building complex systems but you may also be the only one using them, and having users is an enlightening experience (despite the fact that we sometimes complain, “Can we deprecate users?”)

Here are some personal perks that I’ve picked up from SIPB:

• I now know how to RAID two disks together, forced to learn how to do so because of standard operating procedure in our project. It’s not something that I would have gone out and done before, but now I consider it essential to any new physical server I setup. Because, for disk failure, it’s not a question of if, it’s a question of when.
• I now know how to effectively source dive code. I’ve used this to help communicate more effectively with upstream, fix bugs, add features, fill in for missing documentation, and more.
• I understand how the MIT Athena infrastructure works at a much more fundamental level.

The HTML purification manifesto

I recently sent Greg Weber an email about his xss-sanitize package, cautioning about his reuse of the pandoc sanitization algorithm for his own package. He responded (with good justification) that a mere caution was not very constructive! So here is my response, the “HTML purification manifesto,” which HTML Purifier follows and which I think is a prerequisite for any industrial grade HTML sanitization library. I will admit it’s a tough manifesto to follow, and I’ll talk about when you can get away with not following it to the line.

The manifesto.

Use semantic data structures. Many filters attempt to never build up a DOM or tokenized representation of their HTML during the processing stage for performance reasons. It turns out this makes securing your filter notoriously difficult. Consider the XSS cheatsheet: see how many of the vulnerabilities involve non-well-formed HTML. If you require HTML to be converted into a DOM, and then serialize it out again, you have a pretty good guarantee that the result will be well-formed, and you eliminate all of those vulnerabilities.

This must be applied to all sublanguages in HTML, and not just HTML itself. You also have to be careful that your serializer produces standards compliant output. For example, a vulnerability in HTML Purifier itself was caused by a lax adherence to standards. As it states:

HTML Purifier’s fix also percent-encodes any other reserved character in each segment of a URI. This was actually a previously identified section of relaxed standards compliance, and strictly enforcing the rules eliminated the vulnerability.

Semantic data structures are also useful for implementing extra features—for example extracting content from the document or converting all URIs into absolute form—and makes validation and manipulation tremendously easier. It will also be critical for the next step.

Whitelist and validate everything. Whitelisting is a well accepted practice, and I will not harp on it here. However, there are subtleties in its application. In order to understand the first part of the manifesto, you need to understand what everything means. At first glance, the obvious things that you might have to whitelist are elements and attributes. But if you decide to allow the href attribute, you need to make sure you whitelist URI schemes too—three things to whitelist. And heaven forbid you decide to allow style attributes!

It’s far better to take a different approach to whitelisting: every time you encounter an attribute, figure out what its sensible values are, and validate it to a whitelist. Think you don’t need to validate that height? Consider the imagecrash attack, which can bluescreen an unwitting Windows user simply by setting the width and height of an image to 999999. Complicated attribute? It may have further structure, so expand it into the appropriate semantic data structure! (The most obvious candidates are URIs and CSS strings.) You don’t necessarily have to create these structures in memory (indeed, an optimized implementation would try to avoid it), but it certainly makes coding the algorithms a lot easier. Also, it is much easier to manipulate the resulting semantic structure than it is to manipulate a bunch of strings.

This is a rather large problem to tackle, because there are so many elements and attributes in HTML and so many sublanguages embedded within those. However, you can dramatically simplify matters by creating a domain specific language to help you declaratively specify what the semantics are: though I didn’t know it at the time, this was the approach that HTML Purifier took with its HTMLModule system.

Output only what all browsers understand. I used to believe that standards compliance was enough to make sure all browsers understood your syntax (the primary target of most exploits.) Sometimes, however, browsers just don’t parse by the standards at all. Usually, the wild and woolly fields of ambiguous behavior lie outside the dictates of standards, but sometimes the standard says X should happen and Internet Explorer goes and does Y. It is tempting to throw your hands up in the air and just deal with the vulnerabilities as they come in.

But because this is an incompatibility with the standards, there are many web developers have discovered that what should work doesn’t! For CSS, even the most obscure parsing bug in Internet Explorer has been tripped over by some web developer and been documented in a wiki or encoded into a CSS hack. This knowledge, while seemingly not related to the questions of security, is critical for someone writing an HTML filter! It tells you, in particular, what the subset of standards-compliant HTML that is understood by all browsers is.

A more practical note. Whenever I see a new HTML filter pop up on the web, I apply these three litmus tests to the source code (I don’t even bother trying the demo):

1. Does it use an HTML parser or attempt to do a bunch of string transformations?
2. How much does it whitelist? Just elements and attributes? What contents of attributes does it treat?
3. Does the filter appear to have accreted those battle scars that come from dealing with the real world?

I apply the second and third criterion less strongly depending on what the filter claims to support: for example, a filter with no support for CSS needs not worry about its attendant difficulties. In the extreme case, if you’re writing a filter for just <b> and <i>, you can get away with not following any of these recommendations and be fine. But I suspect users always want more features, and you will inevitably start adding new elements and attributes. So I also judge whether or not the source seems to have thought about extending itself in these directions.

A more linguistic note. I use the word “purification” rather than “sanitization”, because sanitization implies that the pathogens have merely been rendered inert, whereas purification implies that they have actually been removed altogether. I think that the latter philosophy is a much safer stance!

Conclusion. Back in the day, I managed to write highly inflammatory comments about other HTML filters in an overzealous attempt to promote my own. I avoid doing direct comparisons these days; instead, I hope this manifesto is helpful to people interested in writing or improving their own filters.

Abstraction without a concrete concept

Hoare logic, despite its mathematical sounding name, is actually a quite practical way of reasoning about programs that most software engineers subconsciously employ in the form of preconditions and postconditions. It explicitly axiomatizes things that are common sense to a programmer: for example, a NOP should not change any conditions, or if a line of code has a postcondition that another line of code has as its precondition, those lines of code can be executed one after another and the inner precondition-postcondition pair ignored. Even if you never actually write out the derivation chains, you’re informally applying Hoare logic when you are trying to review code that uses preconditions and postconditions. Hoare logic is an abstraction that lets us rigorously talk about any imperative language with the same set of rules.

At my very first Semantics lunch, I was treated to a talk by Tony Hoare entitled Abstract Separation Algebra. Unhappy with the fact that the separation logic requires you to talk about three things: the precondition, the actual code, and the postcondition, Tony Hoare re-encoded the scheme as vanilla abstract algebraic structures. While his slides all seemed plausible my abstract algebra wasn’t facile enough to be able to verify all of his results as they flashed by. Accordingly, I’m not going to talk too much about the actual reencoding (I need to work it out myself when I get some free time, ha!). However, I caught a whiff of the underlying thought process that was driving this reencoding, which I thought was a fascinating way of thinking: take an axiom X of your abstraction that you would like to be true, and with a more fundamental pool of axioms (in this case, the usual axioms of abstract algebra) figure out which ones are necessary to make axiom X logically true. This is mind twisting in several ways, not the least of which is that you end up with a set of primitives for which you may not even have a concrete model for!

I will admit, I am a little afraid that the mathematicians in the audience will think, “Well, of course that’s how you pick your set of axioms! And pff, concrete models are for the weak.” (After all, it was said in the talk, “This is abstract algebra, so you should be willing to accept these axioms without having any model in mind.”) But given the questions asked during the talk, among them “so what intuitively does ★ mean?” (for which there was no answer) I think I am justified in claiming that for some of us mortals, this is a rather strange way of thinking about things.

For example, consider the first example that Hoare gave: let (C, ;, ⊑) be a ordered semigroup (that is, a carrier set C equipped an associative binary operation ; that is monotonic with respect to a partial ordering relation ⊑.) Then, we can define the Hoare triple {p} q {r} as the relation p ; q ⊑ r. I immediately want to know: what does C represent (it appears to contain postconditions, lines of code, and preconditions: as Simon Peyton Jones pointed out, it doesn’t seem to distinguish these two types of code) and what does the relation ⊑ represent? But these are rather unimportant questions, since if we shake this algebra-tree, the fruit of sequential composition drops down by monotonicity:

Alas, the humble ordered group isn’t enough to encode all of the things we need, so Hoare ends up bringing monoidal lattices and special operators that obey the abides law in order to get the “Separation Algebra”:

As he admits, he is cheating slightly: he is bringing in precisely the algebraic properties he needs in order to get the properties he wants. But what makes the result notable is the fact that all he needed were the well-studied structures of vanilla abstract algebra. Consequently, when we manipulate our newly encoded Hoare triples, we can rely on the good old techniques of abstract algebra (which, for those of us who never took abstract algebra, may not be “good” or “old.”)

So what do ⊑, ★, ε and ⊔ mean? Because of how we’ve constructed our algebraic structure, we don’t necessarily know! (Although, I’m sure some concrete model is out there just waiting to be discovered. Maybe it’s been discovered already.) Perhaps this is all just an illustration of the category theory mantra: “The self is unimportant: only its relation to others.” A bit zen, if you ask me.

Postscript. There was a nice comment about how the duality between the implementation and specification algebras resembled the Stern dualities: very roughly, that two points determine a line, but a line determines an infinite number of points. I went and searched for the term but couldn’t find any literature about this, so perhaps some pointers would be appreciated.

Why I am in Cambridge

I am studying computer science this academic year at Cambridge University, not MIT. For some people, this seems quite strange: when I tell old friends at MIT and new acquaintances at Cambridge about the fact that I am a Cambridge-MIT Exchange student, they say, “Why?” Sometimes, it’s some disbelief at the fact that I am choosing to leave the familiar social circles and situations that mark MIT. Other times, it’s some disbelief that I would want to study computer science at Cambridge rather than MIT (“Just joking,” they add, though I’m not necessarily sure I believe them.)

I would like to explain why, in terms of both before leaving for Cambridge and also how my perspectives have changed after a mere three days in the college. This is a post for future students considering CME, my parents who anxiously want to know how I am doing at Cambridge, and for everyone who may at some point have asked me why. Oh, and there might be something about the functional programming research in Cambridge. wink

Foreign exchange program was always something I had vague intentions of doing while applying to colleges. When you haven’t done sufficient thinking about a subject, or haven’t experienced enough to really have enough data, your ideas are molded by platitudes and truisms like “it will be a good experience” and “you’ll learn more about the world than just the US.” It’s a bit like describing a hurricane as ‘wet’; it’s vacuously true and not very useful. My impressions about what college life might be like were similarly vague.

MIT swept away those preconceptions and made me understand what my college life would be like. And, to tell the truth, I liked it. MIT is busy—it doesn’t give much time for introspection—but when I was able to step away from it all for just a moment and see myself talking about how chroots work while walking home from the Stata center, or working out with a person I really respect and admire how to encode the Futamura projections in Haskell, or finding myself in control of a fictional economy in a live-action role playing game, or staying up all night in a room with my friends talking about relationships until the sun pokes through the window… it makes you fiercely loyal to the place. By the end of my freshman year summer, I was incredibly ready to return to MIT.

But MIT is a slightly pathological environment (perhaps that’s how it attracts the people it does.) And one of the things it is able to do is make you tired. Not just from missing sleep: it also stems from things like having been up for classes since 10AM and having had not more than hour to yourself before some other class or activity demanded your time. Though I have never definitively burned out (usually a weekend of marathoning some TV show is enough to cure me), I see many of my friends constantly sparring with (and occasionally succumbing to) the beast. But I found myself feeling tired, and when the information session for the CME program came up, it seemed extremely timely.

I was not really alone in feeling this way; I saw some familiar faces at the information session, and they expressed similar feelings. And some of these people, in the end, decided not to do the program, because they just couldn’t bring themselves to leave MIT. I suspect that just “feeling tired” would not have been enough to make me go to Cambridge. But the topic had brought back a memory of the summer of my Junior year that became a driving force.

This was the possibility of an alternate reality Edward; one who had not gone to a university where computer scientists were not spilling out of the walls and my social groups were not almost entirely composed of people who, in some way or another, were studying science or engineering. A universe where Edward had gone to a liberal arts university where people did not constantly boast about how “hosed” they were. Post-MIT, it would have been impossible to imagine, except for the fact that I had attended a little program called Governor’s School for the Arts and put away my computer for my oboe and hanged out in the room of a creative writer with artists, actors and other musicians. It was just a month: a mere taste. But it was a taste I never forgot.

It was enough to make me seriously consider the possibility, and let my parents know about it. They strongly approved, which pushed me even further. I decided I’d write the requisite essay and see if they’d admit me. They did.

There are not many major decisions in my life that I have agonized over. This one was a whisper in the cacophony of MIT life. I accepted, and it was a simple, plain fact, with no real impact on my life. MIT was still MIT, my life was still ordinary, life moved on.

My father had always bugged me to “have lunch with every computer science professor at MIT.” I went as far to compile a list of all of the professors and their rooms, so that I could track them down in person. But I never did it: I could never figure out what we would talk about, and in that case, it seemed like a waste of both my time and the professor’s time, unless he was feeling in the mood for doing a bit of advocacy for his work.

Summer at Galois set my decision that I wanted to pursue functional programming in some shape or form as a computer scientist. Once I figured out what it was I actually doing, it was as if my eyes were opened. I learned about research groups at MIT that I had never heard about before, I suddenly discovered that I had a small kernel of research ideas that I could grow as I read and learned more about the computer science research. I had not thought at all about the academics of Cambridge (such a famous university ought to have a sufficient computer science department.)

Now I looked, and I was quite pleased to discover that Cambridge University seemed to be more in line with these research interests than MIT was. The basic undergraduate curriculum covers such topics as denotational semantics, types and Hoare logic. Simon Peyton Jones and Simon Marlow, my two idols, work at Microsoft Research Cambridge. It’s right next to the Cambridge Computer Lab: I dropped by just to squee at the location before heading back home. Several research groups work in areas that feed into functional programming: the Automated Reasoning group holds lunches with talks every week. Glasgow, which was the epicenter of the functional programming movement a few decades ago, is within striking distance.

I believe in the ability for individuals to shape their destiny, but I don’t really believe people know what they’re shaping it to: they just make adjustments when things happen that they don’t like. And sometimes it takes a giant irrational change to move you out of the local optimum. My reasons for going to Cambridge are irrational: how do I know if Cambridge will be less stressful than MIT or if I will actually restore parts of that alternate universe Edward. It’s entirely up to me whether or not I take advantage of the resources around me in Cambridge (I haven’t yet, but it’s only four days in…) But here I am. Nothing has happened yet. But everything is in place. And I am optimistic.

Tips for running a hackathon

A hackathon is an event, spanning from a day to a week, where hackers (not the cracking kind) get together to work on some common goals in concert. One use of a hackathon is to get some open-source contributors together and work hard on a particular feature: the combination of being together and being expected to work on the task at hand means that people are more productive than they would be if they were just working alone.

However, at SIPB, we use hackathons in a different way: in fact, this type of a hackathon could be said to make maintainers less effective at whatever tasks they may have on hand. The idea of this hackathon is to get new people interested and working on existing projects. This is vital in a university environment, where people graduate after only four years and we constantly need to be looking for fresh people.

Here are some off-the-cuff tips that I’ve noticed help make these sorts of hackathons more successful when the day rolls around.

• Communicate to established project members that you will not get stuff done until the wee hours of the hackathons, when the prospectives have left. Expect to be answering questions, helping people get set up, and generally being attentive to the activity around the hackathon on your project.
• Establish a list of tasks to work on before the hackathon begins. Parallelization is hard, even in the real world, and so you should already have bite-sized independent pieces of work to give to prospectives who are ready to just start working.
• Have a lot of tasks. People have different interests, even though they will undoubtedly tell you, “Oh, anything is ok,” and you should make it clear that if they’re not having fun working towards some task, maybe they could try a different one.
• Have tasks of differing difficulty. Yes, it’s nice when that one person walks in, has the development environment setup in half an hour, and manages to finish his task way before the end of the hackathon. Most people are not like that; for some, setting up a development environment is a task that can consume an entire afternoon and evening. This is frustrating. Let them know that there are things that they can actually make productive progress on.
• Keep track of who’s working on what and the final achievements. It’s really nice to be able to say what was accomplished at the end of the hackathon; it makes people feel good and encourages them to come back.
• Check in with prospectives, but not too often. It’s good to check half an hour after getting someone started how they are doing and help them out if they’re struggling. But check on them too much and you can easily make them feel nervous or pressured, which is not fun and therefore not OK for a hackathon.
• Take advantage of questions that require “long answers.” If someone suggests X and in fact, we’ve thought about it but can’t do X for some complicated reason Y, don’t wave the question off: tell the person about Y. They might even have a reason around it, and either way, they learn more about the system they are working on in a really effective way: knowledge as you need it.
• Be an enabler. Do the boring, tedious tasks that you’ve procrastinated on if it would make a prospective more effective and have more fun on a task. You can trick them into doing those “housekeeping” tasks later, when they’re invested in the project. (wink)

I encourage past hackathon organizers to also share their wisdom!

How to get answers from busy maintainers

As one of those “busy maintainers,” I’ve noticed that I assume a certain cognitive mode when fielding support requests. This post is about how I deal with support requests, but I’ve also seen this behavior widely on other projects. While, as the person making the request, you may find such a mentality frustrating and obtuse, if you are a fellow developer you can use it in your favor.

What do I think when I see your support request?

• I want to help you. If I wasn’t interesting in answering your questions, I would have desupported this project. However…
• I want to fix the issue with as little cognitive effort as possible. I want to use my brain power thinking about new features and theory, not doing sleuthing for the user. Relatedly,
• I want to fix the issue with as little real effort as possible. If I have actually do things to figure out how to fix your problem, I’m more inclined to procrastinate on it. Add a doubling modifier if I’m not sure what I need to do. Paradoxically, if I have access to your setup, I might just go and fix it, because my usual debugging cycle is much faster than, “Ask you to try something or get some information and report it to me.”

Notice that feature requests operate on a different set of rules. For scratch an itch software I may have little interest in features that don’t help me. But if I am going to put a feature in that doesn’t immediately help you, I want to do it right—just because it works for you doesn’t mean it should be in my codebase. And, of course, the moment it’s someone else trying to get code in, my code standards shoot way up.

In accordance with these principals of benevolent laziness, answers to support requests you get might be:

• Short,
• A guess that it’s some common issue that you may have already noticed while Googling (you did try Googling it first, right?),
• Asking you for more (sometimes seemingly irrelevant) information,
• Asking you to try something that may or may not work, and
• Late. (I set aside some time every few weeks to go through their open tickets, and you won’t get an answer until then.)

So how do you use these facts to your favor?

• Don’t assume that your problem is the same as someone else’s. Support requests are not bugs! They may be generated by bugs, but every support request has its own individual flavor to it, and until its cause is pinned down to a specific technical issue, you’re muddying the waters if you decide that your problem is the same as some other complicated problem. Reference the existing bug or support request in your request and let the maintainer decide.

• Give me lots of information, even if you think it’s unnecessary. Why did you make this support request? I can’t speak for everyone, but when I ask for help it’s usually because I believe that someone out there has a much more comprehensive big picture and because I believe that they will have some insight that I don’t have. So why do I have any reason to believe some debugging information that I think is useless won’t help someone who is much more attuned to the software divine the problem? Furthermore, if I am only looking at support requests once every two weeks, you better hope you’ve given me enough information to figure it out when I actually look at your request.

  Relatedly, don’t be tempted to “curate” the information: some of the worst debugging sessions I’ve had were because I misinterpreted some evidence I got, and then acted on that wrong assumption.

• Make it easy for the maintainer to debug the problem. Minimal test cases, minimal test cases, minimal test cases. It’s even better if it’s running code that doesn’t require any setting up, but frequently the specific setup will have the information the maintainer needs to figure out your problem.

• Do your own debugging. You’ve handed the maintainer a problem that they don’t know an answer off the top of their head to. It might be a real bug. If they’re particularly accommodating, they’ll try to recreate your problem and then debug it from their local setup; if they’re not, they’ll try simulating their debugging process through you. You can tell that this is the case when the start asking you for specific pieces of information or tweaks. Don’t let them initiate this lengthy and time-consuming process: do your own debugging. Because you are seeing the problem, you are the best person to actually debug it.

  “But,” you might say, “Why should I voluntarily debug other people’s code!” This case is a little different: this is not legacy code where the original author is nowhere to be found: you have a benevolent upstream willing to help you out. You have someone to sanity check your results, tell you what tools to use (something like PHP will be easy to debug: just edit some source files; something like a C application is tougher, but gdb with debug symbols can work wonders), point you in the right direction and short-circuit the rest of the process when you tell them some key piece of information. The key bit is: if you have a question about the software, and you know an experiment you can run to answer that question, don’t ask: run the experiment.

• Make me fix my documentation. I’m worried about answering your question, not necessarily about fixing my software. If there is some doc somewhere that was unclear, or some runtime check that could have prevented you from needing to ask your question, make me fix it by pointing it out! Different people absorb information differently, so it’s good if as many ways as possible to communicate some piece of information are available.

So long America!

For tomorrow I get on a plane traversing three thousand miles from my home to a little place named Cambridge, United Kingdom. I’ll be studying abroad for the 2010-2011 academic year at Cambridge University (specifically, I’ll be at Fitzwilliam college). While I know Baltimore is a fashionable place to be these days, if you’re in the area, drop me a line: I’d love to meet up after I get over my jet lag. :-)

High performance monads

Continuations are well known for being notoriously tricky to use: they are the “gotos” of the functional programming world. They can make a mess or do amazing things (after all, what are exceptions but a well structured nonlocal goto). This post is intended for readers with a passing familiarity with continuations but a disbelief that they could be useful for their day-to-day programming tasks: I’d like to show how continuations let us define high performance monads ala the Logic monad in a fairly methodical way. A (possibly) related post is The Mother of all Monads. :

> import Prelude hiding (Maybe(..), maybe)

We’ll start off with a warmup: the identity monad. :

> data Id a = Id a
> instance Monad Id where
>     Id x >>= f = f x
>     return = Id

The continuation-passing style (CPS) version of this monad is your stock Cont monad, but without callCC defined. :

> data IdCPS r a = IdCPS { runIdCPS :: (a -> r) -> r }
> instance Monad (IdCPS r) where
>     IdCPS c >>= f =
>         IdCPS (\k -> c (\a -> runIdCPS (f a) k))
>     return x = IdCPS (\k -> k x)

While explaining CPS is out of the scope of this post, I’d like to point out a few idioms in this translation that we’ll be reusing for some of the more advanced monads.

1. In order to “extract” the value of c, we pass it a lambda (\a -> ...), where a is the result of the c computation.
2. There is only one success continuation k :: a -> r, which is always eventually used. In the case of bind, it’s passed to runIdCPS, in the case of return, it’s directly invoked. In later monads, we’ll have more continuations floating around.

Following in step with monad tutorials, the next step is to look at the venerable Maybe data type, and its associated monad instance. :

> data Maybe a = Nothing | Just a
> instance Monad Maybe where
>     Just x >>= f = f x
>     Nothing  >>= f = Nothing
>     return = Just

When implementing the CPS version of this monad, we’ll need two continuations: a success continuation (sk) and a failure continuation (fk). :

> newtype MaybeCPS r a = MaybeCPS { runMaybeCPS :: (a -> r) -> r -> r }
> instance Monad (MaybeCPS r) where
>     MaybeCPS c >>= f =
>         MaybeCPS (\sk fk -> c (\a -> runMaybeCPS (f a) sk fk) fk)
>     return x = MaybeCPS (\sk fk -> sk x)

Compare this monad with IdCPS: you should notice that it’s quite similar. In fact, if we eliminated all mention of fk from the code, it would be identical! Our monad instance heartily endorses success. But if we add the following function, things change:

> nothingCPS = MaybeCPS (\_ fk -> fk)

This function ignores the success continuation and invokes the failure continuation: you should convince yourself that one it invokes the failure continuation, it immediately bugs out of the MaybeCPS computation. (Hint: look at any case we run a MaybeCPS continuation: what do we pass in for the failure continuation? What do we pass in for the success continuation?)

For good measure, we could also define:

> justCPS x = MaybeCPS (\sk _ -> sk x)

Which is actually just return in disguise.

You might also notice that the signature of our MaybeCPS newtype strongly resembles the signature of the maybe “destructor” function—thus called because it destroys the data structure:

> maybe :: Maybe a -> (a -> r) -> r -> r
> maybe m sk fk =
>     case m of
>         Just a  -> sk a
>         Nothing -> fk

(The types have been reordered for pedagogical purposes.) I’ve deliberately named the “default value” fk: they are the same thing! :

> monadicAddition mx my = do
>   x <- mx
>   y <- my
>   return (x + y)
> maybeTest    = maybe       (monadicAddition (Just 2)   Nothing)    print (return ())
> maybeCPSTest = runMaybeCPS (monadicAddition (return 2) nothingCPS) print (return ())

Both of these pieces of code have the same end result. However, maybeTest constructs a Maybe data structure inside the monadic portion, before tearing it down again. runMaybeCPS skips this process entirely: this is where the CPS transformation derives its performance benefit: there’s no building up and breaking down of data structures.

Now, to be fair to the original Maybe monad, in many cases GHC will do this transformation for you. Because algebraic data types encourage the creation of lots of little data structures, GHC will try its best to figure out when a data structure is created and then immediately destructed, and optimize out that wasteful behavior. Onwards!

The list monad (also known as the “stream” monad) encodes nondeterminism. :

> data List a = Nil | Cons a (List a)
> instance Monad List where
>     Nil >>= _ = Nil
>     Cons x xs >>= f = append (f x) (xs >>= f)
>     return x = Cons x Nil
> append Nil ys = ys
> append (Cons x xs) ys = Cons x (append xs ys)

Nil is essentially equivalent to Nothing, so our friend the failure continuation comes back to the fray. We have to treat our success continuation a little differently though: while we could just pass it the value of the first Cons of the list, this wouldn’t let us ever get past the first item of the list. So we’ll need to pass our success continuation a resume continuation (rk) in case it wants to continue down its path. :

> newtype LogicCPS r a = LogicCPS { runLogicCPS :: (a -> r -> r) -> r -> r }
> instance Monad (LogicCPS r) where
>     LogicCPS c >>= f =
>         LogicCPS (\sk fk -> c (\a rk -> runLogicCPS (f a) sk rk) fk)
>     return x = LogicCPS (\sk fk -> sk x fk)

Remember that return generates singleton lists, so there’s nothing more to continue on to, and we give the success continuation fk as the resume continuation.

The old data constructors also can be CPS transformed: nilCPS looks just like nothingCPS. consCPS invokes the success continuation, and needs to generate a resume continuation, which conveniently enough is given by its second argument:

> nilCPS =
>     LogicCPS (\_ fk -> fk)
> consCPS x (LogicCPS c) =
>     LogicCPS (\sk fk -> sk x (c sk fk))
> appendCPS (LogicCPS cl) (LogicCPS cr) =
>     LogicCPS (\sk fk -> cl sk (cr sk fk))

These types should be looking awfully familiar. Rearranging this type a little (and renaming b→r):

foldr :: (a -> b -> b) -> b -> [a] -> b

I get:

fold :: List a -> (a -> r -> r) -> r -> r

Hey, that’s my continuation. So all we’ve done is a fold, just without actually constructing the list!

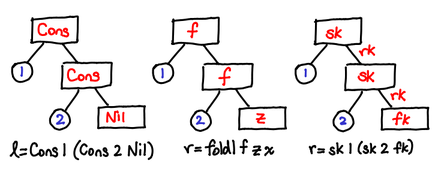
Keen readers will have also noticed that the CPS formulation of the list is merely the higher-order Church encoding of lists.

The CPS transformed version of the list monad wins big in several ways: we never need to construct and destruct the list and appending two lists takes O(1) time.

One last example: the leafy tree monad (cribbed from Edward Kmett’s finger tree slides):

> data Leafy a = Leaf a | Fork (Leafy a) (Leafy a)
> instance Monad Leafy where
>     Leaf a >>= f = f a
>     Fork l r >>= f = Fork (l >>= f) (r >>= f)
>     return a = Leaf a

As it turns out, if we want to fold over this data type, we can reuse LogicCPS:

> leafCPS x = return x
> forkCPS l r = appendCPS l r

To go in the other direction, if we combine all of the CPS operations on logic we’ve defined thus far and turn them back into a data type, we get a catenable list:

> data Catenable a = Append (Catenable a) (Catenable a) | List (List a)

To wrap (fold) up, we’ve shown that when we build up a large data structure that is only going to be destructed when we’re done, we’re better off fusing the two processes together and turn our data structure back into code. Similarly, if we would like to do “data structure”-like things to our data structure, it is probably better to actually build it up: the Church encodings for things like tail are notoriously inefficient. I’ve not said anything about monads that encode state of some sort: in many ways they’re a different breed of monad from the control flow monad (perhaps a more accurate statement is “Cont is the mother of all control flow monads”).

To quote Star Wars, the next time you find yourself entangled in a mess of continuations, use the data structure!

Addendum. CPS transforming data structure traversal has nothing to do with monads. You can do it to anything. It just so happens that the killer feature of control flow monads, nondeterminism, happens to really benefit from this transformation.

References. There are loads and loads of existing treatments of this subject.

• haskell.org wiki mentions CPS transforming monads for performance,
• This mailing list thread seems to imply that CPS transformation can make code slower, but in fact, they never ditch the construction of their data type.
• Representing variant types uniformly via executable code has a long and proud tradition under the term tagless. Some of them include Oleg’s treatment for embedded languages and the GHC developer’s Spineless Tagless G-machine under the hood.
• This ICFP presentation notes the similarity between the stream monad and the backtracking logic monad, and unifies the two with the moral equivalent of a fold.

I’ve probably missed a bunch of other obvious ones too.

Data is Code

Yesterday I had the pleasure of attending a colloquium given by Chung-Chieh Shan on Embedding Probabilistic Languages. A full account for the talk can be found in this paper, so I want to focus in on one specific big idea: the idea that data is code.

Lispers are well acquainted with the mantra, “code is data,” the notion that behind every source code listing there is a data structure of cons-cells and tags representing the code that can constructed, modified and evaluated. With this framework, a very small set of data is code: '(cons 1 (cons 2 ())) is code but '((.5 ((.5 #t) (.5 #f))) (.5 ((.5 #t)))) isn’t.

Under what circumstances could the latter be code? Consider the following question (a hopefully unambiguous phrasing of the Boy-Girl paradox):

You close your eyes. I hand you a red ball or a blue ball. Then, I will hand you a red ball or a blue ball. You then peek and discover that at least one of the balls is red. What are the odds that the first one was red?

Those of you familiar with probability might go write up the probability table and conclude the answer is 2/3, but for those who are less convinced, you might go write up some code to simulate the situation:

a <- dist [(.5, red), (.5, blue)]
b <- dist [(.5, red), (.5, blue)]
if a != red && b != red
  then fail
  else a == red

Where dist is some function that randomly picks a variable from a distribution, and fail reports a contradiction and ignores the generated universe. This code is data, but it is data in a much deeper way than just an abstract syntax tree. In particular, it encodes the tree of inference '((.5 ((.5 #t) (.5 #f))) (.5 ((.5 #t)))):

O               O    
/ \             / \   
/   \           /   \  
R     B        .5    .5 
/ \   / \       / \   / \
RR RB BR BB    .25.25.25  
           #t #t #f  

Aside. Interested Haskellers may now find it instructive to go off and write the naive and continuation passing implementations of the probability monad suggested by the above code, a monad which, when run, returns a list of the probabilities of all possible outcomes. It is an interesting technical detail, which will possibly be the subject of a future blog post, but it’s treated quite well in sections 2.2, 2.3 and 2.4 of the above linked paper and fairly standard practice in the continuation-using community.

Now, I haven’t really shown you how data is code; rather, I’ve shown how code can map onto an “abstract syntax tree” representation or an “inference tree” representation. However, unlike an AST, we shouldn’t naively build out the entire inference tree: inference trees whose nodes have many children can branch out exponentially, and we’d run out of memory before we could do what is called exact inference: attempt to build out the entire inference tree and look at every result.

However, if we follow the mantra that “data is code” and we represent our tree as a lazy data structure, where each child of a node is actually a continuation that says “build out this subtree for me,” we recover an efficient representation. These continuation can, themselves, contain more continuations, which are to be placed at the leaves of the subtree, to be applied with the value of the leaf. Thus our data structure is, for the most part, represented by code. (This is in fact how all lazy data structures work, but it’s particularly poignant in this case.)

Even more powerfully, first-class support for delimited continuations means that you can take a regular function () -> e and reify it into a (partial) tree structure, with more continuations as children ready to themselves be reified. We can, of course, evaluate this tree structure to turn it back into a function. (Monads in Haskell cheat a little bit in that, since lambdas are everywhere, you get this representation for free from the abstraction’s interface.)

What I find really fascinating is that a whole class of algorithms for efficient probabilistic inference become obvious when recast on top of an inference tree. For example:

• Variable and bucket elimination corresponds to memoizing continuations,
• Rejection sampling corresponds to randomly traversing paths down our tree, discarding samples that result in contradictions (fail), and
• Importance sampling corresponds to randomly traversing a path but switching to another branch if one branch fails.

Being a shallow embedding, we unfortunately can’t do things like compare if two continuations are equal or do complex code analysis. But some preliminary experimental results show that this approach is competitive with existing, custom built inference engines.

There’s a bigger story to be told here, one about DSL compilers, where we give users the tools to easily implement their own languages, thereby increasing their expressiveness and productivity, but also allow them to implement their own optimizations, thereby not trading away speed that usually is associated with just writing an interpreter for your language. We’d like to leverage the existing compiler framework but add enhancements for our own problem domain as appropriate. We’d like to give behavioral specifications for our problem domains and teach the compiler how to figure out the details. It’s not feasible to write a compiler that fits everyone, but everyone can have the compiler spirit in them—and I think that will have an exciting and liberating effect on software engineering.