March 7, 2011They say that one doesn’t discover advanced type system extensions: rather, the type system extensions discover you! Nevertheless, it’s worthwhile to know what the tech tree for GHC’s type extensions are, so you can decide how much power (and the correspondingly headache inducing error messages) you need. I’ve organized the relations in the following diagram with the following criterion in mind:
- Some extensions automatically enable other extensions (implies);
- Some extensions offer all the features another extension offers (subsumes);
- Some extensions work really nicely with other extensions (synergy);
- Some extensions offer equivalent (but differently formulated) functionality to another extension (equiv).
It’s also worth noting that the GHC manual divides these extensions into “Extensions to data types and type synonyms”, “Class and instances declarations”, “Type families” and “Other type system extensions”. I have them organized here a little differently.
Our first tech tree brings together two extensions: arbitrary-rank polymorphism and generalized algebraic data types.
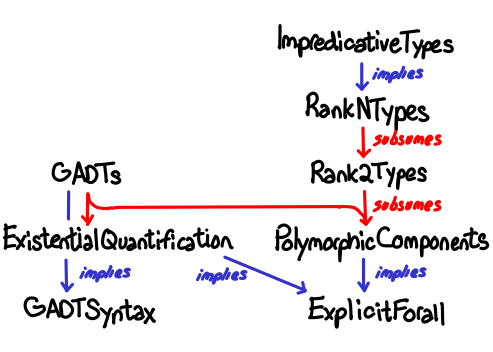
Briefly:
- GADTSyntax permits ordinary data types to be written GADT-style (with explicit constructor signatures):
data C where C :: Int -> C - ExplicitForall allows you to explicitly state the quantifiers in polymorphic types:
forall a. a -> a - ExistentialQuantification allows types to be hidden inside a data constructor:
data C = forall e. C e - GADTs permits explicit constructor signatures:
data C where C :: C a -> C b -> C (a, b). Subsumes ExistentialQuantification because existentially quantified data types are simply polymorphic constructors for which the type variable isn’t in the result. - PolymorphicComponents allows you to write
forall inside data type fields: data C = C (forall a. a) - Rank2Types allows polymorphic arguments:
f :: (forall a. a -> a) -> Int -> Int. This with GADTs subsumes PolymorphicComponents because data type fields with forall within them correspond to data constructors with rank-2 types. - RankNTypes:
f :: Int -> (forall a. a -> a) - ImpredicativeTypes allows polymorphic functions and data structures to be parametrized over polymorphic types:
Maybe (forall a. a -> a)
Our next tech tree deals with type class instances.
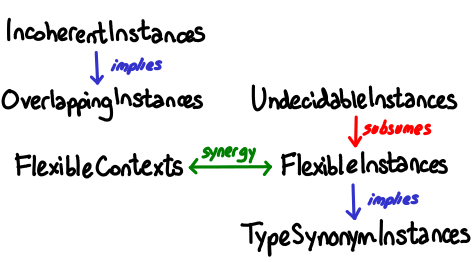
Briefly:
- TypeSynonymInstances permits macro-like usage of type synonyms in instance declarations:
instance X String - FlexibleInstances allows more instances for more interesting type expressions, with restrictions to preserve decidability:
instance MArray (STArray s) e (ST s) (frequently seen with multi-parameter type classes, which are not in the diagram) - UndecidableInstances allows instances for more interesting type expression with no restrictions, at the cost of decidability. See Oleg for a legitimate example.
- FlexibleContexts allows more type expressions in constraints of functions and instance declarations:
g :: (C [a], D (a -> b)) => [a] -> b - OverlappingInstances allows instances to overlap if there is a most specific one:
instance C a; instance C Int - IncoherentInstances allows instances to overlap arbitrarily.
Perhaps conspicuously missing from this diagram is MultiParamTypeClasses which is below.
Our final tech tree addresses programming with types:
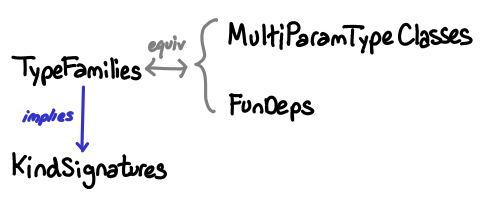
Briefly:
- KindSignatures permits stating the kind of a type variable:
m :: * -> * - MultiParamTypeClasses allow type classes to range over multiple type variables:
class C a b - FunDeps allow restricting instances of multi-parameter type classes, helping resolve ambiguity:
class C a b | a -> b - TypeFamilies allow “functions” on types:
data family Array e
The correspondence between functional dependencies and type families is well known, though not perfect (type families can be more wordy and can’t express certain equalities, but play more nicely with GADTs).
March 4, 2011A petri net is a curious little graphical modeling language for control flow in concurrency. They came up in this talk a few weeks ago: Petri-nets as an Intermediate Representation for Heterogeneous Architectures, but what I found interesting was how I could describe some common concurrency structures using this modeling language.
Here is, for example, the well venerated lock:
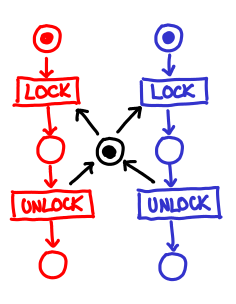
The way to interpret the graph is thus: each circle is a “petri dish” (place) that may contain some number of tokens. The square boxes (transitions) are actions that would like to fire, but in order to do so all of the petri dishes feeding into them must have tokens. It’s the sort of representation that you could make into a board game of sorts!
If multiple transitions can fire off, we pick one of them and only that one succeeds; the ability for a token to flow down one or another arrow encodes nondeterminism in this model. In the lock diagram, only one branch can grab the lock token in the middle, but they return it once they exit the critical area (unlock).
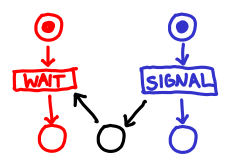
Here is a semaphore:
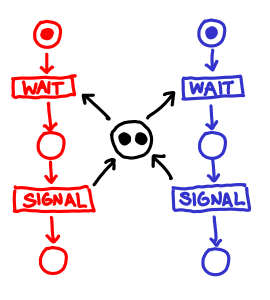
It’s exactly the same, except that the middle place may contain more than one token. Of course, no one said that separate processes must wait before signalling. We can implement a simple producer-consumer chain like this:
Note that petri net places are analogous to MVar (), though it takes a little care to ensure we are not manufacturing tokens out of thin air in Haskell, due to the lack of linear types. You may also notice that petri nets say little about data flow; we can imagine the tokens as data, but the formalism doesn’t say much about what the tokens actually represent.
March 2, 2011The bug bit me in early 2009, during MIT’s independent activities period; really, it was two bugs. The first was 6.184, the re-animated introductory computer science class taught in Scheme—for obvious reasons. But I don’t think that was sufficient: I seemed to recall thinking Scheme was interesting but not a language I actually wanted to code in. The second was a comment made by Anders Kaseorg after I finished delivering a talk Introduction to Web Application Security (one of the few things that, as a freshman at MIT, I thought I knew well enough to give a lecture on). One of the emphases of the talk was all about types: that is, the fact that “string” doesn’t adequately represent the semantic content of most bits of text that float around in our applications these days. Haskell came up as a way of making your compiler make sure you didn’t mix up HTML with plain text.
Something must have clicked. That February, I wrote:
Wow. Haskell is pretty.
To which someone replied:
Don’t look too hard into the sun, your eyes will get burned.
And thus a statically-typed functional programmer was born.
Postscript. My first application in Haskell was a Laplace solver, with which I also learned about monads (because a map lookup returned a Maybe value, and Anders decided it would be a good idea to talk about do-notation and bind to elucidate how to handle it. I probably didn’t understand the explanation the first time around, but I did manage to get the program working.)
February 28, 2011two inflammatory vignettes
The term to cargo cult is one with derogatory connotations: it indicates the act of imitating the superficial exterior without actually understanding the underlying causal structure of the situation. The implication is that one should try to understand what one is doing, before doing it. There is, however, an ounce of truth in the practice of cargo culting: when you are in a situation in which you legitimately do not know what’s going on (e.g. the context of an experiment), it is safest to preserve as many superficial traits as possible, in case a “superficial” trait in fact has a deep, non-obvious connection to the system being studied. But in this regard, beneficial “cargo culting” is nothing like the islanders throwing up airstrips in hopes of attracting planes—understanding what conditions are applicable for this treatment is often the mark of experience: the novice ignores conditions that should be preserved and does not know how to probe deeper.
Hacking is the art of accidental generalization. It is developing a program under a single set of conditions (a hard-coded test input, a particular directory structure, a single URL) and (perhaps) hoping it will work in the more general case. Anything that gets in the way of specificity—proofs, types, security, verbosity, edge-cases, thinking—is the enemy for pure creation. It is the art of the present, and much profit and pleasure can be derived from it. It is the art of laser precision, each problem dealt with as it comes. It is an art that becomes more acceptable engineering practice with experience: one develops little internal censors that continually pipe up with mental flags where you need to give a little extra to make the generalization work. Novices are recommended to bring their check-lists along.
February 25, 2011Most of my hacking cycles right now are going towards debugging the new code generator for GHC. The code generation stage of GHC takes the Spineless Tagless G-machine (STG) intermediate representation (IR) to the C– high-level assembly representation; the old code generator essentially performed this step in one big bang. The new code generator is many things. It is a more modular, understandable and flexible codebase. It is a client of cutting edge research in higher-order frameworks for control-flow optimization.
It is also frickin’ hard to debug.
I used to get frustrated and give up if I couldn’t figure out what was causing a bug within a few hours of close analysis. Working on GHC has enlightened me about the multi-day debugging: a well-defined bug that persists despite several days of intense analysis. (I’ve only managed this a few times in the past—I’m quite proud that I managed to pull together enough information to resolve “the bug”. What is “the bug”? Have you ever been browsing a MediaWiki site and then been mysteriously asked to download a PHP file? Yeah, that’s “the bug”). It has exponentially increased my proficiency with gdb and has been an amazing romp in the theoretics and practice of compiler construction. I’ve felt stupid for not immediately understanding what in retrospect seem perfectly clear and obvious concepts. I’ve felt an amazing rush, not from when the problem is solved (though that certainly gives a good feeling), but when my plan of attack is making progress. I’ve seen my theories evolve from one to another to another, and have learned never to trust any experimental observation at first sight.
While the debugging process is not yet done (though I think I’m close to having a correct—but slow—new code generation pipeline), I thought I’d take out some time to describe the journey.
There are some classic reasons:
- I didn’t write GHC. (Ha!) Debugging not-your-code is hard.
- I’ve never written a compiler before.
- In fact, I had never taken a compilers class (currently being fixed, though I think I’ve learned a lot more a lot more quickly via GHC hacking).
Some reasons that come naturally from big projects:
- GHC takes a long time to compile, so think before you compile.
- GHC is big; there are a lot of possible places for bugs to creep in.
Some of it’s because GHC is written in a functional programming language for compiling functional programs:
- Forget about line-by-line stepping: it’s all assembly and memory dumps.
- GHC is highly abstract, and you can’t really hope to understand what the code is doing by mapping it to some step-by-step execution.
- The generated code is in continuation passing style and doesn’t resemble any imperative execution scene you might have seen before. I will never again take a calling convention for granted.
Fascinatingly enough, while the bugs result in extremely strange behavior in compiled programs that takes ages to decipher, once the bad behavior is fully understood, the fix is usually a one-liner. It is this fact that makes debugging GHC frustrating and brilliant at the same time: sometimes code you’re debugging is fundamentally mistaken, and you have to rewrite the whole thing. GHC’s code is fundamentally clear (a testament to those who wrote it), and a bug is usually just a small detail someone forgot to attend to. The solutions are like Mystery Hunt solutions: short, and you know when you’ve found it. Nothing messy like, “What is this actually supposed to do?”
I have the benefit of an existing code generation pipeline which I can use to compare my results with, although doing so is not trivial since the new code generator does go about the compilation in a fundamentally different way, and so sections of code are frequently not comparable.
I also have the benefit of a wondrous test-suite which produces me programs that reproduceably segfault with little fuss, and have been relatively blessed with bugs that show in single-threaded situations. My programs have well defined inputs and outputs, and I have sophisticated mechanisms for inspecting the internal state of the multipass compiler.
- Have utter and complete confidence in your build. If you have the slightest suspicion that your build didn’t precisely pick up on a change you made, make a new build tree and build from scratch. A lot of mysterious problems go away when you do a clean build.
- The GHC .gdbinit file is magical; I don’t know where I’d be without it, and I’m probably only using 20% of its macros at this point.
disas is your friend, as is pstk and pmem. I can’t describe how many times I’ve used the go-back-in-time trick. - It is always worth reducing your test input. Not only does it make the output you stare at simpler, the act of reduction will cause changes in irrelevant portions of the output, but preserve the essential portions that are related to the bug. Probably my biggest breakthroughs were when I could show that another program exhibited the same bug.
- Do the background reading. A lot of the “undocumented” cleverness in GHC is actually described in the literature. Reading the Hoopl paper suddenly made the register spilling code lucid, and made me realize my princess was in another castle.
- Your first theory is usually wrong. You will fixate on the wrong detail. Keep all of the possibilities in mind, but at the very beginning, you should ask for more information. If you did not write the system, you probably don’t have any intuition about what the bug might be, and attempts to short-cut the analysis process will just leave you confused. (An annoying side effect is once you’ve done your research, you start thinking, “Man, if only I had known the system a bit better, I would have spotted that bug much more quickly.”)
- You still need a working theory to dictate what sort of information you are going to gather, but it’s really important to keep anomalies in mind as you begin to formulate a solution. For a more detailed analysis on this, see Test 4221 below. If a fix “works”, but there is an anomaly, keep trying to understand the situation.
- You will never collect a ton of data in one go, stare at it, and notice the critical pattern that resolves the bug. Debugging is all about asking the right questions, and on the path to this state, you will ask a lot of wrong questions.
Warning: Gory technical detail ahead.
My first job was to make the latest new code generation code compile with the latest GHC branch (it had bit-rotted a bit in the interim.) This went mostly smoothly, except for the fact that Norman Ramsey really likes polymorphic local definitions and MonoLocalBinds reared its ugly head in Hoopl and a few other modules.
Test 4030 was this “simple” program (simple is in quotes, because as Simon Peyton-Jones put it, “that looks like a hard one to start with… threads, exceptions, etc.”) :
main = do tid <- block $ forkIO $ let x = x in x
killThread tid
The resulting code segfaulted in stg_BLACKHOLE_info when attempting to dereference “something.” :
0x822a6e0 <stg_CAF_BLACKHOLE_info>: jmp 0x822a620 <stg_BLACKHOLE_info>
0x822a620 <stg_BLACKHOLE_info>: mov 0x4(%esi),%eax
0x822a623 <stg_BLACKHOLE_info+3>: test $0x3,%eax
0x822a628 <stg_BLACKHOLE_info+8>: jne 0x822a663 <stg_BLACKHOLE_info+67>
0x822a62a <stg_BLACKHOLE_info+10>: mov (%eax),%ecx -- SEGFAULT!
This something ended up being a new stack slot that Simon Marlow introduced when he had rewritten the blackholing scheme. The solution was to port these changes to the new code generator. I ended up manually reviewing every patch within the merge time window to ensure all changes had been ported, and probably squished a few latent bugs in the process. There’s no patch because I ended up folding this change into the merge (since the new blackholing scheme had not existed at the time the new code generator branch was frozen.)
Test ffi021 involved creating a pointer to an imported FFI function, and then dynamically executing it. (I didn’t even know you could do that with the FFI!) :
type Malloc = CSize -> IO (Ptr ())
foreign import ccall unsafe "&malloc" pmalloc:: FunPtr Malloc
foreign import ccall unsafe "dynamic" callMalloc :: FunPtr Malloc -> Malloc
This ended up being a latent bug in the inline statement optimizer (not a bug in the new code generator, but a bug that the new codegen tickled). I got as far as concluding that it was an optimization bug in the native code generator before Simon Marlow identified the bug, and we got a one-line patch. :
hunk ./compiler/cmm/CmmOpt.hs 156
- where infn (CmmCallee fn cconv) = CmmCallee fn cconv
+ where infn (CmmCallee fn cconv) = CmmCallee (inlineExpr u a fn) cconv
This one took three weeks to solve. The original test code was fairly complex and highly sensitive to code changes. My first theory was that we were attempting to access a variable that had never been spilled to the stack, but after talking to Simon Peyton Jones about how stack spilling worked I got the inkling that this might not actually be the problem, and stopped attempting to understand the Hoopl code that did spilling and went back to analysis. There was another false end with regards to optimization fuel, which I hoped would help pinpoint the point of error but in fact doesn’t work yet. (Optimization fuel allows you to incrementally increase the number of optimizations applied, so you can binary search which optimization introduces the bug. Unfortunately, you most of the so-called “optimizations” were actually essential program transformations on the way to machine code.)
The breakthrough came when I realized that the bug persisted when I changed the types in the input program from CDouble to CInt64, but not when I changed the types to CInt32. This allowed me to identify the erroneous C– code involving garbage collection and reduce the test-case to a very small program which didn’t crash but showed the wrong code (since the program needed to run for a while in order to trigger a stack overflow at precisely the right place):
{-# LANGUAGE ForeignFunctionInterface #-}
module Main(main) where
import Foreign.C
foreign import ccall safe "foo" foo :: CLLong -> CLLong
-- Changing to unsafe causes stg_gc_l1 to not be generated
-- Changing to IO causes slight cosmetic changes, but it's still wrong
main = print (foo 0)
After a huge misunderstanding regarding the calling convention and futile attempts to find a bug in the stack layout code (I assumed that slot<foo> + 4 indicated a higher memory location; in fact it indicated a lower memory location than slot<foo>), I finally identified the problem to be with the stg_gc_* calling convention.
My first patch to fix this changed the callee (the stg_gc_* functions) to use the observed calling convention that the new code generator was emitting, since I couldn’t see anything wrong with that code. But there was an anomalous bit: by this theory, all of the calls to GC should have used the wrong calling convention, yet only doubles and 64-bit integers exhibited this behavior. My patch worked, but there was something wrong. This something wrong was in fact the fact that 32-bit x86 has no general purpose non-32-bit registers, which was why the code generator was spilling only these types of arguments onto the stack. I learned a little bit more about GHC’s virtual registers, and determined another one line fix. :
hunk ./compiler/cmm/CmmCallConv.hs 50
- (_, GC) -> getRegsWithNode
+ (_, GC) -> allRegs
This one is in progress. Fixing the GC bug resolved all of the remaining mysterious test suite failures (hooray), and with this I was able to recompile GHC with all of the libraries with the new code generator. This triggered test 2047 to start segfaulting.
It took me a little bit of time to establish that I had not introduced a bug from compiling the stage 2 compiler with the new codegen (which I had done overzealously) and confirm which library code had the bug, but once I had done so I managed to reduce it to the following program (which I had lovingly named “bagels”):
import Bagel
main = do
l <- getContents
length l `seq` putStr (sort l)
with sort defined in the module Bagel as such:
module Bagel where
-- a bastardized version of sort that still exhibits the bug
sort :: Ord a => [a] -> [a]
sort = mergeAll . sequences
where
sequences (a:xs) = compare a a `seq` []:sequences xs
sequences _ = []
mergeAll [x] = x
mergeAll xs = mergeAll (mergePairs xs)
mergePairs (a:b:xs) = merge a b: mergePairs xs
mergePairs xs = xs
merge (a:as') (b:bs') = compare a a `seq` merge as' as'
merge _ _ = []
and run with the following data:
$ hexdump master-data
0000000 7755 7755 7755 7755 7755 7755 7755 7755
*
000b040
This program has a number of curious properties. The segfault goes away if I:
- Turn off compacting GC
- Reduce the size of master-data
- Turn off optimizations
- Use the old codegen
- Put all of the code in one file
- Remove the seqs from ‘sort’ (which isn’t actually a sort)
- Remove the seqs from ‘main’
- Make the sort function monomorphic on Char
The current theory is someone (either the new code generator or the compacting GC) is not handling a tag bit properly, but I haven’t quite figured out where yet. This is the only outstanding bug unique to the new code generator.
The code generator produces some pretty idiotic code (as I noticed while I was reading pages and pages of C–), and it’s also pretty slow. Once correct, it’s time to optimize, in more ways than one.
February 23, 2011In his book Against Method, Paul Feyerabend writes the following provocative passage about ‘ad hoc approximations’, familiar to anyone whose taken a physics course and thought, “Now where did they get that approximation from…”
The perihelion of Mercury moves along at a rate of about 5600" per century. Of this value, 5026" are geometric, having to do with the movement of the reference system, while 531" are dynamical, due to the perturbations in the solar system. Of these perturbations all but the famous 43" are accounted for by classical mechanics. This is how the situation is usually explained.
The explanation shows that the premise from which we derive 43" is not the general theory of relativity plus suitable initial conditions. The premise contains classical physics in addition to whatever relativistic assumptions are being made. Furthermore, the relativistic calculation, the so-called ‘Schwarzschild solution’, does not deal with the planetary system as it exists in the real world (i.e. our own asymmetric galaxy); it deals with the entirely fictional case of a central symmetrical universe containing a singularity in the middle and nothing else. What are the reasons for employing such an odd conjunction of premises?
The reason, according to the customary reply, is that we are dealing with approximations. The formulae of classical physics do not appear because relativity is incomplete. Nor is the centrally symmetric case used because relativity does not offer anything better. Both schemata flow from the general theory under special circumstances realized in our planetary system provided we omit magnitudes too small to be considered. Hence, we are using the theory of relativity throughout, and we are using it in an adequate matter.
Note, how this idea of an approximation differs from the legitimate idea. Usually one has a theory, one is able to calculate the particular case one is interested in, one notes that this calculation leads to magnitudes below experimental precision, one omits such magnitudes, and one obtains a vastly simplified formalism. In the present case, making the required approximations would mean calculating the full n-body problem relativistically (including long-term resonances between different planetary orbits), omitting magnitudes smaller than the precision of observation reached, and showing that the theory thus curtailed coincides with classical celestial mechanics as corrected by Schwarzschild. This procedure has not been used by anyone simply because the relativistic n-body problem has as yet withstood solution. There are not even approximate solutions for important problems such as, for example, the problem of stability (one of the first great stumbling blocks for Newton’s theory). The classical part of the explanans [the premises of that explain our observations], therefore, does not occur just for convenience, it is absolutely necessary. And the approximations made are not a result of relativistic calculations, they are introduced in order to make relativity fit the case. One may properly call them ad hoc approximations.
Feyerabend is wonderfully iconoclastic, and I invite the reader to temporarily suspend their gut reaction to the passage. For those thinking, “Of course that’s what physicists do, otherwise we’d never get any work done,” consider the question, Why do we have any reason to believe that the approximations are justified, that they will not affect the observable results of our calculations, that they actually reflect reality? One could adopt the viewpoint that such doubts are unproductive and get in the way of doing science, which we know from prior experience to work. But I think this argument does have important implications for prescriptivists in all fields—those who would like to say how things ought to be done (goodness one sees a lot of that in the software field; even on this blog.) Because, just as the student complains, “There is no way I could have possibly thought up of that approximation” or the mathematician winces and thinks “There is no reason I should believe that approximation should work”, if these approximations do exist and the course of science is to discover them, well, how do you do that?
The ivory tower is not free of the blemishes of real life, it seems.
February 21, 2011When programmers automate something, we often want to go whole-hog and automate everything. But it’s good to remember there’s still a place for manual testing with machine assistance: instead of expending exponential effort to automate everything, automate the easy bits and hard-code answers to the hard research problems. When I was compiling the following graph of sources of test data, I noticed a striking polarization at the ends of “automated” and “non-automated.”
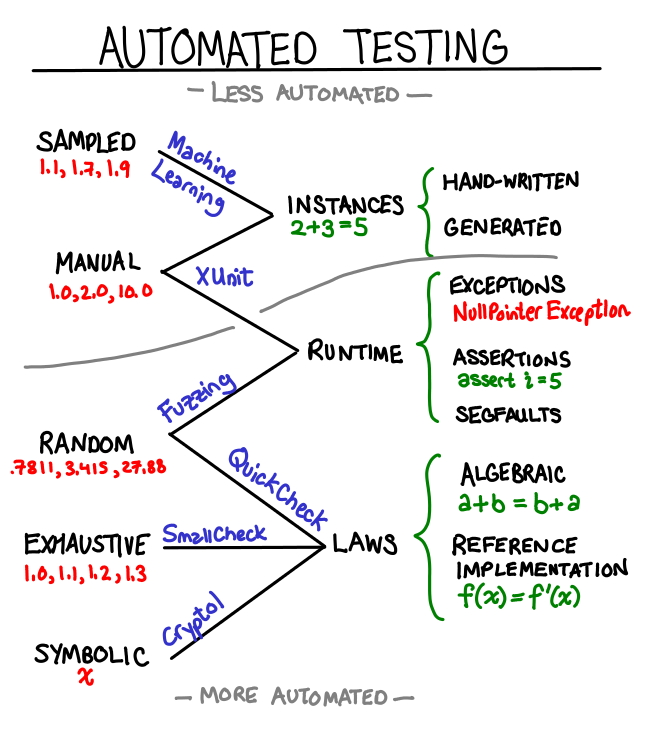
An ideal test framework would support combining all of these data sources and all of these testing mechanisms. Some novel approaches include:
- Randomly generated test-cases with manual verification. Obviously you won’t be able to hand verify thousands of test-cases, but a few concrete examples can do wonders for documentation purposes, and random generation prevents us from only picking “nice” inputs.
- Reference implementation as previous version of the code. To the limit, you automatically accept the output of an old implementation and save it to your test suite, and when a test starts failing you the framework asks you to check the output, and if it’s “better” than before you overwrite the old test data with the new. GHC’s test suite has something along these lines.
- You’ve written lots of algebraic laws, which you are using Quickcheck to verify. You should be able to swap out the random generator with a deterministic stream of data from a sampled data source. You’d probably want a mini-DSL for various source formats and transforming them into your target representation. This also works great when you’ve picked manual inputs, but exactly specifying the output result is a pain because it is large and complicated. This is data-driven testing.
- Non-fuzzing testing frameworks like Quickcheck and Smallcheck are reasonably good at dealing with runtime exceptions but not so much with more critical failures like segmentation faults. Drivers for these frameworks should take advantage of statelessness to notice when their runner has mysteriously died and let the user know the minimal invocation necessary to reproduce the crash—with this modification, these frameworks subsume fuzzers (which are currently built in an ad hoc fashion.)
It would be great if we didn’t have to commit to one testing methodology, and if we could reuse efforts on both sides of the fence for great victory.
February 20, 2011To: Oliver Charles
Subject: [Haskell-cafe] Please review my Xapian foreign function interface
Thanks Oliver!
I haven’t had time to look at your bindings very closely, but I do have a few initial things to think about:
- You’re writing your imports by hand. Several other projects used to do this, and it’s a pain in the neck when you have hundreds of functions that you need to bind and you don’t quite do it all properly, and then you segfault because there was an API mismatch. Consider using a tool like c2hs which rules out this possibility (and reduces the code you need to write!)
- I see a lot of unsafePerformIO and no consideration for interruptibility or thread safety. People who use Haskell tend to expect their code to be thread-safe and interruptible, so we have high standards ;-) But even C++ code that looks thread safe may be mutating shared memory under the hood, so check carefully.
I use Sup, so I deal with Xapian on a day-to-day basis. Bindings are good to see.
Cheers,
Edward
February 18, 2011Checked exceptions are a much vilified feature of Java, despite theoretical reasons why it should be a really good idea. The tension is between these two lines of reasoning:
Well-written programs handle all possible edge-cases, working around them when possible and gracefully dying if not. It’s hard to keep track of all possible exceptions, so we should have the compiler help us out by letting us know when there is an edge-case that we’ve forgotten to handle. Thus, checked exceptions offer a mechanism of ensuring we’ve handled all of the edge-cases.
and
Frequently checked exceptions are for error conditions that we cannot reasonably recover from close to the error site. Passing the checked exception through all of the intervening code requires each layer to know about all of its exceptions. The psychological design of checked exceptions encourages irresponsible swallowing of exceptions by developers. Checked exceptions don’t scale for large amounts of code.
In this post, I suggest another method for managing checked exceptions: prove that the code cannot throw such an exception.
“Prove that the code cannot throw an exception?” you might say. “Impossible! After all, most checked exceptions come from the outside world, and surely we can’t say anything about what will happen. A demon could just always pick the worst possible scenario and feed it into our code.”
My first answer to the skeptic would be that there do indeed exist examples of checked exceptions that happen completely deterministically, and could be shown to be guaranteed not to be thrown. For example, consider this code in the Java reflection API:
Object o, Field f; // defined elsewhere
f.setAccessible(true);
f.get(o);
The last invocation could throw a checked exception IllegalAccessException, but assuming that the setAccessible call did not fail (which it could, under a variety of conditions), this exception cannot happen! So, in fact, even if it did throw an IllegalAccessException, it has violated our programmer’s expectation of what the API should do and a nice fat runtime error will let us notice what’s going on. The call to setAccessible discharges the proof obligation for the IllegalAccessException case.
But this may just be an edge case in a world of overwhelmingly IO-based checked exceptions. So my second answer to the skeptic is that when we program code that interacts with the outside world, we often don’t assume that a demon is going to feed us the worst possible input data. (Maybe we should!) We have our own internal model of how the interactions might work, and if writing something that’s quick and dirty, it may be convenient to assume that the interaction will proceed in such and such a manner. So once we’ve written all the validation code to ensure that this is indeed the case (throwing a runtime exception akin to a failed assert if it’s not), we once again can assume static knowledge that can discharge our proof obligations. Yes, in a way it’s a cop out, because we haven’t proved anything, just told the compiler, “I know what I’m doing”, but the critical extra is that once we’ve established our assumptions, we can prove things with them, and only need to check at runtime what we assumed.
Of course, Java is not going to get dependent types any time soon, so this is all a rather theoretical discussion. But checked exceptions, like types, are a form of formal methods, and even if you don’t write your application in a dependently typed language, the field can still give useful insights about the underlying structure of your application.
The correspondence between checked exceptions and proofs came to me while listening to Conor McBride’s lecture on the Outrageous Arrows of Fortune. I hope to do a write up of this talk soon; it clarified some issues about session types that I had been thinking about.
I consulted the following articles when characterizing existing views of Java checked exceptions.
February 16, 2011Hoopl is a “higher order optimization library.” Why is it called “higher order?” Because all a user of Hoopl needs to do is write the various bits and pieces of an optimization, and Hoopl will glue it all together, the same way someone using a fold only needs to write the action of the function on one element, and the fold will glue it all together.
Unfortunately, if you’re not familiar with the structure of the problem that your higher order functions fit into, code written in this style can be a little incomprehensible. Fortunately, Hoopl’s two primary higher-order ingredients: transfer functions (which collect data about the program) and rewrite functions (which use the data to rewrite the program) are fairly easy to visualize.








