ezyang's blog

The Cryptography of Bitcoin

It is actually surprisingly difficult for a layperson to find out precisely what cryptography Bitcoin uses, without consulting the source of Bitcoin directly. For example, the opcode OP_CHECKSIG, ostensibly checks the signature of something… but there is no indication what kind of signature it checks! (What are opcodes in Bitcoin? Well it turns out that the protocol has a really neat scripting system built in for building transactions. You can read more about it here.) So in fact, I managed to get some factual details wrong on my post Bitcoin is not decentralized, which I realized when commenter cruzer claimed that a break in the cryptographic hash would only reduce mining difficulty, and not allow fake transactions.

So I did my research and cracked open the Bitcoin client source code. The short story is that the thrust of my argument remains the same, but the details of a hypothetical attack against the cryptographic function are a bit more complicated—a simple chosen-prefix collision attack will not be sufficient. The long story? Bitcoin makes some interesting choices of the cryptography it chooses, and the rest of this post will explore those choices. Bitcoin makes use of two hashing functions, SHA-256 and RIPEMD-160, but it also uses Elliptic Curve DSA on the curve secp256k1 to perform signatures. The C++ implementation uses a local copy of the Crypto++ library for mining, and OpenSSL for normal usage. At the end of this post, you should have a better understanding of how Bitcoin employs cryptography to simulate the properties of currency.

Signatures in Bitcoin

In many ways, this is the traditional cryptography in Bitcoin. We ask the question, “How do we know that Alice was authorized to transfer 100 Bitcoins to Bob,” and anyone who has used public-key cryptography knows the answer is, “Alice signs the transaction with her private key and publishes this signature for the Bitcoin network to verify with her public key.” This signature is performed on the secp256k1 elliptic curve (key.h):

CKey()
{
    pkey = EC_KEY_new_by_curve_name(NID_secp256k1);
    if (pkey == NULL)
        throw key_error("CKey::CKey() : EC_KEY_new_by_curve_name failed");
    fSet = false;
}

Bitcoin community has discussed the choice of elliptic curve, and it appears this particular one was chosen for possible future speed optimizations.

Like all public cryptography systems, however, Bitcoin does not sign the entire transaction message (that would be far too expensive); rather, it signs a cryptographic hash of the message (script.cpp):

uint256 SignatureHash(CScript scriptCode, const CTransaction& txTo,
                      unsigned int nIn, int nHashType)
{
    // ...
    // Serialize and hash
    CDataStream ss(SER_GETHASH);
    ss.reserve(10000);
    ss << txTmp << nHashType;
    return Hash(ss.begin(), ss.end());
}

This hash is a double application of SHA-256:

template<typename T1>
inline uint256 Hash(const T1 pbegin, const T1 pend)
{
    static unsigned char pblank[1];
    uint256 hash1;
    SHA256((pbegin == pend ? pblank : (unsigned char*)&pbegin[0]), (pend - pbegin) * sizeof(pbegin[0]), (unsigned char*)&hash1);
    uint256 hash2;
    SHA256((unsigned char*)&hash1, sizeof(hash1), (unsigned char*)&hash2);
    return hash2;
}

Great, so how do we break this? There are several ways:

• We could break the underlying elliptic curve cryptography, by either solving the discrete logarithm problem (this is something quantum computers can do) or by breaking the particular elliptic curve that was chosen. Most research in this area goes towards finding vulnerabilities in specific elliptic curves, so the latter is more likely.
• We could break the underlying cryptographic hash function. In this case, we have a known signature from the user we would like to attack, and we generate another input transaction that hashes to the same value, so we can replay the previous signature. Such an attack would be dependent on the form of the serialized transaction that Bitcoin processes: it does a nontrivial amount of processing on a transaction, so some legwork by the attackers would be necessary; however, because transactions include a scripting system which permits complex transactions to be built, an attacker would have some leeway in constructing such an input. This would not work on single-use addresses, since no such signature exists for replay.

Breaking the signing algorithm requires a selective forgery attack or stronger, and means that arbitrary transactions may be forged and entered into the system. It would be a complete system break. For the signature replay attack, some protection could be gained by adding client-side checks that the same signature is never used for two different transactions.

Hashing in Bitcoin

This is the technically novel use of cryptography in Bitcoin, and it is used to answer the question, “With only traditional signatures, Alice can resend bitcoins she doesn’t actually have as many times as she wants, effectively creating multiple branches of a transaction tree. How do we prevent this?” The answer Bitcoin provides is, “Transaction chains are certified by the solution of a computationally hard problem (mining), and once a transaction is confirmed by its inclusion in a block, clients prefer the transaction chain that has the highest computational cost associated with it, invalidating any other spending on other branches.” Even if you don’t believe in decentralized currency, you have to admit, this is pretty elegant.

In more detail, the computationally hard problem is essentially a watered-down version of the first-preimage attack on a hash function. Miners are given a set of solution hashes (the hash of all zeros to a target hash), and are required to find a message with particular structure (a chain of blocks plus a nonce) that hashes to one of these hashes.

In this case, it is easy to see that a first-preimage attack on a hash function (or perhaps a slightly weaker) attack means that this hashing problem can be solved much more quickly. This is a security break if an adversary knows this method but no one in the network does; he can easily then capture more than 50% of the network’s computing capacity and split the block chain (Remember: this is exponential leverage. I don’t care how many teraflops of power the Bitcoin network has—smart algorithms always win.) In a more serious break, he can rewrite history by reconstructing the entire block chain, performing enough “computational work” to convince other clients on the network that his history is the true one. This attack scenario is well known and is described here. Note that once the method is widely disseminated and adopted by other miners, the computational power imbalance straightens out again, and the difficulty of the hashing problem can be scaled accordingly.

Addresses in Bitcoin

Similar to systems like PGP, Bitcoin users generate public and private keypairs for making signatures, but also publish a convenient “fingerprint”, actually a RIPEMD-160 hash for people to utilize as an identifier for a place you may send Bitcoin to (util.h):

inline uint160 Hash160(const std::vector<unsigned char>& vch)
{
    uint256 hash1;
    SHA256(&vch[0], vch.size(), (unsigned char*)&hash1);
    uint160 hash2;
    RIPEMD160((unsigned char*)&hash1, sizeof(hash1), (unsigned char*)&hash2);
    return hash2;
}

Unlike systems like PGP, Bitcoin has no public key distribution mechanism: the RIPEMD-160 hash is canonical for a public key. As such, if a collision is discovered in this key space, someone could spend Bitcoins from someone else’s address. This attack scenario is described here. This attack is mitigated by the fact that Bitcoin users are encouraged to use many addresses for their wallet, and that other uses of such collision-power may be more profitable for the attacker (as described above.)

Conclusion

As we can see, multiple different cryptographic primitives are used in ensemble in order to specify the Bitcoin protocol. Compromise of one primitive does not necessarily carry over into other parts of the system. However, all of these primitives are hard-coded into the Bitcoin protocol, and thus the arguments I presented in my previous essay still hold.

Bitcoin is not decentralized

Bitcoin was designed by Satoshi Nakamoto, and the primary client is developed by a bunch of folks at bitcoin.org. Do you care who these people are? In theory, you shouldn’t: all they do is develop an open source client for an open source protocol. Anyone else can develop their own client (and some people have) and no one, save the agreement of everyone in the Bitcoin network, can change the protocol. This is because the Bitcoin network is designed to be decentralized.

If you believe in the long term viability of Bitcoin, you should care who these people are. While Bitcoin itself is decentralized, the transition from Bitcoin to a new currency cannot be. This transition is guaranteed by the fact that all cryptosystems eventually become obsolete. Who will decide how this new currency is structured? Likely the original creators of Bitcoin, and if you have significant holdings in Bitcoin, you should care who these people are.

The following essay will flesh out this argument more carefully, as follows:

1. Cryptosystems, including cryptographic hashes, must be used with the understanding that they must eventually be replaced. One might argue that “If Bitcoin’s cryptography is broken, the rest of the financial industry is in trouble too”—we explain why this is irrelevant for Bitcoin. We also see why it’s reasonable to expect Bitcoin, if it becomes a serious currency, to stick around a long enough timespan for this obsolescence to occur.
2. There are several rough transition plans circulating the Bitcoin community. We describe the most common decentralized and the most common centralized variant, and explain why the decentralized variant cannot work in a non-disruptive manner, appealing both to economics and existing markets which have similar properties.
3. We more carefully examine the implications of these decentralized and centralized transitions, and assess the risk of the transition, in comparison to the other risks facing Bitcoin as a fledgling currency. We suggest that, while the transition of Bitcoin is not a central concern, the idea of naive decentralization is a myth that needs to be dispelled.

I’ve divided the essay into sections so that readers who are interested in specific sections of the argument. Feel free to skip around.

The cryptosystem time bomb

“All cryptosystems eventually become obsolete.” Compared to currency, cryptographic hashes are a relatively recent invention, dating only as far back as the 1970s. MD5 was invented in 1991, and it only took about a decade and a half to thoroughly break it. For computer programmers, the shifting landscape of cryptography is a given, and systems are designed with this in mind. Consider, for example, SSL certificates, which are used to secure many transactions on the Internet, including financial transactions. These need to be renewed every few years, and as new certificates are issued, their level of protection can be increased, to use newer ciphers or longer key sizes. Most current uses of cryptography follow this pattern: the ciphers and keys can be replaced with relative ease.

Bitcoin, however, is special. The way it achieves decentralization is by embedding all of its relevant technical details in the protocol. Among these is the hashing algorithm, SHA-256. It is literally impossible to “change” the hashing algorithm in Bitcoin; any change would constitute a change in the protocol, and thus result in a completely new currency. Don’t believe anyone who tells you otherwise. The argument “If Bitcoin’s cryptography is broken, the rest of the financial industry is in trouble too” is irrelevant, because other financial institutions have central control of the ciphers they use and can easily change them: Bitcoin cannot. And due to the possibility of weaknesses in SHA-1 spilling into the SHA-2 family (among which SHA-256 is a member), a competition for SHA-3 is already being held.

Will Bitcoin last long enough for fraudulent transactions to become practical? It may not (after all, there are many other possible problems with the currency that may kill it off before it ever gets to this stage.) However, if it does become established, you can expect it to be a hardy little bastard. Currencies stick around for a long time.

Decentralized and centralized currency transition

The Bitcoin community has realized the fact that a transition will become necessary, and though the general sense is that of, “We’ll figure it out when we get there,” there have been some vague proposals floated around. At the risk of constructing strawmen, I would like to now present my perception of the two most popularly voiced plans. First, the decentralized plan:

Because cryptosystems don’t break overnight, once the concern about SHA-256 becomes sufficiently high we will create a new version of Bitcoin that uses a stronger cryptographic hash. We will then let the market decide an exchange rate between these two currencies, and let people move from one to the other.

This is decentralized because anyone can propose a new currency: the market will decide which one will win out in the end. It also cannot possibly work in a nondisruptive manner, for the simple reason that anyone seeking to exchange the old Bitcoin for the new one will have to find a willing buyer, and at some point, hyperinflation will ensure that there are no willing buyers. All existing Bitcoins will then be worthless.

At this point, we’ll take a short detour into the mooncake black market, a fascinating “currency” in China that has many similar properties to an obsolescing Bitcoin. The premise behind this market is that, while giving cash bribes are illegal, giving moon cake vouchers are not. Thus, someone looking to bribe someone can simply “gift” them a moon cake voucher, which is then sold on the black market to be converted back into cash.

Those partaking in the moon cake black market must be careful, because once the Autumn Festival arrives, all of these vouchers must be exchanged for moon cakes or become worthless. As the date arrives, you see an increasingly frenzied game of hot potato for the increasingly devalued vouchers. The losers? They end up with lots of moon cakes. There is of course one critical difference, which is that the losers of the Bitcoin game are left with nothing at all.

Is this a transition? Yes. Is it disruptive? Definitely yes. It is certainly not what you want a currency you’re using for every day transactions to be doing. Of course, this may be acceptable risk for some industries, and we’ll analyze this more in the last section.

Here is the centralized plan:

Once the concern for the hashing algorithm is high enough, we will create a new Bitcoin protocol. This protocol will not only include a new hashing algorithm, but also be based off of the value of the old Bitcoin economy at some date: at that point, all newer transactions are invalid in the new Bitcoin scheme, and that snapshot is used to determine the amount of Bitcoins everyone has.

There is a variant, which deals with the case when active attacks are being carried out against the hashing algorithm before they have managed to switch, which involves marking specific block chains as known good, and zeroing out suspected fraudulent transactions.

Is this plan really centralized? Yes: someone needs to design the new protocol, to convince all the clients to buy into it, and to uniformly switch over to the new economy when the day arrives. The fragmentation of the Bitcoin economy would be extremely disruptive and not in the best interests of any of the main players. Any other changes to the Bitcoin protocol (and at this point, there probably would be many proposals) could have massive implications for the Bitcoin economy.

Implications and risk

Here, we assess the question, “Do I really care?” In the short term, no. Bitcoin has many, many weaknesses that it will be tested against. Though I personally hope it will succeed (it is certainly a grand experiment that has never been carried out before), my assessment is that its chances are not good. Worrying excessively about the transition is not a good use of time.

However, this does not mean that it is not an important fact to remember. The future of Bitcoin depends on those who will design its successor. If you are investing substantially in Bitcoin, you should at the very least be thinking about who has the keys to the next kingdom. A more immediate issue are the implications of a Bitcoin client monoculture (one could push out an update that tweaks the protocol for nefarious purposes). Those using Bitcoin should diversify their clients as soon as possible. You should be extremely skeptical of updates which give other people the ability to flip your client from one version of the protocol to another. Preserve the immutability of the protocol as much as possible, for without it, Bitcoin is not decentralized at all.

Thanks to Nelson Elhage, Kevin Riggle, Shae Erisson and Russell O’Connor for reading and commenting on drafts of this essay.

Update. Off-topic comments will be ruthlessly moderated. You have been warned.

Update two. One possible third succession plan that has surfaced over discussion at Hacker News and Reddit is the decentralized bootstrapped currency. Essentially, multiple currencies compete for buy-in and adoption, but unlike the case of two completely separate currencies separated only by an exchange rate, these currencies are somehow pegged to the old Bitcoin currency (perhaps they reject all Bitcoin transactions after some date, or they require some destructive operation in order to convert an old Bitcoin into a new one—the latter may have security vulnerabilities.) I have not analyzed the economic situation in such a case, and I encourage someone else to take it up. My hunch is that it will still be disruptive; perhaps even more so, due to the artificial pegging of the currency.

Chain Rule + Dynamic Programming <br />= Neural Networks

(Guess what Edward has in a week: Exams! The theming of these posts might have something to do with that…)

At this point in my life, I’ve taken a course on introductory artificial intelligence twice. (Not my fault: I happened to have taken MIT’s version before going to Cambridge, which also administers this material as part of the year 2 curriculum.) My first spin through 6.034 was a mixture of disbelief at how simple the algorithms were, indignation at their examination methods, and the vague sense at the end that I really should have paid more attention. My second time through, I managed to distill a lot more algorithmic content out of the course, since I wasn’t worrying as much about the details.

The topic of today’s post is one such distillation of algorithmic content from the neural network learning process. Well, at least, for multilayer perceptrons—since that’s what usually gets studied as a case of neural networks. It should be noted that the perceptron is a really simple sort of mathematical function: it’s a multivariable function that takes as arguments a weight vector and an input vector, takes their dot product and runs the result through an activation function (which is usually chosen so that it has nice properties when differentiated.) “Learning” in this case is first-order optimization via gradient descent, and the primarily computational content involves calculating the partial derivative of the function with respect to the weight vector—something that anyone who has taken multivariable calculus ought to be able to do in his sleep.

Note that I say ought. Actually, neural networks gave me a pretty horrendous time both times I had to learn it. Part of the trouble is that once you’ve worked out the update formulas, you don’t actually need to understand the derivation: they “just work.” Of course, no self-respecting course would want to quiz you on your ability to memorize the relevant equations, so they’ll usually ask you to write out the derivation. There you run into the second trouble: most presentations of the derivation are quite long and don’t “compress” well.

The first insight into the process, which I (eventually) picked up the first time I took the course, was that these derivations were actually just repeatedly applying the chain rule. Thus, the laborious analysis of all of the partial derivatives can be replaced with the following algorithm: “Chop the perceptron into smaller functions, calculate the derivative of each function, and then multiply the results back together.” Now, this does require a little bit of care: one normally visualizes the perceptron network as a function on the input values, but the derivative is with respect to the weights. Furthermore, the perceptron network is a much more involved partial differentiation problem than one usually finds on a multivariable calculus exam, so if you don’t have your variable indexing sorted out it’s very easy to get confused. (Here, a notion of fresh names and global names comes in handy, because it sets the ground rules for notational sleights of hands that mathematicians do freely and confusingly.) If you have the chain rule in your arsenal, you have a fairly convincing story for the output perceptron, and with a little bit more confusion you might manage the the internal perceptrons too.

The second insight into the process I didn’t pick up until my second time around: it is the resemblance of backpropagation to dynamic programming. This involved the realization that, in principle, I could calculate the partial derivative of the function with respect to any weight simply by tracing out the nodes “downstream” from it, and calculating the (longer) derivative chains manually. I could do this for every node, although it might get a bit tedious: the key idea of “backpropagation” is that you can reuse results for an efficiency increase, just as you do for dynamic programming. It is also gratifying to see that this explains why both treatments I’ve seen of neural nets obsess over δ, a seemingly innocuous derivative that really shouldn’t get its own symbol. The reason is this value is precisely what is stored in the dynamic programming table (in this case, shaped the same way as the input neural net); the actual partial derivative for a weight isn’t actually what we need. This is actually fairly common, as far as contest dynamic programming problems go—part of the trick is figuring out what intermediate calculations you also need to store in your table. Backpropagation is then just filling out the table from the output node to the input nodes.

So there you have it: chain rule + dynamic programming = neural network backpropagation algorithm. Of course, this formulation requires you to know how to do the chain rule, and know how to do dynamic programming, but I find these concepts much easier to keep in my brain, and their combination pleasantly trivial.

Postscript. No lecturer can resist the temptation to expound on what they think “artificial intelligence” is. I’ll take this opportunity to chime in: I believe that AI is both a problem and an approach:

• Artificial intelligence is a problem, insofar as asking the question “What can humans do that computers cannot” is a tremendous way of digging up computationally interesting problems, and
• Artificial intelligence is an approach, insofar as instances of intelligence in nature suggest possible solutions to computational problems.

I have tremendous respect for the power of AI to frame what questions researchers should be asking, and if we say an approach is AI because it handles a problem in this domain quite well, AI is everywhere. (It also explains why AI thrives at MIT, a very engineering oriented school.) I am still, however, skeptical about “biological inspiration”, since these approaches doesn’t actually seem to work that well (e.g. the fall of “traditional” AI and the rise of statistical NLP methods), and the fact that the resulting methods are a far cry from their biological counterparts, as any neuroscientist who is familiar with “neural” networks may attest. In some cases, the biological analogies may be actively harmful, obscuring the core mathematical issues.

An insufficiently lazy map

Another common thunk leak arises from mapping functions over containers, which do not execute their combining function strictly. The usual fix is to instead use a strict version of the function, ala foldl' or insertWith', or perhaps using a completely strict version of the structure. In today’s post, we’ll look at this situation more closely. In particular, the questions I want to answer are as follows:

1. Why do we need to create strict and lazy versions of these functions—why can’t these leaks be fixed by the user adding appropriate bang-patterns to some functions?
2. Though introducing a stricter API is usually the correct fix, in some circumstances, the problem is not that the API is insufficiently strict, but that the data structure is too insufficiently lazy (that is, inappropriately spine strict.) That is to say, what do I mean by an insufficiently lazy map?
3. For data structures in which spine-strictness is necessary, is there any reason that this strictness should not extend to the values themselves? I want to argue that in fact, all spine strict data structures should also be value strict. This may be a bit controversial.

Example

Our example is a very simple data structure, the spine-strict linked list:

data SpineStrictList a = Nil | Cons a !(SpineStrictList a)
ssFromList [] l = l
ssFromList (x:xs) l = ssFromList xs (Cons x l)
ssMap _ Nil l = l
ssMap f (Cons x xs) l = ssMap f xs (Cons (f x) l)

main = do
    let l = ssFromList ([1..1000000] :: [Int]) Nil
        f x = ssMap permute x Nil
    evaluate (f (f (f (f (f (f (f (f l))))))))

permute y = y * 2 + 1

We first create an instance of the data structure using the ssFromList, and then we perform a map over all of its elements using ssMap. We assume the structure of the list is not semantically important (after all, the distribution of trees in an opaque data structure is of no interest to the user, except maybe for performance reasons. In fact, ssFromList and ssMap reverse the structure whenever they’re called, in order to avoid stack overflows.) The space leak here exemplifies the classic “non-strict container function” problem, where a call to a function like map looks harmless but actually blows up.

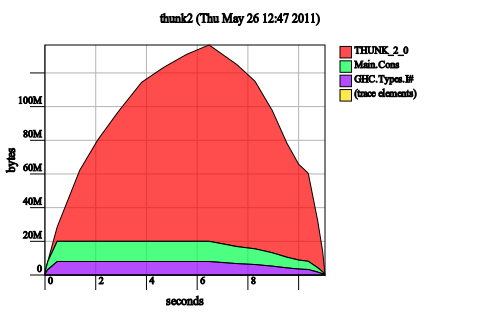
If you look at the implementation, this is not too surprising, based on a cursory look at SpineStrictList: of course it will accumulate thunks since it is not strict in the values, only the structure itself. Let’s look at some of the fixes.

Fixes

Bang-pattern permute. This fix is tempting, especially if you were thinking of our last example:

permute !y = y * 2 + 1

But it’s wrong. Why is it wrong? For one thing, we haven’t actually changed the semantics of this function: it’s already strict in y! The resulting seq is too deeply embedded in the expression; we need permute y to be invoked earlier, not y. Also, remember that fixing our combining function last time only worked because we managed to enable a GHC optimization which unboxed the tuples, avoiding allocating them at all. However, that won’t work here, because we have a strict data structure which GHC doesn’t know if it can get rid of, so all of the allocation will always happen.

Rnf the structure on every iteration. This works, but is pretty inelegant and inefficient. Essentially, you end up traversing every time, for ultimately quadratic runtime, just to make sure that everything is evaluated. rnf is a pretty heavy hammer, and it’s generally a good idea to avoid using it.

Use a strict version of ssMap. This is a pretty ordinary response that anyone who has every changed a function from foo to the foo' version has learned to try:

ssMap' _ Nil l = l
ssMap' f (Cons x xs) l = ssMap' f xs ((Cons $! f x) l)

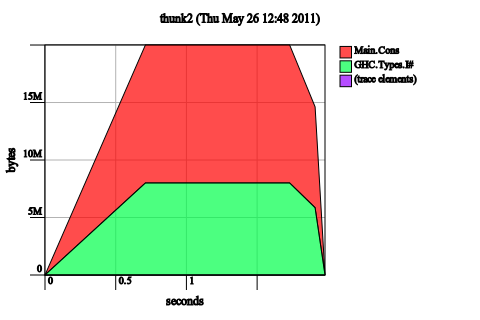
The remaining space usage is merely the strict data structure sitting in memory. In order to make this fix, that we had to go in and fiddle with the internal representation of our SpineStrictList in order to induce this strictness. Here is the answer to question one: we can’t fix this space leak by modifying the combining function, because the extra strictness we require needs to be “attached” (using a seq) to the outer constructor of the data structure itself: something you can only access if you’re able to manipulate the internal structure of the data structure.

One upshot of this is that it’s quite annoying when your favorite container library fails to provide a strict version of a function you need. In fact, historically this has been a problem with the containers package, though I’ve recently submitted a proposal to help fix this.

Make the structure value strict. This is a “nicer” way of turning ssMap into its strict version, since the bang patterns will do all the seq work for you:

data StrictList a = Nil | Cons !a !(SpineStrictList a)

Of course, if you actually want a spine strict but value lazy list, this isn’t the best of worlds. However, in terms of flexibility, a fully strict data structure actually is a bit more flexible. This is because you can always simulate the value lazy version by adding an extra indirection:

data Lazy a = Lazy a
type SpineStrictList a = StrictList (Lazy a)

Now the constructor Lazy gets forced, but not necessarily its insides. You can’t pull off this trick with a lazy data structure, since you need cooperation from all of the functions to get the inside of the container evaluated at all. There is one downside to this approach, however, which is that the extra wrapper does have a cost in terms of memory and pointer indirections.

Make the structure lazy. Fascinatingly enough, if we add laziness the space leak goes away:

data SpineStrictList a = Nil | Cons a (SpineStrictList a)

instance NFData a => NFData (SpineStrictList a) where
    rnf Nil = ()
    rnf (Cons x xs) = rnf x `seq` rnf xs

main = do
    let l = ssFromListL ([1..1000000] :: [Int])
        f x = ssMapL permute x
    evaluate (rnf (f (f (f (f (f (f (f (f l)))))))))

ssFromListL [] = Nil
ssFromListL (x:xs) = Cons x (ssFromListL xs)
ssMapL _ Nil = Nil
ssMapL f (Cons x xs) = Cons (f x) (ssMapL f xs)

We’ve added an rnf to make sure that everything does, in fact, get evaluated. In fact, the space usage dramatically improves!

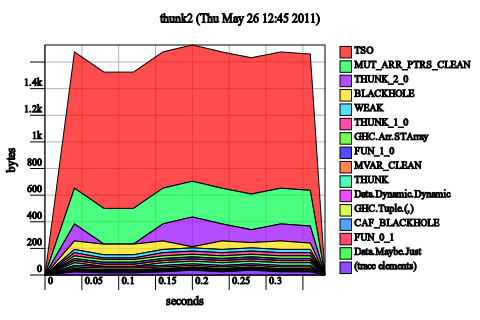
What happened? The trick is that because the data structure was lazy, we didn’t actually bother creating 1000000 thunks at once; instead, we only had thunks representing the head and the tail of the list at any given time. Two is much smaller than a million, and the memory usage is correspondingly smaller. Furthermore, because rnf doesn’t need to hold on to elements of the list after it has evaluated them, we manage to GC them immediately afterwards.

Fusion. If you remove our list-like data constructor wrapper and use the built-in list data type, you will discover that GHC is able to fuse-away all of the maps into one, extremely fast, unboxed operation:

main = do
    let l = [1..1000000] :: [Int]
        f x = map permute x
    evaluate (rnf (f (f (f (f (f (f (f (f l)))))))))

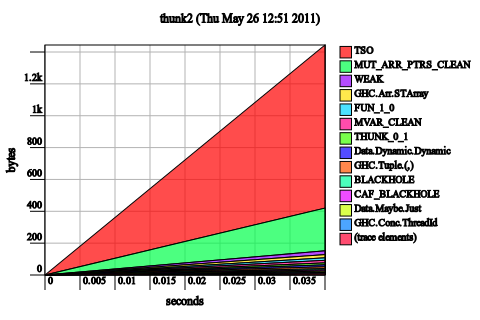
This is not completely fair: we could have managed the same trick with our strict code; however, we cannot use simple foldr/build fusion, which does not work for foldl (recursion with an accumulating parameter.) Nor can we convert our functions to foldr without risking stack overflows on large inputs (though this may be acceptable in tree-like data structures which can impose a logarithmic bound on the size of their spine.) It’s also not clear to me if fusion derives any benefit from spine strictness, though it definitely can do better in the presence of value strictness.

Commentary

In this post, we discussed how to fix the common accumulation of thunks inside spine-strict data structures. What we found was that if the structure was lazy in its structure, the rampant accumulation of thunks is avoided since not all of the leafs have thunks applied to them, and we found that if the structure was strict in its values, the thunks could also be avoided. We also discovered that, for a spine-strict value-lazy structure, the library itself must provide value-strict versions of all of their functions: these functions cannot be easily implemented by the user.

The conclusion I draw from all of these facts is that the spine-strict, value-lazy data structure is a very specialized beast that should only be used in very rare situations. It can be perhaps used to implement a memotable or dynamic programming, but in the event of updates and other “modification” functions, such a structure will almost never do what an ordinary user expects it to do. It should be noted that this does not mean that laziness is the problem: as we saw, many modifications to structures can be streamed, resulting in much better space usage. This is a point we will return to when we discuss streaming leaks. However, it is unclear if we can profitably convert existing spine-strict data structures into spine-lazy ones without paying large indirection costs. That is a topic of ongoing research.

If it has lots of comments, it's probably buggy

Yesterday we had guest speaker Byron Cook come in to give a talk about SLAM, a nice real-world example of theorem proving technology being applied to device drivers.

Having worked in the trenches, Byron had some very hilarious (and interesting) quips about device driver development. After all, when a device driver crashes, it’s not the device driver writer that gets blamed: it’s Microsoft. He pointed out that, in a hardware company, “If you’re not so smart, you get assigned to write software drivers. The smart people go work on hardware”, and that when you’re reading device driver code, “If there are a lot of comments and they’re misspelled, there’s probably a bug.” Zing! We’re always used to extolling the benefits of commenting your code, but it certainly is indisputable that writing comments can help clarify confusing code to yourself, whereas if the code wasn’t confusing in the first place you wouldn’t have felt the need to write comments anyway. Thus, one situation is some guru from the days of yore wrote very clever code, and then you came along and weren’t quite clever enough to fully understand what was going on, so you wrote lots of comments to explain the code to yourself as you went along. Well, it’s not the comment’s fault, but the fact that the code was too clever for you probably means you introduced a bug when you made your modifications.

The approach used by SLAM to deal with the exponential state space explosion was also pretty interesting. What they do is throw out as much state as possible (without eliminating the bug), and then see whether or this simplified program triggers a bug. It usually does, though due to a spurious transition, so then they introduce just enough extra state to remove that spurious path, and repeat until the simplified program is judged to fulfill the assert (success) or we come across a path in the simplified program which is not spurious in the real program. The other really interesting bit was their choice of specification language was essentially glorified asserts. In an academic class like Temporal Logic, you spend most of your time studying logics like CTL and LTL, which are strange and foreign to device driver writers; asserts are much easier to get people started with. I could definitely see this applying to other areas of formal verification as well (assert based type annotations, anyone?)

Postscript. I have some absolutely gargantuan posts coming down the pipeline, but in between revising for exams and last minute review sessions, I haven’t been able to convince myself that finishing up these posts prior to exams is a good use of my time. But they will come eventually! Soon! I hope!

Tail recursion makes your loops cleaner

Recursion is one of those things that functional programming languages shine at—but it seems a bit disappointing that in many cases, you have to convert your beautiful recursive function back into iterative form. After all, iteration is what imperative languages do best, right?

Actually, explicitly tail-recursive functions in functional programming languages can be fairly beautiful: in fact, in the cases of complicated loops, they can be even prettier than their imperative counterparts. Take this midpoint line-drawing algorithm as an example:

circleMidpoint d r = go 0 (-r) k0
    where k0 = 5 - 4 * r
          x1 = ceiling (fromIntegral r / sqrt 2)
          go x y k | x > x1    = return ()
                   | k > 0     = d (x,y) >> go (x+1) (y+1) (k+8*x+8*y+20)
                   | otherwise = d (x,y) >> go (x+1)  y    (k+8*x+12)

There are three loop variables: x, y and k, and depending on various conditions, some of them get updated in different ways. x is a bog-standard loop variable; ye old C-style for loop could handle it just fine. But y and k are updated differently depending on some loop conditions. But since they’re parameters to the go helper function, it’s always clear what the frequently changing variables are. You lose that nice structure in the imperative translation:

// global variables and loop variables are all mixed together
int k = 5 - 4 * r;
int y = -r;
int x1 = ceil(r/sqrt(2));
for (int x = 0; x <= x1; x++) { // only x is obviously an index var
  draw(x, y);
  if (k > 0) {
    y++;
    k += 8*x + 8*y + 20;
  } else {
    k += 8*x + 12;
  }
  // does it ever make sense for any code to live here?
}

I’ve also managed to introduce a bug in the process…

Computing function composition

This is an addendum to my second example in Anatomy of a thunk leak, in which I’d like to propose another solution to the space leak, involving computing the composition of all of these thunks. This solution is particularly notable because it preserves the denotation of the original function, that is, that f l (undefined, undefined) = (undefined, undefined). This should be surprising, because I claimed that it would be impossible for GHC to optimize a function with that had this denotation into one without the space leak by more eagerly evaluating some thunks. There is no contradiction: the optimization we would like to apply here is one of partial evaluation. Didn’t understand that? Don’t worry, a concrete example is coming soon.

As Heinrich Apfelmus points out, the space leak can be visualized as a large graph of expressions which has not been collapsed into a single value: 1 + (1 + (1 + (1 + (1 + (1 + ...))))). We can visualize this graph being built up in successive iterations of the function:

The point of introducing strictness (and thus changing the denotation of the function) is that we keep collapsing (evaluating) the tree.

But notice the value highlighted in red: we must know what this value is before we can do any computation. But if this value is unknown (or, in our case, if we don’t want to evaluate it while we are forming this graph), our strategy doesn’t really work. We can’t collapse the entire tree. However, (and this is the key), because addition is associative, we can rotate the tree, and then evaluate the (now left) subtree.

In effect, all of the thunks have been merged together: instead of 1 + 1 + 1 + X. we now have 3 + X. Simple! Here is the implementation:

f l (x0, x1) = go l (0, 0)
    where go [] (!c0, !c1) = (c0 + x0, c1 + x1)
          go (x:xs) !c     = go xs (tick x c)

tick x (!c0, !c1) | even x    = (c0, c1 + 1)
                  | otherwise = (c0 + 1, c1)

go is essentially the strict version of f, but at the end of the iteration it returns a pair with two thunks: c0 + x0 and c1 + x1, were both c0 and c1 have been fully evaluated.

Here’s another way of thinking of how we’re doing things:

It would be pretty cool if this could be done automatically, and it would pretty applicable in other domains too. Combining functions that are associative are a precious commodity when it comes to parallelization.

Anatomy of a thunk leak

In this post, we discuss the characteristics of a thunk leak, the leak that has come to symbolize the difficulties of “reasoning about space usage” in Haskell. I’ll consider a few examples of this type of leak and argue that these leaks are actually trivial to fix. Rather, the difficulty is when a thunk leak gets confused with other types of leaks (which we will cover in later posts).

Description

I’ll be describing the various leaks in two ways: I will first give an informal, concrete description using the metaphor I developed in the Haskell Heap series, and then I will give a more direct, clinical treatment at the end. If you can’t stand one form of explanation or the other, feel free to skip around.

Thunk leaks occur when too many wrapped presents (thunks) are lying around at the same time.

The creation of thunks is not necessarily a bad thing: indeed, most Haskell programs generate lots of thunks. Sometimes the presence of thunks on the heap is unavoidable. The problem is when they do not get evaluated in due course: like socks in the room of a lazy college student, they start piling up.

There is a precise sense by which the thunks “pile” up, which can be observed by looking at the presents the ghosts care about.

Each ghost cares about the next present in the pile (so the Grinch can’t steal them away), and we (the user) care about the present at the very bottom of the pile. Thus, when we open that present, the whole chain of presents comes toppling down (assuming there are not other references pointed to the pile).

The chain of thunks could really be any shape you want, though linear is the usual case.

What would fixing the problem look like? It’s certainly not waiting until the presents get piled up and then cleaning them up in one go (as our college student might do): the damage (big memory usage) has already been done!

Rather, we should be a bit more eager and open up our presents as we get them.

This strategy can fail, however. If opening the presents results in something even bigger than we started off with or if we might not need to open all the presents, we might be better off just being lazy about it.

There’s also the question of where all these presents came from in the first place. Maybe we were too eager about getting the presents in the first place…

In summary, a thunk leak is when a Haskell program builds up a large number of thunks that, if evaluated, would result in much smaller memory usage. This requires such thunks to have several properties:

1. They must not have external references to them (since the idea is as the thunks are evaluated, their results can get garbage collected),
2. They must perform some sort of reduction, rather than create a bigger data structure, and
3. They should be necessary.

If (1) fails, it is much more probable that these thunks are legitimate and only incur a small overhead (and the real difficulty is an algorithmic one). If (2) fails, evaluating all of the thunks can exacerbate the memory situation. And if (3) fails, you might be looking at a failure of streaming, since thunks are being eagerly created but lazily evaluated (they should be lazily created as well).

Diagnosis

As with most space leaks, they usually only get investigated when someone notices that memory usage is unusually high. However, thunk leaks also tend to result in stack overflows when these thunk chains get reduced (though not always: a thunk chain could be tail recursive.) As with all performance tuning, you should only tune while you are doing measurements: otherwise, you may spend a lot of time optimizing something that is relatively insignificant (or worse yet, that GHC already optimized for you!)

The next line of diagnosis is the heap residency profile, which does not require you to recompile your program with profiling enabled. Just add -hT as an RTS flag. In the case of thunk leak, the heap profile is very tell-tale: a large chunk of the heap will be occupied with THUNK. Bingo!

Note. This diagnostic step is why I’ve chosen to distinguish between thunk leaks and live variable leaks. A thunk leak will have thunks dominating the heap because the thunks themselves are numerous and are consuming memory. A live variable leak may be caused by a thunk retaining extra memory, but the thunks themselves may not necessarily show up on the heap, because you only need one reachable thunk to cause memory to be retained.

Examples

I’ve distilled some examples in order to help illustrate the phenomenon in question, as well as give direct, source-level indications on all the possible ways you can go about fixing the leak. I’ll also give some examples of things that could have leaked, but didn’t because GHC was sufficiently clever (hooray for optimizations!) Runnable code can be found in the GitHub repository, which I will try to keep up-to-date.

We’ll first start with the classic space leak from naive iterative code:

main = evaluate (f [1..4000000] (0 :: Int))

f []     c = c
f (x:xs) c = f xs (c + 1)

It should be obvious who is accumulating the thunks: it’s c + 1. What is less obvious, is that this code does not leak when you compile GHC with optimizations. Why is this the case? A quick look at the Core will tell us why:

Main.$wf =
  \ (w_s1OX :: [GHC.Integer.Type.Integer])
    (ww_s1P0 :: GHC.Prim.Int#) ->
    case w_s1OX of _ {
      [] -> ww_s1P0;
      : _ xs_a1MR -> Main.$wf xs_a1MR (GHC.Prim.+# ww_s1P0 1)
    }

Notice that the type of c (renamed to ww_s1P0) is GHC.Prim.Int#, rather than Int. As this is a primitive type, it is unlifted: it is impossible to create thunks of this type. So GHC manages to avoid thunks by not creating them at all in the first place. Fixing the unoptimized case is as simple as making c strict, since addition of integers is a strict function.

It is not, in general, possible for GHC to do this kind of unboxing optimization without violating the semantics of our code. Our next piece of code looks at precisely such a case:

main = do
    evaluate (f [1..4000000] (0 :: Int, 1 :: Int))

f []     c = c
f (x:xs) c = f xs (tick x c)

tick x (c0, c1) | even x    = (c0, c1 + 1)
                | otherwise = (c0 + 1, c1)

This space leaks both with and without optimizations. It also stack overflows.

It is not possible for GHC to optimize this code in such a way that the elements of the pair are eagerly evaluated without changing the semantics of the function f. Why is this the case? We consider an alternate call to f: f [1..4000000] (0, undefined). The current semantics of the function demand that the result be (2000000, undefined) (since anything added to undefined is undefined), which means we cannot do any evaluation until the inside of the resulting tuple is forced. If we only ever evaluate the tuple to whnf (as the call to evaluate does) or if we only ever use the first result, then no exception should be thrown. This is indeed the case if we replace 1 :: Int with undefined and run the program.

OK, that’s enough theory, how do we fix this bug? I could just give you a single answer, but I think it will be more informative if we consider a range of possible fixes and analyze their effect on the program. Hopefully, this will make space leaks less like casting the runes, and much more methodical.

Add a bang-pattern to c in f. This doesn’t work:

f []     !c = c
f (x:xs) !c = f xs (tick x c)

The insight is that we’ve not changed the semantics of the function at all: f l (undefined, undefined) still should result in (undefined, undefined), since seq doesn’t “look inside the tuple”. However, adding this bang-pattern may help in the construction of other solutions, if evaluating the tuple itself has other side-effects (as we might say, that ghost might open some presents for us).

Make the tuple in tick irrefutable. This is just confused:

tick x ~(c0, c1) | even x    = (c0, c1 + 1)
                 | otherwise = (c0 + 1, c1)

Irrefutable patterns add laziness, not strictness, so it’s not surprising that the problem has gotten worse (note the memory usage is now up to 80M, rather than 40M).

Make tick strict. Notice that the x is already forced immediately by even x, so there’s no need to add a bang pattern there. So we just add bang patterns to c0 and c1:

tick x (!c0, !c1) | even x    = (c0, c1 + 1)
                  | otherwise = (c0 + 1, c1)

These might look like a terrible graph, but look at the scale. 1.2 kilobytes. In general, if after you make a change to a Haskell program and you start seeing lots of bands again, it means you’ve fixed the leak. So we’ve fixed it!

Well, not quite. The unoptimized code still has a leak:

We fixed our space leak by enabling a GHC optimization, similar to the one that fixed our original space leak. Once again, the Core makes this clear:

Main.$wf :: [GHC.Integer.Type.Integer]
            -> GHC.Types.Int
            -> GHC.Types.Int
            -> (# GHC.Types.Int, GHC.Types.Int #)

GHC has optimized the tuple away into an unboxed return and inlined the call to tick, as a result we don’t have any tuple thunks floating around. We could have manually performed this optimization, but it’s better to the let the compiler do it for us (and keep our code clean.)

Strictify tick and f. In analogy with the first example, now that tick is strict, if we strictify both places, the unoptimized code will also be fine. And indeed, it is.

It doesn’t help us much for the optimized case though! (There is essentially no change to the heap profile.)

Make the pair strict. Using a strict pair instead of the default lazy pair is equivalent to inserting bang patterns every where we pattern match on a tuple. It is thus equivalent to strictifying tick, and if you do this you will still need a little extra to get it working in the unoptimized case. This tends to work better when you control the data structure that is going into the loop, since you don’t need to change all of your data declarations.

Deep seq c. If a simple bang pattern for c doesn’t work, a deep bang pattern will:

f []     c = c
f (x:xs) c@(!_,!_) = f xs (tick x c)

Alternatively, you could have used rnf from the deep seq package. While this does work, I personally think that it’s better policy to just use a strict data type, if you’re going to be rnf’ing willy-nilly, you might as well keep things fully evaluated all the time.

I had another example, but I’m out of time for today! As some parting words, note that tuples aren’t the only lifted types floating around: everything from records to single data constructors (data I a = I a) to mutable references have these extra semantics which can have extra space costs. But identifying and fixing this particular problem is really easy: the heap profile is distinctive, the fix is easy and non-invasive, and you even have denotational semantics to aid your analysis of the code! All you need is a little extra knowledge.

Postscript. Apologies for the wildly varying graph axes and shifty colors. Try to focus on the shape and labeling. I’m still wrangling hp2pretty to get it to generate the right kinds of heap profiles, and I need a more consistent scaling mechanism and more consistent coloring. Experiments were done on GHC 6.12.3.

Space leak zoo

A big thanks to everyone who everyone who sent in space leak specimens. All of the leaks have been inspected and cataloged by our experts, and we are quite pleased to open the doors of the space leak zoo to the public!

There are a few different types of space leak here, but they are quite different and a visitor would do well not to confuse them (the methods for handling them if encountered in the wild vary, and using the wrong technique could exacerbate the situation).

• A memory leak is when a program is unable to release memory back to the operating system. It’s a rare beast, since it has been mostly eliminated by modern garbage collection. We won’t see any examples of it in this series, though it is strictly possible for Haskell programs to exhibit this type of leak if they use non-bracketed low-level FFI allocation functions.
• A strong reference leak is when a program keeps around a reference to memory that in principle could be used but actually will never be used anymore. A confluence of purity and laziness make these types of leaks uncommon in idiomatic Haskell programs. Purity sidesteps these leaks by discouraging the use of mutable references, which can leak memory if they are not cleared when appropriate. Laziness sidesteps these leaks by making it difficult to accidentally generate too much of a data structure when you only want parts of it: we just use less memory to begin with. Of course, using mutable references or strictness in Haskell can reintroduce these errors (sometimes you can fix instances of the former with weak references—thus the name, “strong reference” leak), and live variable leaks (described below) are a type of strong reference leak that catch people unfamiliar with closures by surprise.
• A thunk leak is when a program builds up a lot of unevaluated thunks in memory which intrinsically take up a lot of space. It can be observed when a heap profile shows a large number of THUNK objects, or when you stack overflow from evaluating a chain of these thunks. These leaks thrive on lazy evaluation, and as such are relatively rare in the imperative world. You can fix them by introducing appropriate strictness.
• A live variable leak is when some closure (either a thunk or a lambda) contains a reference to memory that a programmer expects to have been freed already. They arise because references to memory in thunks and functions tend to be implicit (via live variables) as opposed to explicit (as is the case for a data record.) In instances where the result of the function is substantially smaller, these leaks can be fixed by introducing strictness. However, these are not as easy to fix as thunk leaks, as you must ensure all of the references are dropped. Furthermore, the presence of a large chunk of evaluated memory may not necessarily indicate a live variable leak; rather, it may mean that streaming has failed. See below.
• A streaming leak is when a program should only need a small amount of the input to produce a small amount of output, thus using only a small amount of memory, but it doesn’t. Instead, large amounts of the input are forced and kept in memory. These leaks thrive on laziness and intermediate data structures, but, unlike the case of thunk leaks, introducing strictness can exacerbate the situation. You can fix them by duplicating work and carefully tracking data dependencies.
• A stack overflow is when a program builds up a lot of pending operations that need to performed after the current execution. It can be observed when your program runs out of stack space. It is, strictly speaking, not a space leak, but an improper fix to a thunk leak or a streaming leak can convert it into a stack overflow, so we include it here. (We also emphasize these are not the same as thunk leaks, although sometimes they look the same.) These leaks thrive on recursion. You can fix them by converting recursive code to iterative style, which can be tail-call optimized, or using a better data structure. Turning on optimization also tends to help.
• A selector leak is a sub-species of a thunk leak when a thunk that only uses a subset of a record, but because it hasn’t been evaluated it causes the entire record to be retained. These have mostly been killed off by the treatment of GHC’s selector thunks by the RTS, but they also occasionally show due to optimizations. (See below.)
• An optimization induced leak is a camouflaged version of any of the leaks here, where the source code claims there is no leak, but an optimization by the compiler introduces the space leak. These are very tricky to identify; we would not put these in a petting zoo! (You can fix them by posting a bug to GHC Trac.)
• A thread leak is when too many Haskell threads are lying around. You can identify this by a contingent of TSO on the heap profile: TSO stands for thread-state object. These are interesting to debug, because there are a variety of reasons why a thread may not dying.

In the next post, we’ll draw some pictures and give examples of each of these leaks. As an exercise, I invite interested readers to categorize the leaks we saw last time.

Update. I’ve separated thunk leaks from what I will now call “live variable leaks,” and re-clarified some other points, especially with respect to strong references. I’ll expand on what I think is the crucial conceptual difference between them in later posts.

Reified laziness

Short post, longer ones in progress.

One of the really neat things about the Par monad is how it explicitly reifies laziness, using a little structure called an IVar (also known in the literature as I-structures). An IVar is a little bit like an MVar, except that once you’ve put a value in one, you can never take it out again (and you’re not allowed to put another value in.) In fact, this precisely corresponds to lazy evaluation.

The key difference is that an IVar splits up the naming of a lazy variable (the creation of the IVar), and specification of whatever code will produce the result of the variable (the put operation on an IVar). Any get to an empty IVar will block, much the same way a second attempt to evaluate a thunk that is being evaluated will block (a process called blackholing), and will be fulfilled once the “lazy computation” completes (when the put occurs.)

It is interesting to note that this construction was adopted precisely because laziness was making it really, really hard to reason about parallelism. It also provides some guidance for languages who might want to provide laziness as a built-in construct (hint: implementing it as a memoized thunk might not be the best idea!)