June 27, 2011Today I would like to describe how I pin down compiler bugs, specifically, bugs tickled by optimizations, using a neat feature that Hoopl has called optimization fuel. Unfortunately, this isn’t a particularly Googleable term, so hopefully this post will get some Google juice too. Optimization fuel was originally introduced by David Whalley in 1994 in a paper Automatic isolation of compiler errors. The basic idea is that all optimizations performed by the compiler can be limited (e.g. by limiting the fuel), so when we suspect the optimizer is misbehaving, we binary search to find the maximum amount of fuel we can give the compiler before it introduces the bug. We can then inspect the offending optimization and fix the bug. Optimization fuel is a feature of the new code generator, and is only available if you pass -fuse-new-codegen to GHC.
The bug
The bug shows up when I attempt to build GHC itself with the new code generator. Building GHC is a great way to ferret out bugs, since it has so much code in it, it manages to cover a lot of cases:
"inplace/bin/ghc-stage1" (...) -o compiler/stage2/build/FastString.o
ghc-stage1: panic! (the 'impossible' happened)
(GHC version 7.1 for i386-unknown-linux):
RegAllocLinear.makeRegMovementGraph
Please report this as a GHC bug: http://www.haskell.org/ghc/reportabug
We quickly grep the codebase to find the relevant error, which is in compiler/nativeGen/RegAlloc/Linear/JoinToTargets.hs:
-- | Construct a graph of register\/spill movements.
--
-- Cyclic components seem to occur only very rarely.
--
-- We cut some corners by not handling memory-to-memory moves.
-- This shouldn't happen because every temporary gets its own stack slot.
--
makeRegMovementGraph :: RegMap Loc -> RegMap Loc -> [(Unique, Loc, [Loc])]
makeRegMovementGraph adjusted_assig dest_assig
= let
mkNodes src vreg
= expandNode vreg src
$ lookupWithDefaultUFM_Directly
dest_assig
(panic "RegAllocLinear.makeRegMovementGraph")
vreg
in [ node | (vreg, src) <- ufmToList adjusted_assig
, node <- mkNodes src vreg ]
But the source code doesn’t particularly suggest what the problem might be. Time to start using optimization fuel!
Binary search
We can modify the amount of optimization fuel GHC has, for running optimizations, by changing the value of -dopt-fuel. The first thing we do if see the bug is present with zero optimization fuel:
$ "inplace/bin/ghc-stage1" (...) -o compiler/stage2/build/FastString.o -dopt-fuel=0
Great, it worked! We pick some large number to start our binary search at (and pass -fforce-recomp, so GHC actually compiles the program.)
$ "inplace/bin/ghc-stage1" (...) -o compiler/stage2/build/FastString.o -dopt-fuel=1000 -fforce-recomp
ghc-stage1: panic! (the 'impossible' happened)
(GHC version 7.1 for i386-unknown-linux):
RegAllocLinear.makeRegMovementGraph
Please report this as a GHC bug: http://www.haskell.org/ghc/reportabug
I then binary search (test 500, if that fails test 750, etc), until I find the point at which adding one to the fuel causes the failure.
$ "inplace/bin/ghc-stage1" (...) -o compiler/stage2/build/FastString.o -dopt-fuel=709 -fforce-recomp
$ "inplace/bin/ghc-stage1" (...) -o compiler/stage2/build/FastString.o -dopt-fuel=710 -fforce-recomp
ghc-stage1: panic! (the 'impossible' happened)
(GHC version 7.1 for i386-unknown-linux):
RegAllocLinear.makeRegMovementGraph
Viewing the culprit
How do we convince GHC to tell us what optimization it did with the 710st bit of fuel? My favorite method is to dump out the optimized C– from both runs, and then do a diff. We can dump the C– to a file using -ddump-opt-cmm -ddump-to-file, and then diff reveals:
@@ -10059,7 +10059,6 @@
}
c45T:
_s3es::I32 = I32[Sp + 4];
- _s3eu::I32 = I32[Sp + 0];
// deleted: if (0) goto c460;
// outOfLine should follow:
_s3er::I32 = 0;
@@ -10093,1354 +10092,3 @@
jump (I32[Sp + 0]) ();
}
The optimization is deleting an assignment. Is this valid? Here is the full code, with some annotations:
FastString.$whashStr_entry()
{ [const 131081;, const 0;, const 15;]
}
c45T:
_s3es::I32 = I32[Sp + 4];
_s3eu::I32 = I32[Sp + 0]; // deleted assignment
_s3er::I32 = 0;
_s3ex::I32 = 0;
goto c463;
c460:
R1 = FastString.$whashStr_closure;
jump (I32[BaseReg - 4]) ();
c463:
if (I32[GHC.Types.Bool_closure_tbl + ((_s3er::I32 == _s3es::I32) << 2)] & 3 >= 2) goto c46d;
// uh oh, assignment used here
_s3IC::I32 = %MO_S_Rem_W32(%MO_UU_Conv_W8_W32(I8[_s3eu::I32 + (_s3er::I32 << 0)]) + _s3ex::I32 * 128,
4091);
_s3er::I32 = _s3er::I32 + 1;
_s3ex::I32 = _s3IC::I32;
goto c463;
c46d:
R1 = _s3ex::I32;
Sp = Sp + 8;
jump (I32[Sp + 0]) ();
}
Seems not: the variable is used in MO_S_Rem_W32: that’s no good. We conclude that the bug is in an optimization pass, and it is not the case that the register allocator failed to handle a case that our optimization is now tickling.
Fixing the bug
With this information, we can also extract the program fragment that caused this bug:
hashStr :: Ptr Word8 -> Int -> Int
hashStr (Ptr a#) (I# len#) = loop 0# 0#
where
loop h n | n GHC.Exts.==# len# = I# h
| otherwise = loop h2 (n GHC.Exts.+# 1#)
where !c = ord# (indexCharOffAddr# a# n)
!h2 = (c GHC.Exts.+# (h GHC.Exts.*# 128#)) `remInt#` 4091#
We can also see how our pipeline is processing the program, and observe precisely where in the process the bad optimization was made:
==================== Post Proc Points Added ====================
{offset
c43r:
_s3es::I32 = I32[(old + 8)];
_s3eu::I32 = I32[(old + 12)];
if (Sp - <highSp> < SpLim) goto c43y; else goto c43u;
==================== Post spills and reloads ====================
{offset
c43r:
_s3es::I32 = I32[(old + 8)];
_s3eu::I32 = I32[(old + 12)];
if (Sp - <highSp> < SpLim) goto c43y; else goto c43u;
==================== Post rewrite assignments ====================
{offset
c43r:
_s3es::I32 = I32[(old + 8)];
if (Sp - <highSp> < SpLim) goto c43y; else goto c43u;
Since this is a spurious instance of code removal, we look for all mentions of emptyGraph in the rewrite assignments optimization pass:
usageRewrite :: BwdRewrite FuelUniqSM (WithRegUsage CmmNode) UsageMap
usageRewrite = mkBRewrite3 first middle last
where first _ _ = return Nothing
middle :: Monad m => WithRegUsage CmmNode O O -> UsageMap -> m (Maybe (Graph (WithRegUsage CmmNode) O O))
middle (Plain (CmmAssign (CmmLocal l) e)) f
= return . Just
$ case lookupUFM f l of
Nothing -> emptyGraph
Just usage -> mkMiddle (AssignLocal l e usage)
middle _ _ = return Nothing
last _ _ = return Nothing
This looks like it should be an unobjectionable case of dead assignment elimination coupled with liveness analysis, but for some reason, the backwards facts are not being propagated properly. In fact, the problem is that I attempted to optimize the Hoopl dataflow function, and got it wrong. (Fixpoint analysis is tricky!) After reverting my changes, the unsound optimization goes away. Phew.
June 24, 2011This post describes how to change which monitor xmobar shows up on in a multi-monitor setup. This had always been an annoyance for me, since on an initial switch to multi-monitor, xmobar would be living on the correct monitor, but if I ever restarted XMonad thereafter, it would migrate to my other monitor, much to my annoyance. Note that a monitor is different from an X screen, which can be directly configured from xmobar using the -x command line.
How does xmobar pick what screen to use? It selects the “primary” monitor, which by default is the first entry in your xrandr list:
Screen 0: minimum 320 x 200, current 2464 x 900, maximum 8192 x 8192
VGA1 connected 1440x900+1024+0 (normal left inverted right x axis y axis) 408mm x 255mm
1440x900 59.9*+ 75.0
1280x1024 75.0 60.0
1280x960 60.0
1152x864 75.0
1024x768 75.1 70.1 66.0 60.0
832x624 74.6
800x600 72.2 75.0 60.3 56.2
640x480 72.8 75.0 66.7 66.0 60.0
720x400 70.1
LVDS1 connected 1024x768+0+0 (normal left inverted right x axis y axis) 245mm x 184mm
1024x768 60.0*+
800x600 60.3 56.2
640x480 59.9
We can switch the primary monitor using the xrandr --output $MONITOR --primary command. However, this change is not persistent; you’d have to run this command every time you add a new monitor.
Fortunately, it turns out gnome-settings-daemon records information about monitors it has seen in order to configure them properly. This information is in .config/monitors.xml:
<monitors version="1">
<configuration>
<clone>no</clone>
<output name="VGA1">
<vendor>HSD</vendor>
<product>0x8991</product>
<serial>0x01010101</serial>
<width>1440</width>
<height>900</height>
<rate>60</rate>
<x>0</x>
<y>0</y>
<rotation>normal</rotation>
<reflect_x>no</reflect_x>
<reflect_y>no</reflect_y>
<primary>no</primary>
</output>
<output name="LVDS1">
<vendor>LEN</vendor>
<product>0x4002</product>
<serial>0x00000000</serial>
<width>1024</width>
<height>768</height>
<rate>60</rate>
<x>1440</x>
<y>0</y>
<rotation>normal</rotation>
<reflect_x>no</reflect_x>
<reflect_y>no</reflect_y>
<primary>no</primary>
</output>
</configuration>
</monitors>
So all we need to do is tweak primary to be yes on the appropriate monitor.
Hat tip to David Benjamin and Evan Broder for letting me know how to do this.
June 22, 2011This is notebook two.
Max Schäfer: Refactoring Java
Most Java refactoring tools built into IDEs like Eclipse are little more than glorified text manipulation macros. There are no guarantees that the result of your refactoring will have the same behavior as the original: you can even refactor code that doesn’t even compile! To prevent this, most refactorings require heavy and hard-to-understand preconditions for refactoring. Max brings two ideas to the table:
- Rather than attempt to write a complex pre-condition that may or may not accurately reflect safety concerns, we instead do the transformation, and then verify that the refactoring did not break anything. We can do this with a dependency-based description of the behavior program, which overspecifies the original semantics (otherwise, such analysis wouldn’t be tractable, as it’s undecidable.)
- Rather than attempt to write a monster refactoring that attempts to handle all possible cases, we decompose refactorings into microrefactorings on simpler versions of the source language. For example, moving a chunk of code into a method would involve closure conversion (control), lambda lifting (data), and then the actual outwards motion, which at this point is trivial. We can then resugar into the original source language. This allows us to abstract over corner cases.
Modularity is a very powerful philosophy, and one that Hoopl takes too. (One might wonder if Hoopl might be useful for refactoring, one big problem I observe is that Hoopl’s representation is too low level, and really the point of a high-level language is that you don’t need complex dataflow analysis.)
There are some bad assumptions about this, however. It assumes we know the whole program, that it’s only written in one language (no XML manifest files), and it’s statically typed and class based. Of course, one fails these assumptions for all real programs, so if we actually want people to adopt this workflow, we need a story for them. Refactoring is a transition from sloppy to structured code. (I have scribbled at the bottom of the page responsibility calculus, but I have no idea what that means now.)
Semantic overspecification reminds me of SLAM’s approach to iterative approximations of program behavior.
Mike Dodds: Modular Reasoning for Deterministic Parallelism
A frequent problem with separation logics is that you need to introduce a new primitive for every sort of concurrency construct you may want to model, and so you end up with a bazillion different logics, each for your own model of concurrency. Mike presents a way of incrementally building up any sort of semantics you could possibly want, using “concurrent abstract predicates.” You use predicates to generate variables that satisfy various predicates, and then require these conditions for various other specifications of functions.
The majority of this particular talk was working through an odd concurrency construct called wait/grant, described in “Quasi-Static Scheduling for Safe Futures.” It’s a barrier that preserves “necessary” sequential dependencies. A bit of time was spent actually clarifying what this construct did, and why it was different from a buffered channel. Tony Hoare remarked that it resembled a “production line” in real-life, which was not very common in programming, though it happened to be quite natural for the problem the original paper authors were tackling (parallelizing sequential programs).
My notes invite me to “implement this in Haskell”, and also have a remark about “tree shaped bit vector propagation”, which is apparently the optimized version. There are also a bunch of code snippets but I’m sure I can find those in the slides.
Tomas Petricek: Joinads
Joinads for F# are a system for pattern matching on computations (as opposed to just values). How is this any different from monads? Joinads support extra operations: merge :: m a -> m b -> m (a, b) and choose :: [m (Maybe (m a))] -> m a, which can implement special scheduling properties. This can be useful for futures (Manticore), events (FRP) or the join calculus (joins execute when a channel contains value: it’s cheap and cheerful multiplexing.) It turns out you get a Joinad for free from commutative monads, which might say something about what kind of syntax extensions would be useful for those monads.
I wasn’t particularly impressed by this talk, for whatever reason. I guess my reason was I didn’t feel any deep theoretical reason why Joinads might be a particularly interesting theoretical construct to study, nor did it seem that that they were in any sense minimal. Also, in Haskell, we implement multiplexing by just forking off extra green threads, which is a much nicer model, in my opinion.
Computing with Real Numbers
Dan Piponi has written on this topic before, but this talk really helped put things in perspective for me.
There are many types of numbers for which we can easily compute with: the field of two elements (booleans), integers (well, discounting overflow), and rationals (pairs of integers). But real numbers pose some difficulties. They are the metric closure of rational numbers Q, i.e. everything that can be a limit of a Cauchy sequence of Q. This is reminiscent of a decimal expansion.
We now want to consider functions over reals. How do we know if something is computable? We might try saying it is a relation from strings of digits to strings of digits, where any finite prefix of F(p) can be uniformly computed from some finite prefix of sufficient length of p. But this is clearly insufficient for something like 0.3333, where we need to read infinitely many digits to see whether or not this is truly one third. (I remark that infinity is a bit like oracles in Turing Machine land.)
Instead, we say that a sequence of rationals q_i (with i ranging over naturals) represents a real number x if |x - q_i| < 2^-i for all i. (the base doesn’t really matter). Let p(q) = x, then f is computable if there exists an F such that p(F(prefix)) = f(p(prefix). With this definition, it turns out that addition, multiplication, division, trigonometric functions, exponentiation and logarithms are computable.
An interesting restriction of function is that of continuity, familiar from any treatment in a Calculus textbook: a function f : R -> R is continuous if for all x in the domain of f, and for all ε > 0, there exists a δ > 0 that for all y in the domain of f, |x - y| < δ implies |f(x) - f(y)| < ε. It has been proposed that every computable function is continuous: thus, computability stems from our ability to approximate things, which we can’t do for discontinuous functions (which side of the discontinuity are we on?) We can further restrict functions to C(R,R), which are the set of continuous functions which can also be approximated by infinite sequences (e.g. polynomials.)
Consider the monotone intermediate value thoerem, which states that if f is monotone, f(0) < 0and f(1) > 0, there exists some x such that f(x) = 0. Can we compute this number? Bisection doesn’t work, since determining if a number is less than or greater than another is in general incomputable. (The general intermediate value theorem is not computable, since we could get infinitely close to the origin line.) We can use trisection instead. Compute f(0.3) and f(0.7), and concurrently perform the following comparisons:
- If
f(0.3) < 0, the new range is [0.3, 1] - If
f(0.3) > 0, the new range is [0, 0.3] - If
f(0.7) < 0, the new range is [0.7, 1] - If
f(0.7) > 0, the new range is [0, 0.7]
You’ll have to do a little work to get a formal proof of correctness, but it’s easy to see why this intuitively might work: comparisons take infinite time only if the number is close to the point of comparison, but then our other comparison is guaranteed to succeed, since it is some non-infinitesimal distance away. (I have a little margin note: can we use this to do cryptography?)
It turns out there are various schools on the computability of real numbers. The perspective I have just described is the Polish School. However, the Russian School says that uncomputable points don’t exist: the code fragment is the real number. Thus, effective analysis is not classical analysis. There is a correspondence between constructive and classical mathematics. Something about Banach spaces (linear operator has to be bounded), so differentiation is not computable in general, though integration is! (This is quite different from the symbolic evaluation world.) For further reading, see Computable Analysis, Springer, 2000.
Martin Escardó: Selection Functions Everywhere
I didn’t understand this talk. I don’t understand most of Martin’s work, really. But I have a bunch of quotes:
- “I don’t know why it’s called the continuation monad; there is no control, this talk is completely out of control.”
- “I’m not going to explain what this means, but I’m going to explain how this works.”
- “[Incomprehensible statement.] Which is not too deep.”
- “And the reason is, uh, probably in the next slide.”
- “Every game is of length 2: you have the first move, and then all the others.”
- “You’ll get to use the monoidal monad structure to calculate these two people.”
Selection functions select individuals with the “highest” truth value. Max-value theorem, min-value theorem and universal-value theorem (Drinker’s paradox) are all uncomputable. Selection functions are a two stage process. K A -> A is double negation elimination, J A -> A is Peirce’s law. Bekic’s lemma gives a fixpoint. Bar recursion and do induction on p (continuous function) with p as a tree. We can calculate the optimal strategy. System T plus an equation for J-shift is strongly normalizing. We can encode the axiom of countable choice (but it’s not choice anymore!). Dependent choice: (AC classical choice, Tychonoff theory, etc. See that paper.) Why is J a monad?
Sir Roger Penrose: Twistor Theory
Penrose… doesn’t give very comprehensible talks. Well, he explained the Riemann sphere (a stereographic projection) quite well, but then things got very smooshy. Some quotes: “And that’s all you have to do in mathematics: imagine it.” “Small does not apply to distance.” “So my best way to do that is draw it like a sausage.” “I don’t think I should explain this picture.” “First I’ll confuse you more.” “It can be done in cricket, and we hope it can be done in Twistor theory too.” There was an interesting aside about Cohomology: a precise nonlocal measure about the degree of impossibility; I think I perked up when I saw the Escher picture. Not even the physicists think Twistor Theory reflects reality. It’s a mathematical plaything.
On a completely unrelated note, that night RAG blind date was going on.
Conor McBride: The Kleisli Arrows of Outrageous Fortune
“Consider the following program, which is, alas, Poor!” With a slide of code containing variables b and c: “b or not b, that is the question! … or to take arms against a c of troubles.” “The world’s most successful dependently typed language: Haskell.” Wave hello to Simon Peyton-Jones in the room.
I’ve been meaning to write a blog post about this talk, and maybe still will, although the talk is no longer as fresh in my mind. Conor describes the technical machinery necessary to simulate dependent types even when you can’t obviously push values into the types. Programs should instead be strategy trees, which cover all possible responses (even though reality will select one.) We don’t need dependent types: we can use parametrized monads to encode the pre and post conditions of Hoare logic. (Resulting in a predictable world.) These are the so called “braces of upwards mobility” (upwards mobility referring to values becoming types.) This talk made me wonder if the Strathclyde Haskell Extension would be a good platform for session types, which suffer tremendously from the lack of true dependent types. (It also made me wonder about efficient type-level computation.)
The devil is ∀ (see the horns), e.g. a universal quantifier in the wrong place (I thought maybe you could view them as skolem variables). Terms hold evidence on types. (Typical Conor to make a joke about that.) Kleisli Arrow is the Hoare Triple (think about the programmable semicolon), and with bind you don’t get to choose what state you end up in (there’s an existential.) However, we can use an alternative bind which forces the demon to give us the value: Atkey parametrized monads. We also need to make sure that our naive free monad doesn’t blow up our runtime. This is not very coherent, and cleaning up this story was what I needed to do before making a real post.
Conor’s main message was that data are witness to the proofs! “I’m in the witness protection program.” If we have some piece of data, we have discharged some proof obligations. (But I wonder, what about polymorphism?)
Have you ever wondered why the matrix multiplication trick works for Floyd-Warshall all pairs shortest paths? It’s because the relevant operations form a semiring. The traditional semiring is (N, +, *, 1, 0). For classical routing algorithms like Dijkstra and Bellman-Ford it’s (N_inf, min, +, 0, inf). All the same semiring properties hold, so we can use them interchangeably.
However, real protocols do not obey the semiring axioms (distributivity versus economics.) So we‘re not actually solving the shortest path problem (stable path problems), instead, we’re finding “best path according to neighbor choice.” This talk looks a methods for converting properties of these protocols into decision procedures for constructors (a bottom-up inference method.) If we have a particular set of axioms, we want to see if we can get a counter-example when things go a bit wonky. An example given was lexicographic pair of length and then bandwidth, which is distributive. If we modify these to be add1 minplus * add0 maxMin, the one/zero elements are in the wrong place and we lose distributivity.
It turns out that when axioms are failed, what goes wrong depends on the algorithm is run. We want protocols that work in all possible configurations.
Petri nets for concurrency
We want performance nondeterminism, so we use petrinets to encode the nondeterminism contracts, and then we push a flow through the graph to figure out what kind of performance we need. Scheduling and placement is easy to handle, because they are just modifications on the petri net. But I wasn’t so sure if this approach would work, because petri nets can get pretty bit and you may not get the performance you need to do interesting analysis.
Grant Passmore: Strategy in Computer Algebra
Automated reasoning problems are undecidable, and user-guided. Computer algebra problems are unfeasible, but the algorithms tend to be black box, secret sauce solutions (e.g. Mathematica) with all sorts of tirkcs like Groebner Bases, Quantifier Elimination, SAT for nonlinear complex arithmetic (Hilbert’s Weak Nullstellensatz) and reduction to rewriting.
Grant wants to put the choice back in computer algebra. There are many choice points: quadratic preprocessing, choice of pairs, growth of basis, forward simplification. He gives a comparison of ATP and GB. With LCF, functional parameters are key. Bag of tricks is OK, but the proof procedure is a strategy.
- What about an algorithm can be changed while preserving correctness?
- What arbitrary choices are my algorithm making?
(Margin note: can we understand fusion by understanding the mutable state it creates?)
(Untitled Software Engineering talk)
A persistent problem with formal methods is they operate in a domain of assumptions and requirements, and there is no way to tell if these assumptions or requirements are right! It’s a rather philosophical question: can we have “recognized assurance deficits”: a known unknown? These are potential sources of counter-evidence. What are the worst implications of not knowing? What claims have you made? (It would be interesting to see what elements of philosophy are relevant here.) Sometimes safety arguments are just assertions “because I say so”: there is epistemic uncertainty. The talk giver argues we should swap probabilistic integrity arguments with qualitative confidence arguments: it’s a question of safety versus confidence. We should explicitly acknowledge assurance deficits, and stop taking too much on trust.
I ask the question: is there incentive for this debate to happen? (Engineers want to look good.) Giving it to evaluators is certainly worse, since they are not in a proper position to assess the system. He didn’t have an answer, but said, “Not doing so is unacceptable.”
I somewhat amusedly note that near the end he pushed some technical software for handling this, ostensibly a product of his own research program. I remain unsure about a technical solution to this particular problem.
Approximating Markov Chains
Labeled Markov processes encode continuous state spaces, and for the longest time, we’ve noted that bisimulation works for discrete state spaces, but not continuous ones. We view the final state as a probability distribution, and we press buttons on our machine (labels) to change the distribution: each label is a stochastic kernel (a generalized binary relation.) Of course, reasoning about continuous state spaces is important: they cover things like Brownian motion, performance, probabilistic process algebras with recursion, hybrid control systems (flight management systems), as well complex discrete phenomena such as population growth and stock prices.
I didn’t understand most of the technical details, but the main point was that co-bisimulation was the correct way to do this: it is only a coincidence that bisimulation works for discrete systems. The projective limit is exactly the smallest bisimilar process. Also some material on metric spaces. This certainly seems like a field where we’re just importing well-known results from esoteric fields of mathematics.
Financial Cryptography
Unbeknown to Americans, whose financial system is still stuck on magnetic stripe readers, bank cards in Europe have moved on to EMV, in which a mini-processor is embedded in your chip, which can do true challenge-response authentication. This talk looks at how we might bootstrap a P2P transaction system that bypasses banks, using the existing EMV hardware.
How might we do this? We can use a device called the CAP, which has a small display that when given a pin gives an authentication code (two factor.) We associate transactions with CAP code, so the merchant has agreed to receive money. But you still need collaboration from the banks to do this. (This is the SDA method.) So we get rid of the bank all-together and use Diffie-Hellman (DDA). The cards are simply convenient existing infrastructure to get name authentication. There are some technical details, since we can only sign 32-bits at a time, and we usually need a bit more than that. (Margin note: “the threat model was privacy advocates.”)
The talk was short, so afterwards we had a discussion why this scheme wouldn’t actually work. My objection was that it banks would simply make it illegal to use their bank cards in this way. There was a discussion whether or not they could technically enforce this: Marcus Kuhn used passports as an example, where you can’t read passports if you don’t have Internet access, since the passport itself has an embedded monotonic clock that refuses to give information to the scanner if the scanner software is not up to date. How does the passport know what the latest version is? Its clock gets updated when it sees a new scanner.) Passport security technology is pretty interesting! They invented a block cipher over the alphabet for this purpose.
Verifying the validity of QBF
SAT is exponential, and when you add quantifiers to the mix, you get “another” exponential, but this time in the certificate. How do you verify that a universally quantified formula is in fact true? The certificate in this case is extension variables and witnesses: we provide concrete implementations for all existentially quantified variables, which can then be substituted in to give a traditional SAT problem. So once we have a certificate, what was a PSPACE problem is now “just” a NP problem.
(Technical note: We want to eliminate hypotheses in topological order (using Refl, Gen and Exists). Get the quantifiers in the right order, witnesses depend on existential variables, extension variables depend on it.)
The talk described how he hooked into the internals of Squolem to get actually get these certificates. It turned out that de Bruijn was faster than name carrying (which is different from typical QBF invalidity checking.) He even found a bug in the non-LCF style validator (due to a lack of a cyclic check.)
Applications: model checking (bounded and unbounded), PSPACE problems. (Margin note: “comparison of BDD and QBF?”)
This concludes notebook two.
June 20, 2011Over the year, I’ve accumulated three notebooks worth of miscellaneous notes and musings. Since these notebooks are falling apart, I’ve decided to transfer their contents here. Warning: they might be slightly incoherent! This is the first of three notebooks. I recommend skimming the section headers and seeing if any of them pop out.
Tony Hoare: Abstract Separation Algebra
Tony Hoare wants to leverage “the hard work [that] is already solved” by placing the formalism of separation logic (e.g. Hoare triples) into an abstract algebra. The idea is that by encoding things in pairs, not triples, we can take advantage of the numerous results in algebra. The basic idea is we take a traditional triple {p} q {r} and convert it into a ordered semigroup relation p; q <= r, where ; is a monoidal operation. In the end we end up with a separation algebra, which is a monoidal lattice with an extra star operator. The choice of axioms is all: “This is abstract algebra, so you should be willing to take these axioms without having any model in mind.” (Scribbled here: “Inception as a metaphor for mathematical multi-level thinking.”) We have a homomorphism (not isomorphism) between implementations and specifications (the right direction is simplification, the left direction is a Galois connection.) In fact, as a commenter in the audience points out, this is known as the Stone Dualities—something like how two points determine a line—with contravariant points and properties. I believe Tony’s been thinking about this topic a bit since I went to this talk at the very beginning of this year, so its likely some or all of this has been superseded by later discoveries. C’est la vie!
Satnam Singh: Multi-target parallel processing
Can we write parallel code that can execute on multiple types of hardware: e.g. vectorized operations on a traditional CPU, a GPU or an FPGA? He presents an EDSL that can be embedded in any language (well, for this particular representation, C#), with constructs like newFloatParallelArray, dx9Target.toArray1D(z) and overloaded operators. In my notes, I remark: can this representation be implemented taglessly, or do we always pay the cost of building a description of the system before we can execute it? Pushing software to hardware is especially important in the face of heterogenous processors (e.g. Metropolis). Satnam was a very engaging speaker, and many of the quotes here are attributed to him—though one quote I do have is “I hope this is not going to be quoted” (don’t worry, I haven’t quoted that sentence). Dancing is a metaphor for parallel processing (though I don’t remember what the metaphor was.) What about self-modifying hardware: we mmap the circuit description and let the hardware reprogram the FPGA!
Higher level information is crucial to optimization: thus we may want a symbolic evaluator with just in time compilation (except we can’t do that for FPGAs.) Memory access fusion is important: we want to get rid of accidental semicolons. Array -> Stream / Shift = Delay. Research idea: geometric encoding of common concurrency problems. Matrix inversion is a problem (so don’t invert the matrix, silly), local memory bounds GPU versus FPGA, and scheduling problem of energy.
Building “edit automata” with one very easy, simple idea: use strace to generate trees, and then perform regular expression on the system calls to look for viral behavior. It’s an approach similar in spirit to seLinux, which runs the program in order to determine an appropriate policy for it (and then notifies you when it does something outside of normal.) But I remark, the usefulness of an strace might not be so good in the face of poorly written Gnome applications (which touch every file and their mom); nor can you strace the kernel. What about a virus that notices when its being traced? It seems this strategy would need a lot of concrete pouring to become solid. Would an strace puppeteer be useful: that is, we get to fake responses to all syscalls a program makes? Might be kind of interesting, if hard to instrument.
Streambase
Streambase is a company that implements a visual, event stream processing language. I interviewed with them to possibly work on their compiler; while I ended up turning them down, it was a very interesting interview and I think I would have had a lot of fun working for them (though working in Java, not so much!) The interview was very fun: one question was, “Explain monads to me.” Man, I still don’t know how to do that properly. (Side note: people really, really like side effects. The programming folklore around writing performant programs that work on persistent data is very new, perhaps I’d say even more so than the folklore around lazy evaluation).
Skepticism
One of the things Alexander Bird’s book Philosophy of Science taught me was how to identify unproductive skepticism, even when it is not obvious, in things such as Hume’s problem of induction. My essay on Reliabilism was quite good; it was the only essay I managed to get a first on in my philosophy supervisions during the year. Like type theory, justification is stratified, with layers upon layers.
Simon Peyton Jones: Let Should Not Be Generalized
Programmers in Hindley-Milner type systems have long enjoyed the benefits of practical type inference: we can generally expect the most general type to be inferred, and syntactic substitution of expressions in their use-sites will always typecheck. Of course, type inference algorithms are in general EXPTIME-complete, but type theorists can’t complain too much about that, since for more powerful logics inference is usually undecidable. (BTW: dictionaries constitute runtime evidence. Good way of thinking about it.) Curiously enough, in the presence of more advanced type features, writing type signatures can actually make the type checker’s job harder, but they add local equality assumptions that need to be handled by the constraint solver. Generalized let means that all of these constraints cannot be solved until we reach the call site. Can we work around this problem by doing on the fly solving of equality constraints? The French have a paper about this, but Peyton Jones recommends carrying along a jar of aspirins if you decide to read the paper. After his talk, one of the grad students remarked that Hindley-Milner is, in many ways, an anomaly: users of Agda have an expectation of needing to specify all type signatures, except in some special cases where they can eliminate them, whereas users of Haskell have an expectation of needing to specify no type signatures, except in special cases.
Stream processing of trees
A long-standing problem with the Document Object Model is that it requires the entire document to be loaded up in memory. In cases like PHP’s documentation manual, the memory usage can be over a gigabyte large. Unfortunately, the mental model for manipulating a DOM is much more natural than that for manipulating a stream of XML tag events. Is there a way to automatically project changes to the DOM into changes on a stream? We’d like to construct an isomorphism between the two. I’m seeking a functional representation of the DOM, for manipulation (you’re still going to need mutability for a DOM-style event programming model.) “Clowns to the left of me, jokers to the right” emphasizes the difference between local and global analysis. One way you might look at traversal of a token stream is simply traversal, with a zipper to keep track of where you are. Of course, the zipper takes up memory (in effect, it forms something like a stack, which is exactly how you would convert a token stream into a tree.) So we can efficiently build the tree representation without mutation, but we still end up with a tree representation. At this point, I have written down, “Stop hitting yourself.” Indeed. Can we take advantage of domain specific knowledge, a claim that I promise not to go beyond this point? The idea of projecting DOM operations into XML stream operations, and using this as a sort of measurement for how costly something is may be profitable. Of course, now I should do a literature search.
Regular expression edit distance
Given a regular expression and a non-matching string, what is the minimum number of edits necessary to make the string match? There may be multiple answers, and the algorithm should allow you to weight different changes differently.
Frank Tip: Test Generation and Fault Localization for Web Applications
Apollo takes a hybrid approach to testing web applications, combining concrete and symbolic execution. The idea is that most web applications have diffuse, early conditionalization, with no complex state transformations or loops. So, we generate path constraints on the controller and solve them, and then generate inputs which let us exercise all of the control paths. Data is code: we want to describe the data. I must not have been paying very close attention to the presentation, because I have all sorts of other things scribbled in: “Stacks are the wrong debugging mechanism for STGs” (well, yes, because we want to know where we come from. Unfortunately, knowing where we are going isn’t very useful either) and “Can we automatically generate QuickCheck shrink implementations using execution traces?” (a sort of automated test-case minimization) and a final musing, “Haskell is not a good langauge for runtime inspection or fault localization.”
Benjamin Pierce: Types and Programming Languages
It would be very cool if someone made an interactive visualization of how type systems grow and are extended as you add new features to them, a sort of visual diff for typing rules and operational semantics.
Smoothed trending
As a blogger, my page view counts tend to be very spiky, corresponding to when my post hits a popular news site and gets picked up (to date, my Bitcoin post has had 22k views. Not bad!) But this doesn’t help me figure out long term trends for my website. Is there a way to smooth the trends so that spikes become simply “popular points” on a longer term trend?
User interfaces
I want a bible of minimal technical effort best practice user interfaces, patterns that are easy to implement and won’t confuse users too much. UI design is a bit too tweaky for my tastes. In the case of intelligent interfaces, how do we not piss off the user (e.g. Google Instant.) We have a user expectation where the computer will not guess what I want. That’s just strange.
Page 32
In big letters I have: “Prove locality theorems. No action at a distance.” Almost precisely these same words Norman Ramsey would tell me while I was working with Hoopl. I think this is a pretty powerful idea.
Separation Logic and Graphical Models
I have some mathematical definitions written down, but they’re incomplete. I don’t think I wrote anything particularly insightful. This says something about the note-taking enterprise: you should record things that you would not be able to get later, but you should also make sure you follow up with all the complete information you said you’d look up later.
Jane Street
I have two pages of scribblings from solving problems over a telephone interview. I quite enjoyed them. One was a dynamic programming question (I moffed the recurrence at first but eventually got it), the second was implementing a functional programming feature in OCaml. Actually, I wanted to write a blog post about the latter, but it’s so far been consigned to my drafts bin, awaiting a day of resurrection. Later in my notes (page 74) I have recorded the on-site interview questions, unfortunately, I can’t share them with you.
Quote
“It’s like hiring an attorney to drive you across town.” I don’t remember what the context was, though.
Mohan Ganesalingam: Language of Mathematics
I really enjoyed this talk. Mohan looks at applying NLP at a domain which is likely to be more tractable than the unrestricted human corpus: the domain of mathematical language. Why is it tractable? Math defines its lexicon in text (mathematical words must be explicitly defined), we mix symbols and natural language, and the grammar is restricted. Montague Grammars are in correspondence with Denotational Semantics. Of course, like normal language, mathematical language is heavily ambiguous. We have lexical ambiguity (“prime” can describe numbers, ideals, etc.), structural ambiguity (p is normal if p generates the splitting field of some polynomial over F_0—is F_0 referring to the generating or the polynomial?), symbolic ambiguity (d(x + y), and this is not just operator overloading because parse trees can change: take for example (A+B)=C versus λ+(M=N)), and combined symbolic and textual ambiguity. It turns out the linguistic type system of maths, which is necessary to get the correct parse trees, is not mathematical at all: integers, reals and friends are all lumped into one big category of numbers and types are not extensional (objects have different types depending on contents.) We need a dynamic type system, not a structural or nominal one, and we need to infer types while parsing.
Writing notes
From December 1st. I seem to need to write concluding paragraphs that are more concluding, and use shorter sentences. Summarize parts of my arguments, give more detail about experiments, and not to forget that a large part of historic mathematics was geometry. Aim for more in less sentences. Amen!
Another set of notes: all questions are traps: the examiner wants you to think about what is asked. Think about the broader context around events. You may not have enough time to compare with contemporary perspectives. Put guideposts in your essay. Be careful about non sequiturs. Colons are good: they add emphasis (but use them carefully.) Short sentences!
Principia Mathematica
What a wonderful conference! There were a lot of talks and I should have taken more notes, but this is what I have, some quotes and sketches.
The algebraist versus the analyst. “Four riding in on a bicycle and then riding off again.” Numbers as moments, not an object (though it doesn’t lose generality.) “Cantor is hopeless at it.” (on zero.) “Do [numbers] start with 0 or 1? Yes and yes.” Frege and Russell finally give proper status to zero. The misreading of counting: does arithmetic start from counting? Number sequence is already in place, rather, we construct an isomorphism. There is a mistaken belief we count from one. Isomorphisms avoid counting, give proper status to zero, and sidestep the issue of how counting actually works (a transitive verb: pre-counting, we must decide what to count.) Contrary to popular depiction in Logicomix, Gödel and Russell did meet. Quine logic and Church logic. “It is not true that the square root of two is not irrational” requires every number be rational or irrational.
Why do we care about old people? How do we make progress in philosophy? Orders were syntactic rather than semantic: Kripke and Tarksi developed a hierarchy of truths. Free variable reasoning helped resolve nominala nd typical ambiguity: a scientific approach to a philosophical problem. “What nowadays constitutes research—namely, Googling it.” Nominal ambiguity: assert “x is even”, actually “forall x, x is even.” Quote: “It’s clear from the letter that he didn’t get past page five [of the Principia].” The word variable is deeply misleading, it’s not a variable name (progress!) “There are no undetermined men.” Anaphoric pronoun. We can’t express rules of inference this way.
Types: variables must have ranges. Hardly any theorems (all of the statements were schemas): we wanted to prove things about all types, but couldn’t on pain of contradiction. So all of the variables are type ically ambiguous. There is an argument in volume 2 respecting infinity, but a small world gives you the wrong mathematics (positivism.) But there was a bright idea:even if there aren’t enough things in the world, if there are k things, there are 2^k classes of things, etc. Go up the hierarchy. This is the interpretation for typical ambiguity. Whitehead thought theories were meaningless strings without types (a sort of macro in theory-land). ST made the language/metalanguage distinction!! “Seeing” is determining the type. The logocentric predicament is you’re supposed to use reasoning, but this reasoning is outside the formal system. Puns of operators on higher types, decorating all operators with a type label. The stratification of types.
Free variable reasoning is the same for typically ambiguous reasoning. Abbreviation for quantified reasoning (needs messy rules for inside quantifiers), indefinite names (can’t be the variable name, can’t lead to indefinite things), schematic names (lambdas: correct for variables, and modern for types.) But arguments that don’t convince someone unless they believe it (skepticism) sees: if the correct logic is type theoretic and oustide it, then we don’t have a position outside reasoning. (It’s a one way direction.) I think there is a way of talking about a system from within it. We have a weakened sense of truth: if you already believe it, it’s OK, but there is no convincing power.
The next lecture came from the computer scientist world. “Arguably, the more [programming languages] took from formal logic, the better it is.” Otherwise, it is the “ad-hoc craetion of electricians”. Computers allow easy formal manipulation and correctness checks. But for the mathematics? There isn’t very much of it. Proofs can be checked algorithmically (with formal inference rules). “Because there are many philosophers here, I hope I can answer questions in a suitably ambiguous manner.” Symbolism allows us to do “easy” things mechanically (Whitehead quote.) Do we need formal methods? In 1994 Pentium was found to have an error in floating point division. Robin’s conjecture was incorrectly proved. Different proof systems: de Bruijn generates proofs which are checked by a separate checker, LCF reduces all rules to primitive inferences checked by a logical kernel. After all, why don’t we prove that our proof assistants work? HOL Light (Principia) is only 430 lines of code. Schaffer’s joke: Ramseyfied Types. Right now, formal logic is on the edge of 20th century research mathematics, proofs needing “only 10k lines of code.” Maintenance of formal proofs is a big problem: we need intermediate declarative abstract models. Check out Flyspeck.
I had some scribblings in the margins: “references in logic?” (I think that’s linear logic), how about performance proofs (guaranteed to run in such-and-such time, realtime proofs), or probabilistically checkable proofs. Maybe complexity theory has something to say here.
Turing Machines
Their method of efficient access is… a zipper. Oh man!
GHC
My scribblings here are largely illegible, but it seems a few concepts initially gave me trouble:
- Stack layout, keeping up and down straight, info tables, and the motion of the stack pointer. I have a pretty good idea how this all works now, but in the beginning it was quite mysterious.
CmmNode constructors have a lot of field, and constructing a correspondence with printed C– is nontrivial.- Sizes of variables.
- Headers, payloads and code.
- Pointer tagging, esp. with respect to values living in registers, on the stack, and what the tag bits mean depending on context (functions or data). I never did figure out how the compacting GC worked.
This concludes the first notebook.
June 17, 2011I recently encountered the following pattern while writing some Haskell code, and was surprised to find there was not really any support for it in the standard libraries. I don’t know what it’s called (neither did Simon Peyton-Jones, when I mentioned it to him), so if someone does know, please shout out. The pattern is this: many times an endomorphic map (the map function is a -> a) will not make very many changes to the underlying data structure. If we implement the map straight-forwardly, we will have to reconstruct the entire spine of the recursive data structure. However, if we use instead the function a -> Maybe a, we can reuse old pieces of the map if there were no changes to it. (Regular readers of my blog may recognize this situation from this post.) So what is such an alternative map (a -> Maybe a) -> f a -> Maybe (f a) called?
One guess it might be the traverse function in Data.Traversable: it certainly has a very similar type signature: Applicative f => (a -> f b) -> t a -> f (t b). However, the semantics are subtly different, as you can see from this example:
Data.Traversable> traverse (\x -> if x == 2 then Just 3 else Nothing) [1,2,3]
Nothing
Recall that our function only returns Nothing in the event of no change. Thus, we should have gotten the result Just [1,3,3]: the first and third elements of the list unchanged, and the second element of the list with its new value.
How would we implement such a function for lists? Here’s a simple implementation:
nonSharingMap :: (a -> Maybe a) -> [a] -> Maybe [a]
nonSharingMap f xs = let (b, r) = foldr g (False, []) (zip xs (map f xs))
in if b then Just r else Nothing
where g (y, Nothing) (b, ys) = (b, y:ys)
g (_, Just y) (_, ys) = (True, y:ys)
But we can do better than this. Consider a situation where all elements of the list except the head stay the same:
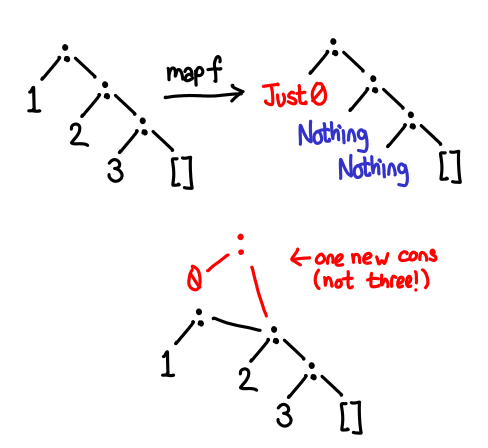
We would like to share the tail of the list between the old and new versions. With a little head-scratching, and the realization that tails shares, we can write this version:
sharingMap :: (a -> Maybe a) -> [a] -> Maybe [a]
sharingMap f xs = let (b, r) = foldr g (False, []) (zip3 (tails xs) xs (map f xs))
in if b then Just r else Nothing
where g (_, y, Nothing) (True, ys) = (True, y:ys)
g (_, _, Just y) (True, ys) = (True, y:ys)
g (ys', _, Nothing) (False, _) = (False, ys')
g (_, _, Just y) (False, ys) = (True, y:ys)
Open questions: what is this pattern called? Why doesn’t it follow the usual applicative structure? Does it fulfill some higher order pattern? Also, this scheme isn’t fully compositional: if I pass you a Nothing, you have no access to the original version in case there was a change elsewhere in the structure: (Bool, a) might be a little more compositional. Does this mean this is an example of the state monad? What about sharing?
Update. Anders Kaseorg writes in with a much more straight-forward, directly recursive version of the function:
sharingMap f [] = Nothing
sharingMap f (x : xs) = case (f x, sharingMap f xs) of
(Nothing, Nothing) -> Nothing
(y, ys) -> Just (fromMaybe x y : fromMaybe xs ys)
I haven’t checked, but one hope of expressing the function in terms of foldr and zip3 is that one may be able to get it to fuse. Of course, for actual recursive spine-strict data types, you usually won’t be able to fuse, and so a more straightforward presentation is more normal.
June 15, 2011I recently had to remove a number of type synonyms from the GHC code base which were along the lines of type CmmActuals = [CmmActual]. The process made me wonder a little about when type synonyms are appropriate for Haskell code. The Wikibooks article says type synonyms are “for making the roles of types clearer or providing an alias to, for instance, a complicated list or tuple type” and Learn You a Haskell says they “make more sense to someone reading our code and documentation.” But under what circumstances is this actually true?
Let’s try dividing the following use-cases of type synonyms:
- They can give extra semantic content, for example
DateString is more informative than String about its contents, though they are the same. - They can abbreviate long constructed types, for example
TcSigFun might abbreviate Name -> Maybe TcSigInfo.
The first is an example of code reader benefit: types with extra semantic information make it easier to see what a function is doing; the second is example of coder writer benefit: abbreviations of long types make writing type signatures more pleasurable. Sometimes a type synonym can give both benefits.
The downside of type signatures is their opacity of implementation. Seeing a value with type Address, I do not know if this is an algebraic data type or a type synonym, where as if it were a String I would know immediately what functions I could use on it. The type synonym adds an extra layer of indirection to figuring out how to manipulate the value: thus, it is a downside for the writer. It is true that algebraic data types and newtypes also add a layer of indirection, but they also bring to the table extra type safety that type synonyms don’t. (Furthermore, an algebraic data type is usually marvelously self documenting, as each of its constructors gets its own name).
I think my taste in the matter is as follows:
- Don’t use type synonyms if are not going to give any extra semantic information beyond the structure of the type.
- Synonyms for atomic types can be used freely, if the correspondence is unique. If you have many synonyms referring to the same atomic type, consider newtypes.
- Synonyms for non-function compound types should be used sparingly. They should not leak out of module boundaries, and are candidates for promotion into algebraic data-types.
- Synonyms for function compound types are mostly OK (since conversion into an ADT doesn’t buy you much, and they are unlikely to get mixed up), but make sure they are documented properly.
- Prefer to keep type synonyms inside module boundaries, un-exported. (Though, I know a few cases where I”ve broken this rule.)
How do you feel about type synonyms?
June 13, 2011There’s networking, and then there’s socialization. Networking is establishing the link, knowing how to find and talk to the person if the need arises. Socialization is communication for the sake of communication; it strengthens networks and keeps people in touch. In many ways, it is the utility a social networking site provides. Trouble is, there are so many different ways to communicate on the Internet these days. In this blog post, I try to explain the essential differences of socialization over the Internet. I believe what is called one-to-many socialization is the fundamental characteristic of the newest social patterns (facilitated by Facebook and Twitter), and describe some of the challenges in designing methods for consuming and aggregating this information.
There are a few obvious ways to slice up communication methods. Here are a few:
- Media. Most current applications are primarily text-based, but people have also tried audio, picture and video based modes with varying degrees of success.
- Length. How long is the average message in this medium?
- Persistence. If I ignore all activity older than an hour, how much do I miss? Are messages expected to be ephemeral or persistent? Is it even possible to send messages at all times?
- Distribution. Is it one-to-one, one-to-many or many-to-many communication? (For the purposes of this discussion, we’ll define on-to-many when there is an asymmetric flow of information: so a “comment” system does not turn a conversation into many-to-many… unless it manages to capture a conversation of its own.) When there are many listeners, how do we select who is listening?
- Consumption. How do we receive updates about communication?
We can look at a few existing networks and see how they answer these questions:
- Instant messaging (IM). Text, short length, persistent but not always available, one-to-one, consumed via a chat client. Note that with the existence of multi-protocol chat clients, it’s not too difficult to navigate the multitude or protocols employed by people all over the world.
- Internet Relay Chat (IRC) and Jabber. Text, short length, ephemeral, many-to-many, consumed via an IRC/Jabber client. There is some degree of integration between these protocols and instant messengers. Anyone can participate, but people can be kicked or banned from channels.
- Personal email. Text, medium length, persistent, one-to-one, consumed via a webmail interface or a mail client.
- Mailing lists. Text, medium length, persistent, many-to-many, consumed via webmail, mail client, or newsreader. For public mailing lists, anyone can participate.
- Forum. Text, medium length, persistent, many-to-many, consumed via web browser.
- Blog. HTML, medium to long length, persistent, one-to-many, consumed via web browser, possibly with an RSS reader. Anyone can subscribe to a public blog they are interested to.
- Twitter. Text, short length, ephemeral or persistent, one-to-many (though one-to-one communication is possible with at-replies, and in even more rare cases, many-to-many with multiple at-recipients), consumed via web browser or a Twitter client. Anyone can follow a public Twitter user.
- Facebook Wall. Text and images, short to medium length, ephemeral or persistent, one-to-many (but many-to-many with comments), consumed via web browser. Only friends can receive updates.
- Zephyr. (Sorry, had to sneak in an MIT example, since I use this protocol a lot.) Text, short to medium length, ephemeral or persistent, many-to-many (but with personal classes, which let people initiate conversations in a one-to-many fashion), consumed via zephyr client. Effectively limited to members of a university only.
- Social question websites. (e.g. Ask Reddit, Ask Hacker News, Stack Overflow.) Text, medium to long length, persistent, one-to-many (discussion itself can range from one-to-one to many-to-many), consumed via web browser. Updates are seen by subscribers of a given topic.
- Skype Voice/Video. Audio/video, short length, ephemeral, one-to-one, done via the Skype client.
There are a few interesting features about this current landscape that I can observe, once we have distilled these protocols down to these levels.
- Upstart companies attempting to create the next big social networks will frequently be innovating specifically in a few of these dimensions. Google Wave tried to innovate on medium, by introducing an extremely rich method of communication. Color is trying to innovate on medium and distribution.
- Communication protocols that lie within the same taxonomy (for example, IM clients) have seen a proliferation of clients that can interoperate before all of them. This has not, however, generally been the case for cross-taxonomy jumps: have you seen a single client which integrates participation with forums, email, Facebook and instant messaging? And if you have, did it work well at all? The method of consumption for one type of social information does not necessarily work well for other types.
- Similarly, it is not too difficult to bootstrap persistent communication protocols on other communication protocols. For example, a reply to a forum post is relatively persistent and not too much is lost if you send an email update whenever a new reply is found, and if you can’t rely on a user regularly checking your website for updates, this can be critical. However, sending instant messages to your email account makes no sense! There is something important here, which is that it does not make sense to mix ephemeral and persistent means of communication.
- Early social networking tools focused on one-to-one and many-to-many interactions, since these closely model how we socialize in real life. However, the advent of Twitter and Facebook has demonstrated that normal people can use a one-to-many medium not just for publishing (as was the case for blogs) but for socialization. People did not pin up sheets of gossip on noticeboards, they disseminated it via one-on-one conversations. But this is exactly what the new Internet is all about. The new social Internet involves exploring between the lines of publishing and private communication. Understanding what this variation is, is in many ways the key to understanding how to use the new social medium correctly.
As an end-user, I’m interested in mechanisms of unifying all social interaction methods which have the same consumption patterns—mostly because I don’t have a long enough attention span to deal with so many different website I have to check. And no, this does not mean just providing a tabbed interface which lets you switch from one network to another. Email and RSS work reasonably well for me for the persistent methods, but I have always found there to be a big void when it comes the new one-to-many styles of ephemeral (yet persistent) communication. Part of the reason is that we’re still trying to figure out what an optimal way of approaching this is, even when only one communication protocol is involved. (Remember that Facebook’s news feed was much loathed when it was originally released—but this was the key feature that moved Facebook from being a social networking site to a social communication site.) The situation becomes much more complex when multiple, subtly incompatible modes of communication are thrown into the mix.
Kyle Cordes writes about this topic from the perspective of a power user. I agree with him that it’s unclear whether or not there would actually be a market for such a unified social media client outside of power users. But it’s unclear to me if the open source community will step up to the bat and create such a client. I hope to be proven wrong.
June 10, 2011What is the biggest possible Haskell program that you could try debugging a space leak in? One very good choice is GHC, weighing in nearly a 100k lines of code (though, thankfully, 25% of that figure is comments.) Today, I’m going to describe one such space leak that I have fixed in GHC. This is not a full story: my code was ultimately the culprit, so not covered is how to debug code you did not write. However, I still like to think this story will cover some of the major points:
- How to setup a reproducible and manageable test-case for the leak,
- How to narrow down the source of the space leak,
- How to identify code is more prone to space leaking,
- How to determine what kind of leak it is,
- How to inspect libraries to determine if they are leaky, and
- How to test your fixes to see if they worked.
I really like this case because I had to do all of these things in order to pinpoint and ultimately fix this space leak. I hope you do too!
(Note: The diagrams are a bit big, because I generated them with hp2ps -c in order to make them look as close to what you might actually see in the field—as opposed to my hacked up copy of hp2pretty. Unfortunately, if I resized them, the text would be illegible. Suggestions welcome!)
Trouble in paradise
I first noticed something amiss when my builds of GHC with the new code generator enabled at stage 1 and 2 started OOM’ing. I’d come back after letting the build run, and notice that the build had failed on Parser.hs due to an out of memory. (In retrospect, the fact that the failure was from Parser.hs—a half a megabyte ball of autogenerated source code—should have been a good clue.) The first time, I didn’t think much of it: I re-ran the command manually, and it seemed to work. Perhaps I had gotten unlucky and some background process in my machine had been gobbling lots of memory while ghc-stage1 was running.
Of course, it happened again the next time I did a full build, and at that point I thought something a little fishy might have been going on. Because my normal testing did not uncover this problem, and because I did not relish having to spend time fixing a mysterious bug (most bugs in GHC are quite tricky devils to fix), I let things go for a few weeks. What had I done to merit such memory usage? I had no clue. Certainly the -hT profile (which I could easily add, since it doesn’t require you to recompile the program with profiling) wasn’t giving me much: a lot of thunks and integer maps (which, in GHC, are accessed using a wrapper module called UFM, or unique finite maps).
Setting up a test-case
When I finally got around to attacking this bug seriously, the first thing I wanted to do was make a reduced test-case of Parser.hs, effectively the input file that was causing the out-of-memory. Why not test on Parser.hs directly?
- Big inputs result in lots of data, and if you don’t really know what you’re looking for lots of data is overwhelming and confusing. The answer might be really obvious, but if there is too much cruft you’ll miss it.
- This was a file that was OOM-ing a machine with 2GB of RAM. Space is time, and Haskell programs that use this much memory take correspondingly longer to run. If I was looking to make incremental changes and re-test (which was the hope), waiting half an hour between iterations is not appealing.
- It was a strategy that had worked for me in the past, and so it seemed like a good place to start collecting information.
Actually, I cheated: I was able to find another substantially smaller test file lying around in GHC’s test suite that matched the heap profile of GHC when run on Parser.hs, so I turned my attentions there.
In your case, you may not have a “smaller” test case lying around. In that case, you will need to reduce your test-case. Fortunately, inputs that are not source programs tend to be a lot easier to reduce!
- Binary search for a smaller size. Your null hypothesis should be that the space leak has been caused strictly more data, so if you delete half of your input data, the leak should still be present, just not as severe. Don’t bother with anything sophisticated if you can chop and re-test.
- Sometimes a space leak is caused by a specific type of input, in which case deleting one half of the input set may cause the leak to go away. In this case, the first thing you should test is the other half of the input set: the culprit data is probably there, and you can continue binary searching on that chunk of code. In the worst case scenario (removing either half causes the leak to go away), buckle down and start selectively removing lines that you believe are “low risk.” If you remove a single line of data and the leak goes away, you have some very good data about what may actually be happening algorithmically.
- In the case of input data that has dependencies (for example, source code module imports), attempt to eliminate the dependencies first by re-creating them with stub data.
In the best case situation, this process will only take a few minutes. In the worst case situation, this process may take an hour or so but will yield good insights about the nature of the problem. Indeed, after I had gotten my new test-case, I reduced it even further, until it was a nice compact size that I could include in a blog post:
main = print $ length [
([0,0,0],0),([0,0,0],0),([0,0,0],0),([0,0,0],0),([0,0,0],0),
([0,0,0],0),([0,0,0],0),([0,0,0],0),([0,0,0],0),([0,0,0],0),
([0,0,0],0),([0,0,0],0),([0,0,0],0),([0,0,0],0),([0,0,0],0),
([0,0,0],0),([0,0,0],0),([0,0,0],0),([0,0,0],0),([0,0,0],0),
([0,0,0],0),([0,0,0],0),([0,0,0],0),([0,0,0],0),([0,0,0],0),
([0,0,0],0),([0,0,0],0),([0,0,0],0),([0,0,0],0),([0,0,0],0),
([0,0,0],0),([0,0,0],0),([0,0,0],0),([0,0,0],0),([0,0,0],0),
([0,0,0],0),([0,0,0],0),([0,0,0],0),([0,0,0],0),([0,0,0],0),
([0,0,0],0),([0,0,0],0),([0,0,0],0),([0,0,0],0),([0,0,0],0),
([0,0,0],0),([0,0,0],0),([0,0,0],0),([0,0,0],0),([0,0,0],0),
([0,0,0],0),([0,0,0],0),([0,0,0],0),([0,0,0],0),([0,0,0],0),
([0,0,0],0),([0,0,0],0),([0,0,0],0),([0,0,0],0),([0,0,0],0),
([0,0,0],0),([0,0,0],0),([0,0,0],0),([0,0,0],0),([0,0,0],0),
([0,0,0],0),([0,0,0],0),([0,0,0],0),([0,0,0],0),([0,0,0],0),
([0,0,0],0),([0,0,0],0),([0,0,0],0),([0,0,0],0),([0,0,0],0),
([0,0,0],0),([0,0,0],0),([0,0,0],0),([0,0,0],0),([0,0,0],0),
([0,0,0],0),([0,0,0],0),([0,0,0],0),([0,0,0],0),([0,0,0],0)]
A plain heap profile of looks very similar to the bigger Parser case, and even if it’s a different space leak, it’s still worth fixing.
Narrowing down the source
After you have your test case, the next step is to compile with profiling enabled. With GHC, this is as simple as switching your build settings to build a profiled stage 2 compiler; for a more ordinary Haskell project, all you need to do is add -prof -auto-all to your ghc invocation, or invoke Cabal with --enable-executable-profiling --enable-library-profiling --ghc-option=-auto-all. You may need to install profiling versions of your libraries, so a useful line to have in your .cabal/config file is library-profiling: True, which causes all libraries you cabal install or cabal configure to have profiling enabled. In fact, if you don’t have this setting on, turn it on right now. The extra time you spend when installing packages is well worth it when you actually want to profile something.
GHC has a large array of heap and time profiling options, but in general, the first two flags you want to try are -hc (for a traditional, cost-center based heap profile) and -prof (this gives a time profile—but we’ll see how this can be useful):
./ghc-stage2 -fforce-recomp -c Mu.hs +RTS -hc
./ghc-stage2 -fforce-recomp -c Mu.hs +RTS -prof
One quick remark: the program being tested here is ghc-stage2.hs (which is really big), not Mu.hs (which is really small.) I don’t actually care about what the output program is!
Here’s what the heap report tells us.
This is much better; rather than telling us what was on the heap, it tells us who put it on the heap. The main offenders seem to be mapUFM and mapUFM_Directly, which are utility functions mapping IntMap. But we also see that they are being called by two other functions. Their names have been truncated, but this is no problem: we can simply rerun the profiler with a longer cost center name using the -L flag:
./ghc-stage2 -fforce-recomp -c Mu.hs +RTS -hc -L50
Much better! You could have also consulted the prof file to find the primary callees of the offending functions:
individual inherited
COST CENTRE MODULE no. entries %time %alloc %time %alloc
middleAssignment CmmSpillReload 45804 5324 0.0 0.0 15.7 33.8
callerSaves StgCmmUtils 46347 8 0.0 0.0 0.0 0.0
wrapRecExpf CmmNode 46346 8 0.0 0.0 0.0 0.0
xassign CmmSpillReload 46345 8 0.0 0.0 0.0 0.0
foldUFM_Directly UniqFM 46344 4 0.0 0.0 0.0 0.0
mapUFM_Directly UniqFM 46343 1633 9.0 17.3 9.0 17.3
deleteSinks CmmSpillReload 45811 3524 0.0 0.0 0.0 0.0
invalidateUsersOf CmmSpillReload 45809 1887 0.0 0.0 6.7 16.4
regUsedIn CmmExpr 45821 6123 1.1 0.0 1.1 0.0
xassign CmmSpillReload 45820 6123 0.0 0.0 0.0 0.0
mapUFM UniqFM 45810 1887 5.6 16.4 5.6 16.4
Wondrous. We pull open the definitions for mapUFM, mapUFM_Directly, middleAssignment and invalidateUsersOf, all four of which constitute suspicious functions in which the space leak may lurk.
Use the source
Here I reproduce the relevant source code snippets. mapUFM and mapUFM_Directly are very thin wrappers around M, which is a qualified import for IntMap:
mapUFM f (UFM m) = UFM (M.map f m)
mapUFM_Directly f (UFM m) = UFM (M.mapWithKey (f . getUnique) m)
invalidateUsersOf is a relatively self-contained function:
-- Invalidates any expressions that use a register.
invalidateUsersOf :: CmmReg -> AssignmentMap -> AssignmentMap
invalidateUsersOf reg = mapUFM (invalidateUsers' reg)
where invalidateUsers' reg (xassign -> Just e) | reg `regUsedIn` e = NeverOptimize
invalidateUsers' _ old = old
middleAssignment is a bit trickier: it’s a very large function with many cases, but only one case has an invocation of mapUFM_Directly in it:
-- Algorithm for stores:
-- 1. Delete any sinking assignments that were used by this instruction
-- 2. Look for all assignments that load from memory locations that
-- were clobbered by this store and invalidate them.
middleAssignment (Plain n@(CmmStore lhs rhs)) assign
= mapUFM_Directly p . deleteSinks n $ assign
where p r (xassign -> Just x) | (lhs, rhs) `clobbers` (r, x) = NeverOptimize
p _ old = old
I would like to remark how small the amount of code we have to look at is. If they were much larger, one sensible thing to do would have been to instrument manually with more SCC pragmas, so that you can figure out what local definition to zoom in on. Once you have a small segment of code like this, one of the best ways to proceed is debugging by inspection: that is, stare at the code until the bug becomes obvious.
A thunk leak?
If you’ve ever fixed a space leak in Haskell before, or have been reading this blog regularly, there should be an obvious first guess: mapUFM is too lazy, and we are thus accumulating thunks. This is consistent with the presence of thunks in our initial heap profiles. A keen reader may have noticed that the thunks aren’t present in our hc profile, because thunks are not cost-centers. We can verify that they’re still hanging around, though, by running an hd profile:
./ghc-stage2 -fforce-recomp -c Mu.hs +RTS -hd
That sat_s5zO is the precise thunk from IntMap that is leaking. A quick look at the source code of IntMap confirms our suspicion:
data IntMap a = Nil
| Tip {-# UNPACK #-} !Key a
| Bin {-# UNPACK #-} !Prefix
{-# UNPACK #-} !Mask
!(IntMap a) !(IntMap a)
mapWithKey :: (Key -> a -> b) -> IntMap a -> IntMap b
mapWithKey f = go
where
go (Bin p m l r) = Bin p m (go l) (go r)
go (Tip k x) = Tip k (f k x)
go Nil = Nil
IntMap is spine-strict, but mapWithKey (which is invoked , lacking any bang-patterns, is clearly lazy in the update function f. Annoyingly enough, it seems that there is no strict version of the function either. Well, let’s quickly add a strict version of this function and test it out:
mapWithKey' f t
= case t of
Bin p m l r -> Bin p m (mapWithKey' f l) (mapWithKey' f r)
Tip k x -> let v = f k x in v `seq` Tip k v
Nil -> Nil
After a recompile, we see the following results with -hc:
Uh oh! The memory usage improved slightly, but it still looks pretty bad. Did we do something wrong? Let’s find out what the objects on the heap actually look like with -hd:
Notice that the thunks have disappeared from the profile! The fix was successful: we’ve eliminated the thunks. Unfortunately, none of the IntMap constructors Bin or Tip have gone away, and those are the true space leaks. So what’s holding on to them? We can use retainer profiling with -hr:
This is not a space leak. In fact, it may very well be a problem with the algorithm we are using. We discard our thunk leak hypothesis, and go back to the drawing board.
Lack of sharing
I will admit, when I got to this point of the debugging, I was pretty displeased. I thought I had pinned down the space leak, but swapping in a strict map hadn’t helped at all. Instead, all of the maps were being retained by the dataflow pass stage, and I knew I couldn’t eliminate those references, because that was how the algorithm worked. The dataflow analysis algorithm in GHC needs to retain the map it calculates for a given node, because the map is necessary for performing rewrites at every point of the graph, and may be reused in the event of a loop. It would take substantial cleverness to use the map in a non-persistent way.
But it seemed fairly unlikely that this code was strictly to blame, since we had used it with great success in many other parts of the code. Then I had an insight. The map in IntMap does not perform any sharing at all with the original structure: it needs to reconstruct all of the internal nodes. When the function being mapped over the structures preserves the original value of most of the map entries, this is quite wasteful. So perhaps a better strategy would be to pre-calculate which map entries changed, and only update those entries. If no inserts are made, the map gets completely shared; if one insert is made, the majority of the map continues to be shared (only the path is rewritten.) The rewritten functions then look as follows:
invalidateUsersOf reg m = foldUFM_Directly f m m
where f u (xassign -> Just e) m | reg `regUsedIn` e = addToUFM_Directly m u NeverOptimize
f _ _ m = m
middleAssignment (Plain n@(CmmStore lhs rhs)) assign
= let m = deleteSinks n assign
in foldUFM_Directly f m m
where f u (xassign -> Just x) m | (lhs, rhs) `clobbers` (u, x) = addToUFM_Directly m u NeverOptimize
f _ _ m = m
Guess what: it worked!
Optimistic, I spun up a new full compile, and most gratifyingly, it did not out-of memory. Victory!
Conclusion
The point of this post was not to show you how lack of sharing could cause the space usage of an algorithm to blow up—delving into this topic in more detail is a subject for another post. The point was to demonstrate how GHC’s profiling tools can really home in on the source of a leak and also let you know if your fixes worked or not. Ultimately, fixing space leaks is a lot like debugging: after you’ve checked the usual culprits, every situation tends to be different. (Of course, check the usual culprits first! They might work, unlike in this situation.)
In particular, I want to emphasize that just because one particular fix didn’t work, doesn’t mean that the leak isn’t still in the location indicated by profiling. The ultimate fix was still in the very same place as the profiling suggested, and checking the retainers also indicated the algorithm that was ultimately tickling a lack of sharing. Furthermore, once you have a reduced test-case that exhibits the leak, making small changes and seeing how the heap usage changing is extremely fast: even for a huge codebase like GHC, a small source level change only results in a ten second recompile, and getting fresh heap statistics only takes another five seconds. This is fast and allows you to experiment.
Now go forth, and slay space bugs in even the largest programs without fear!
June 8, 2011Today we continue the theme, “What can Philosophy of Science say for Software Engineering,” by looking at some topics taken from the Philosophy of Physical Sciences.
Measurement and quantification
Quantification is an activity that is embedded in modern society. We live by numbers, whether they are temperature readings, velocity, points of IQ, college rankings, safety ratings, etc. Some of these are uncontroversial, others, very much so, and a software engineer must always be careful about numbers they deal in, for quantification is a very tricky business.
Philosophers of science can look to history for some insight into this conundrum, for it was not always the case that thermometry was an uncontroversial method of generating numbers. While the thermometer itself was invented in the 16th century, it took centuries to establish the modern standard of measuring temperature. What made this so hard? Early dabblers in thermometry were well aware of the ability to calibrate a thermometer by testing its result at various fixpoints (freezing and boiling), and graduating the thermometer accordingly, and for some period of times this was deemed adequate for calibrating thermometers.
But alas, the thermal expansion of liquids is not uniform across liquids, and what intrepid experimenters like Herman Boerhaave and Daniel Fahrenheit discovered was, in many cases, two thermometers would not agree with each other, even if they had been calibrated in the same way. How would they determine which thermometer was more accurate, without appealing to… another thermometer? Most justifications involving the nature of the liquid “particles” and their forces appealed to (at the time) unjustifiable theoretical principles.
Without the invention of modern thermodynamics, the most compelling case would be put forth Henri Victor Regnault. An outstanding experimentalist, Regnault set forth to solve this problem by systematically eliminating all theoretical assumptions from this work: specific heat, caloric, conservation of heat—all of these did not matter to him. What Regnault cared about was the comparability of thermometers: an instrument that gave varying values depending on the situation could not be trusted. If the thermometer was sensitive to the proportion of alcohol in it, or the way its glass had been blown, it was not to be taken as reflecting reality.
In the face of uncertainty and unsure theoretical basis, even simple criterion like comparability can be useful in getting a grip on the situation. One should not underestimate the power of this technique, due in part to its ability to operate without assuming any sort of theoretical knowledge of the task at hand.
Reductive explanations
The law of leaky abstractions states that all attempts to hide the low-level details of a system fail in some way or another. Taken to the extreme, it results in something resembling a reductive approach to the understanding of computer systems: in order to understand how some system works, it is both desirable and necessary to understand all of the layers below it.
Of course, we make fun of this sort of reductivism when we say things like, “Real men program with a magnet on their hard drive.” One simply cannot be expected to understand a modern piece of software merely by reading all of the assembly it is based on. Even systems that are written at a low level have implicit higher level structure that enables engineers to ignore irrelevant details (unless, of course, those irrelevant details are causing bugs.)
This situation is fascinating, because it is in many senses the opposite of the reductivism debate in science. For software, many aspects of the end behavior of a system can be deductively known from the very lowest level details—we simply know that this complexity is too much for a human. Science operates in the opposite direction: scientists seek simplifying, unifying principles as the delve deeper into more fundamental phenomena. Biology is applied chemistry, chemistry is applied physics, physics is applied quantum mechanics, etc. Most scientists hold the attitude of ontological reduction: anything we interact with can eventually be smashed up into elementary particles.
But even if this reduction is possible, it may not mean we can achieve such a reduction in our theories. Our theories at different levels may even contradict one another (so called Kuhnian incommensurability), and yet these theories approximate and effective. So is constantly pursuing a more fundamental explanation a worthwhile pursuit in science, or, as a software engineer might think, only necessary in the case of a leaky abstraction?
Postscript. My last exam is tomorrow, at which point we will return to our regularly scheduled GHC programming.
June 6, 2011I spent part of my year in Cambridge reading the History and Philosophy of Science course. It has been a thrilling and enlightening course, and I cannot recommend it highly enough for anyone lucky enough to take the HPS strand at Cambridge. Of course, I was a bit of an odd one out, since the course is designed for Natural Science majors, and I am, of course, a Computer Scientist.
In the next two posts, I’d like to highlight some of the major themes of the Philosophy of Science course, and how they may be applicable to software engineers. (Notably not computer scientists: it seems likely that their philosophy is one rooted in the Philosophy of Maths.) Not all of the questions are relevant: an old tripos question asks “Is there a unified philosophy of science, or disparate philosophies of the sciences?”—I would likely answer “both.” But I think the existing corpus of knowledge can give some insights to some tenacious questions facing us: What constitutes the cause of a bug? How does a software engineer debug? How do we know if a particular measurement or assessment of software is reliable? What reason do we have for extending our realm of experience with a software to areas for which we have no experience? Can all explanations about the high-level behavior of code be reduced to the abstractions behind them? I should be careful not to overstate my case: undoubtedly some of you may think some of these questions are not interesting at all, and others may think the arguments I draw in not insightful at all. I humbly ask for your patience—I am, after all, being examined on this topic tomorrow.
Causation
What does it mean when we say an event causes another? This is one of those questions that seem so far removed from practicality to be another one of those useless philosophical exercises. But the answer is not so simple. The philosopher David Hume observes that when we speak of causation, there is some necessary connection between the cause and effect: the bug made the program crash. But can we ever observe this “necessary connection” directly? Hume argues no: we only ever see a succession of one event to another; unlike the programmer, we cannot inspect the source code of the universe and actually see “Ah yes, there’s the binding of that cause to that effect.”
One simple model of causation is the regularity theory, inspired by a comment Hume makes in the Enquiry: a cause is “an object, followed by another, and where all the objects similar to the first are followed by objects similar to the second.” I observe that every event of “me pressing the button” is immediately followed by “the program crashing”, then I might reasonably infer that pressing the button is the cause of the crash. There is nothing unreasonable here, but now the philosopher sees the point of attack. There are many, many cases where such a simple regularity theory fails. Consider the following cases:
- I press the button, but the program only crashes some of the time. Even if the bug is not 100% reproduceable, I might still reasonably say it causes the crash.
- An alert dialog pops up, I press the button, and the program crashes. But it was not my pressing the button that caused the crash: rather, it’s more likely it was whatever caused the alert dialog to pop up. (You may have had an experience explaining this to a less computer-savvy family member.)
- I have only pressed the button once, and that one time the program crashed. It is indeed the case that whenever I pushed the button, a crash came afterwards: but it’s possible for me to press the button now and no crash to occur.
Perhaps no reasonably practiced software engineer uses this model of causation. Here is a more plausible model of causation, the counterfactual model (proposed by David Lewis). Here we pose a hypothetical “if” question: if pushing the button causes a crash, we may equally say “if the button had not been pressed, then the crash would not have happened.” As an exercise, the reader should verify that the above cases are neatly resolved by this improved model of causality. Alas, the counterfactual model is not without its problems as well:
- Suppose that our crashing program has two bugs (here we use “bug” in the sense of “source code defect”). Is it true that the first bug causes the crash? Well, if we removed that bug, the program would continue to crash. Thus, under the counterfactual theory of causation, the first bug doesn’t cause the crash. Neither does the second bug, for that matter. We have a case of causal overdetermination. (Lewis claims the true cause of the bug is the disjunction of the two bugs. Perhaps not too surprising for a computer scientist, but this sounds genuinely weird when applied to every-day life.)
- Suppose that our crashing program has a bug. However, removing the first bug exposes a latent bug elsewhere, which also causes crashes. It’s false to say removing the first bug would cause the crashing to go away, so it does not cause the crash. This situation is called causal preemption. (Lewis’s situation here is to distinguish between causal dependence and causal chains.)
What a software engineer realizes when reading these philosophers is that the convoluted and strange examples of causation are in fact very similar to the knots of causality he is attached to on a day-to-day basis. The analysis here is not too complicated, but it sets the stage for theories of laws of nature, and also nicely introduces the kind of philosophical thinking that encourages consideration of edge-cases: a virtuous trait for software engineers!
Methodology and confirmation
One of the most famous debates in philosophy of science to spill over into popular discourse is the debate on scientific methodology—how scientists carry out their work and how theories are chosen. I find this debate has direct parallels into the art of debugging, one of the most notoriously difficult skills to teach fledgling programmers. Here we’ll treat two of the players: inductivism (or confirmation theory) and falsificationism (put forth by Karl Popper.)
Sherlock Holmes once said this about theories: “Insensibly one begins to twist facts to suit theories, instead of theories to suit facts.” He advocated an inductivist methodology, in which the observer dispassionately collects before attempting to extract some pattern of them—induction itself is generalization from a limited number of cases. Under this banner, one is simply not allowed to jump to conclusions while they are still collecting data. This seems like a plausible thing to ask of people, especially perhaps profilers who are collecting performance data. The slogan, as A.F. Chalmers puts it, is “Science is derived from facts.”
Unfortunately, it is well known among philosophers of science that pure inductivism is deeply problematic. These objects range from perhaps unresolvable foundational issues (Hume’s problem of induction) to extremely practical problems regarding what scientists actually practice. Here is a small sampling of the problems:
- What are facts? On one level, facts are merely sense expressions, and it’s an unreasonable amount of skepticism to doubt those. But raw sense expressions are not accessible to most individuals: rather, they are combined with our current knowledge and disposition to form facts. An expert programmer will “see” something very different from an error message than a normal end-user. Fact-gathering is not egalitarian.
- Facts can be fallible. Have you ever analyzed a situation, derived some facts from it, only to come back later and realize, wait, your initial assessment was wrong? The senses can lie, and even low-level interpretations can be mistaken. Inductivism doesn’t say how we should throw out suspicious facts.
- Under what circumstances do we grant more weight to facts? The inductivist says that all facts are equal, but surely this is not true: we value more highly facts which resulted from public, active investigation, than we do facts that were picked up from a private, passive experience. Furthermore, an end-user may report a plethora of facts, all true, which an expert can instantly identify as useless.
- And, for a pure bit of philosophy, the problem of induction says that we have no reason to believe induction is rational. How do we know induction works? We’ve used in the past successfully. But the act of generalizing this past success to the future is itself induction, and thus the justification is circular.
This is not to say that inductivism cannot be patched up to account for some of these criticisms. But certainly the simple picture is incomplete. (You may also accuse me of strawman beating. In an educational context, I don”t think there is anything wrong here, since the act of beating a strawman can also draw out weaknesses in more sophisticated positions—the strawman serves as an exemplar for certain types of arguments that may be employed.)
Karl Popper proposed falsificationism as a way to sidestep the issues plaguing induction. This method should be another one that any software engineer should be familiar with: given a theory, you then seek an observation or experiment that would falsify it. If it is falsified, it is abandoned, and you search for another theory. If it is not, you simply look for something else (Popper is careful to say that we cannot say that the theory was confirmed by this success).
Falsification improves over inductivism by embracing the theory-dependence of observation. Falsificationists don’t care where you get your theory from, as long as you then attempt to falsify it, and also accept the fact that there is no way to determine if a theory is actually true in light of evidence. This latter point is worth emphasizing: whereas induction attempts to make a non-deductive step from a few cases to a universal, falsification can make a deductive step from a negative case to a negative universal. To use a favorite example, it is logically true that if there is a white raven, then not all ravens are black. Furthermore, a theory is better if it is more falsifiable: it suggests a specific set of tests.
As might be expected, naive falsificationism has its problems too, some which are reminiscent of some problems earlier.
- In light of a falsification, we can always modify our theory to account for this particular falsifying instance. This is the so-called ad hoc modification. “All ravens are black, except for this particular raven that I saw today.” Unfortunately, ad hoc modifications may be fair play: after all, there is no reason why software cannot be modified for a particular special case. Better crack open the source code.
- Falsificationism suggests we should always throw out a theory once we have seen falsifying evidence. But as we saw for inductivism, evidence can be wrong. There are many historic cases where new theories were proposed, and it was found that they didn’t actually fit the evidence at hand (Copernicus’s heliocentric model of the universe was one—it did no better than the existing Ptolemaic model at calculating where the planets would be.) Should these new theories have been thrown out? Real scientists are tenacious; they cling to theories, and many times this tenacity is useful.
- To turn this argument on its head, it is never the case that we can test a theory in isolation; rather, an experimental test covers both the theory and any number of auxiliary assumptions about the test setup. When a falsifying test is found, any one of the theory or auxiliary assumptions may be wrong—but we don’t know which! The Duhem-Quine thesis states that given any set of observations, we are always able to modify the auxiliary assumptions to make our theory fit (this thesis may or may not be true, but it is interesting to consider.)
All of these problems highlight how hard it is to come up with an accurate account of what is called the “scientific method.” Simple descriptions do not seem to be adequate: they sound intuitively appealing but have downsides. The practicing scientist is something of an opportunist: he does what works. So is the debugger.
Next time, I hope to talk about quantification, measurement and reduction.