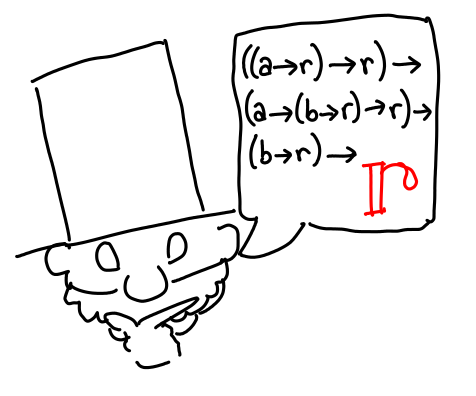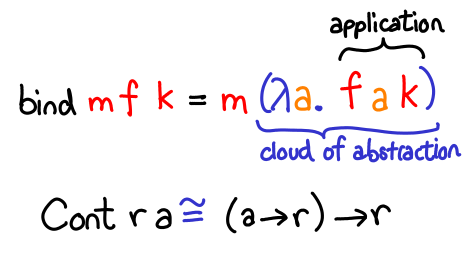September 26, 2011The opinions presented in this post are not necessarily mine. I’m just one very confused undergraduate senior with a lot of soul searching to do.
When I tell my friends, “I’m going to get a PhD,” I sometimes get the response, “Good for you!” But other times, I get the response, “Why would you want to do that?” as if I was some poor, misguided soul, brainwashed by a society which views research as the “highest calling”, the thing that the best go to, while the rest go join industry. “If you’re a smart hacker and you join industry,” they say, “you will have more fun immediately, making more impact and more money.”
Time. Getting a PhD takes a lot of time, they tell me. Most programs like to advertise something like five, or maybe six years, but if you actually look at the statistics, it’s actually something that could potentially extend up to nine or ten years. That’s a really huge chunk of your life: effectively all of your twenties and, honestly, there might be much better things for you to do with these tender years of your life. A PhD is merely a stepping stone, a necessary credential to be taken seriously in academia but not anything indicative of having made a significant contribution to a field. And for a stepping stone, it’s an extremely time consuming one.
There are many other things that could have happened during this time. You could have began a startup and seen it get acquired or sink over a period of three years: six years seems like two lifetimes in a context like that. You could have began a career as a professional in an extremely hot job market for software engineers, hopping from job to job until you found a work that you were genuinely interested in: as a PhD you are shackled to your advisor and your university. The facilities for change are so incredibly heavyweight: if you switch advisors you effectively have to start over, and it’s easy to think, “What did I do with the last three years of my life?”
Money. There is one thing you didn’t do in those last few years: make money. PhDs are the slave labor that make the academic complex run. It’s not that universities aren’t well funded by grants: indeed, the government spends large amounts of money funding research programs. But most of this money never finds its way to PhDs: you’re looking at a $30k stipend, when a software engineer can easily be making $150k to $200k in a few years at a software company. Even once you make it into a tenure track position, you are still routinely making less than people working for industry. You don’t go into academia expecting to get rich.
Scarcity. Indeed, you shouldn’t go into academia expecting to get much of anything. The available tenured positions are greatly outstripped by the number of PhD applicants, to the point that your bid into the academic establishment is more like a lottery ticket. You have to be doing a postdoc—e.g. in a holding pattern—at precisely the right time when a tenure position becomes vacated (maybe the professor died), or spend years building up your network of contacts in academia in hopes of landing a position through that connection. Most people don’t make it, even at a second or third tier university. The situation is similar for industrial research labs, which become rarer and rarer by the year: Microsoft Research is highly selective and as a prospective PhD, you are making a ten year bet about its ability to survive. Intel Labs certainly didn’t.
Tenure isn’t all that great. But even if you do make it to tenure, it isn’t actually all that great. You’ve spent the last decade and a half fighting for the position in a competitive environment that doesn’t allow for any change of pace (god forbid you disappear for a year while your tenure clock is ticking), and now what? You are now going to stay at the institution you got tenure at for the rest of your life: all you might have is a several month sabbatical every few years. It’s the ivory handcuffs, and you went through considerably more effort to put them on than that guy who went to Wall Street. And as for the work? Well, you still have to justify your work and get grant funding, you still need to serve on committees and do other tasks which you simply must do which are not at all related to your research. In industry, you could simply hire someone to handle your post on your university’s “Disciplinary Committee”—in academia, that’s simply not how it works.
Lack of access. And if you are a systems researcher, you don’t even get the facilities you need to do the large-scale research that is really interesting. Physicists get particle accelerators, Biologists get giant labs, but what does the systems researcher get? Certainly not a software system used by millions of users around the world. To get that sort of system, you have to go to industry. Just ask Matt Welsh, who made a splash leaving a tenured position at Harvard to go join Google. Working in this context lets you actually go and see if your crazy ideas go and work.
Don’t do it now. Of course, at this point I’m mentally protesting that this is all incredibly unfair to a PhD, that you do get more freedom, that maybe some people don’t care that much about money, that this is simply a question about value systems, and really, for some people, it’s the right decision. I might say that your twenties are also the best time to do your PhD, that academia is the correct late-career path, that you can still do a startup as a professor.
Perhaps, they say, but you need to figure out if this is the right decision for you. You need experience in both areas to make this decision, and the best time to do this is sampling industry for two or three years before deciding if you want to go to industry. After you graduate your PhD, people mentally set their timer on your potential as an academic, and if you don’t publish during that time people will stop taking you seriously. But if you start a PhD in your mid-twenties, no one will bat an eye. Everyone can have a bad software internship; don’t let that turn you away from industry. We solve cool problems. We are more diverse, in aggregate we give more freedom. In no sense of the word are we second-class.
They might be right. I don’t know.
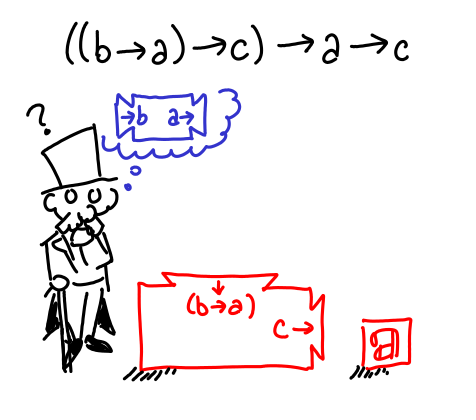
September 5, 2011Ever wondered how Haskellers are magically able to figure out the implementation of functions just by looking at their type signature? Well, now you can learn this ability too. Let’s play a game.
You are an inventor, world renowned for your ability to make machines that transform things into other things. You are a proposer.

But there are many who would doubt your ability to invent such things. They are the verifiers.

The game we play goes as follows. You, the proposer, make a claim as to some wondrous machine you know how to implement, e.g. (a -> b) -> a -> b (which says given a machine which turns As into Bs, and an A, it can create a B). The verifier doubts your ability to have created such a machine, but being a fair minded skeptic, furnishes you with the inputs to your machine (the assumptions), in hopes that you can produce the goal.
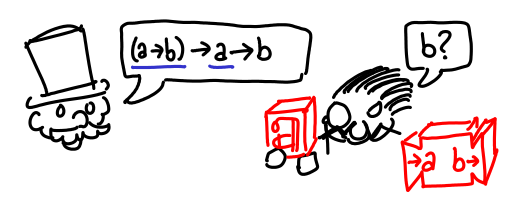
As a proposer, you can take the inputs and machines the verifier gives you, and apply them to each other.
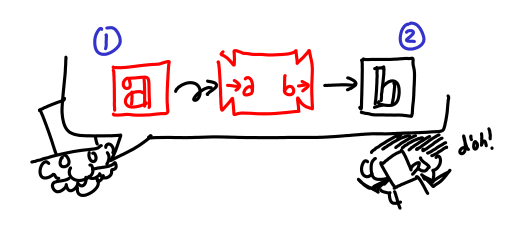
But that’s not very interesting. Sometimes, after the verifier gives you some machines, you want to make another proposal. Usually, this is because one of the machines takes a machine which you don’t have, but you also know how to make.
The verifier is obligated to furnish more assumptions for this new proposal, but these are placed inside the cloud of abstraction.
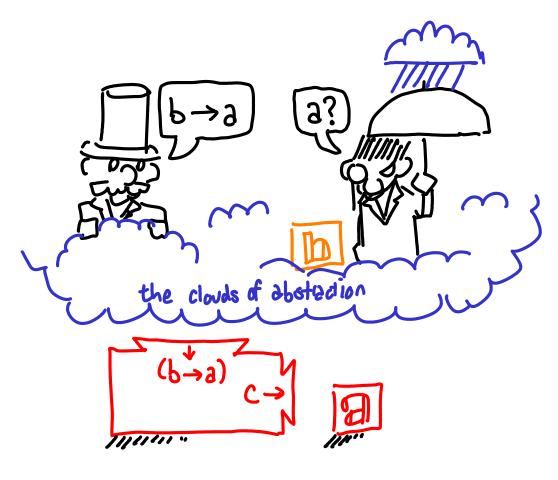
You can use assumptions that the verifier furnished previously (below the cloud of abstraction),

but once you’ve finished the proposal, all of the new assumptions go away. All you’re left with is a shiny new machine (which you ostensibly want to pass to another machine) which can be used for the original goal.
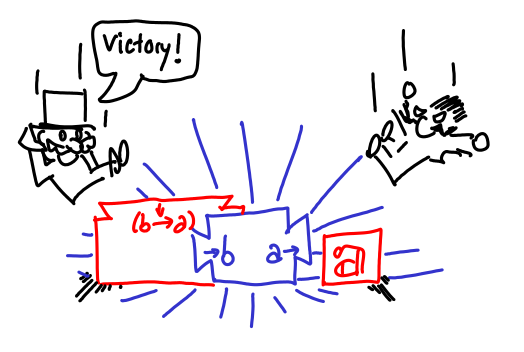
These are all the rules we need for now. (They constitute the most useful subset of what you can do in constructive logic.)
Let’s play a game.
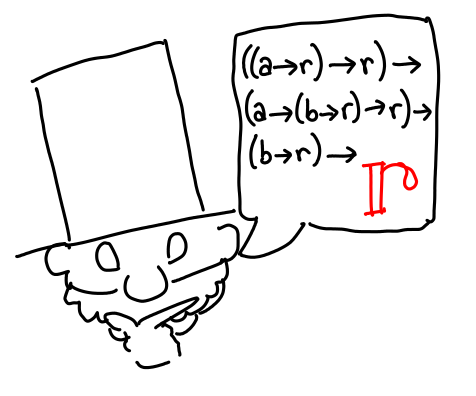
Our verifier supplies the machines we need to play this game. Our goal is r.
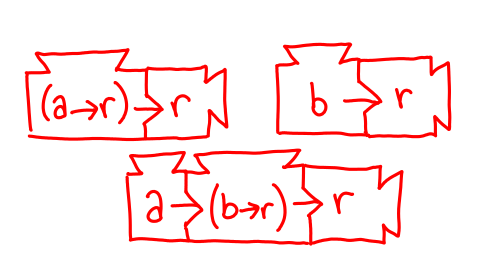
That’s a lot of machines, and it doesn’t look like we can run any of them. There’s no way we can fabricate up an a from scratch to run the bottom one, so maybe we can make a a -> r. (It may seem like I’ve waved this proposal up for thin air, but if you look carefully it’s the only possible choice that will work in this circumstance.) Let’s make a new proposal for a -> r.
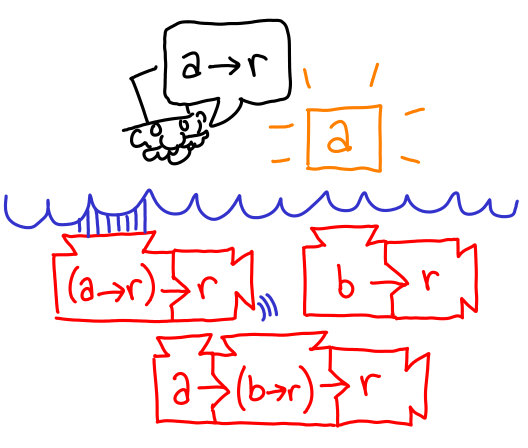
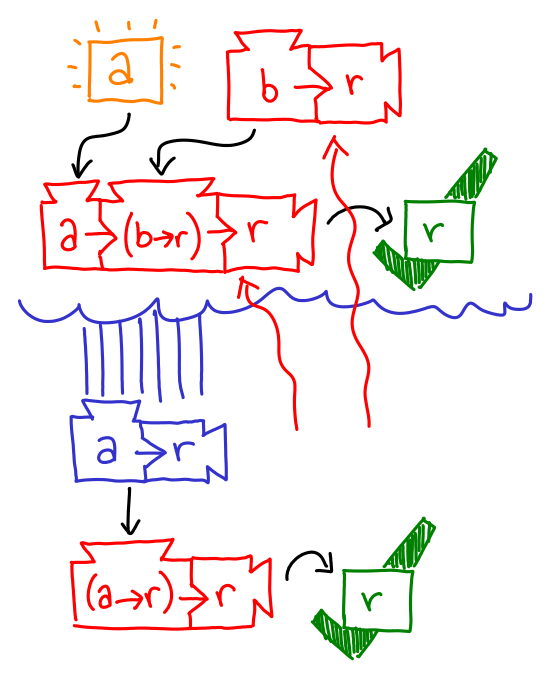
Our new goal for this sub-proposal is also r, but unlike in our original case, we can create an r with our extra ingredient: an a: just take two of the original machines and the newly furnished a. Voila, an r!
This discharges the cloud of abstraction, leaving us with a shiny new a -> r to pass to the remaining machine, and fulfill the original goal with.
Let’s give these machines some names. I’ll pick some suggestive ones for you.
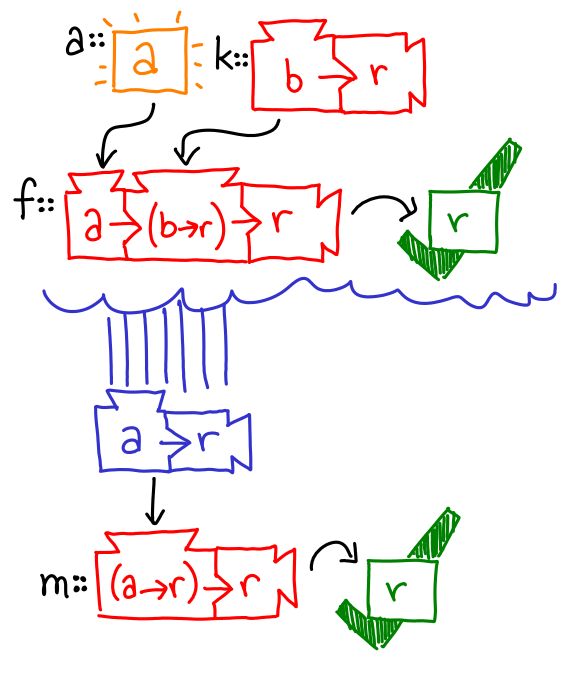
Oh hey, you just implemented bind for the continuation monad.
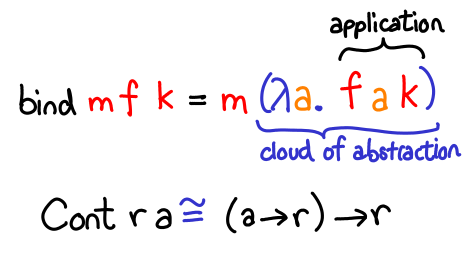
Here is the transformation step by step:
m a -> (a -> m b) -> m b
Cont r a -> (a -> Cont r b) -> Cont r b
((a -> r) -> r) -> (a -> ((b -> r) -> r)) -> ((b -> r) -> r)
((a -> r) -> r) -> (a -> (b -> r) -> r) -> (b -> r) -> r
The last step is perhaps the most subtle, but can be done because arrows right associate.
As an exercise, do return :: a -> (a -> r) -> r (wait, that looks kind of familiar…), fmap :: (a -> b) -> ((a -> r) -> r) -> (b -> r) -> r and callCC :: ((a -> (b -> r) -> r) -> (a -> r) -> r) -> (a -> r) -> r (important: that’s a b inside the first argument, not an a !).
This presentation is the game semantic account of intuitionistic logic, though I have elided treatment of negation and quantifiers, which are more advanced topics than the continuation monad, at least in this setting.
August 29, 2011In 2007, Eric Kidd wrote a quite popular article named 8 ways to report errors in Haskell. However, it has been four years since the original publication of the article. Does this affect the veracity of the original article? Some names have changed, and some of the original advice given may have been a bit… dodgy. We’ll take a look at each of the recommendations from the original article, and also propose a new way of conceptualizing all of Haskell’s error reporting mechanisms.
I recommend reading this article side-to-side with the old article.
No change. My personal recommendation is that you should only use error in cases which imply programmer error; that is, you have some invariant that only a programmer (not an end-user) could have violated. And don’t forget, you should probably see if you can enforce this invariant in the type system, rather than at runtime. It is also good style to include the name of the function which the error is associated with, so you say “myDiv: division by zero” rather than just “Division by zero.”
Another important thing to note is that error e is actually an abbreviation for throw (ErrorCall e), so you can explicitly pattern match against this class of errors using:
import qualified Control.Exception as E
example1 :: Float -> Float -> IO ()
example1 x y =
E.catch (putStrLn (show (myDiv1 x y)))
(\(ErrorCall e) -> putStrLn e)
However, testing for string equality of error messages is bad juju, so if you do need to distinguish specific error invocations, you may need something better.
No change. Maybe is a convenient, universal mechanism for reporting failure when there is only one possible failure mode and it is something that a user probably will want to handle in pure code. You can easily convert a returned Maybe into an error using fromMaybe (error "bang") m. Maybe gives no indication what the error was, so it’s a good idea for a function like head or tail but not so much for doSomeComplicatedWidgetThing.
I can’t really recommend using this method in any circumstance. If you don’t need to distinguish errors, you should have used Maybe. If you don’t need to handle errors while you’re in pure code, use exceptions. If you need to distinguish errors in pure code, for the love of god, don’t use strings, make an enumerable type!
However, in base 4.3 or later (GHC 7), this monad instance comes for free in Control.Monad.Instances; you no longer have to do the ugly Control.Monad.Error import. But there are some costs to having changed this: see below.
If you at all a theoretician, you reject fail as an abomination that should not belong in Monad, and refuse to use it.
If you’re a bit more practical than that, it’s tougher to say. I’ve already made the case that catching string exceptions in pure code isn’t a particularly good idea, and if you’re in the Maybe monad fail simply swallows your nicely written exception. If you’re running base 4.3, Either will not treat fail specially either:
-- Prior to base-4.3
Prelude Control.Monad.Error> fail "foo" :: Either String a
Loading package mtl-1.1.0.2 ... linking ... done.
Left "foo"
-- After base-4.3
Prelude Control.Monad.Instances> fail "foo" :: Either String a
*** Exception: foo
So you have this weird generalization that doesn’t actually do what you want most of the time. It just might (and even so, only barely) come in handy if you have a custom error handling application monad, but that’s it.
It’s worth noting Data.Map does not use this mechanism anymore.
MonadError has become a lot more reasonable in the new world order, and if you are building your own application monad it’s a pretty reasonable choice, either as a transformer in the stack or an instance to implement.
Contrary to the old advice, you can use MonadError on top of IO: you just transform the IO monad and lift all of your IO actions. I’m not really sure why you’d want to, though, since IO has it’s own nice, efficient and extensible error throwing and catching mechanisms (see below.)
I’ll also note that canonicalizing errors that the libraries you are interoperating is a good thing: it makes you think about what information you care about and how you want to present it to the user. You can always create a MyParsecError constructor which takes the parsec error verbatim, but for a really good user experience you should be considering each case individually.
It’s not called throwDyn and catchDyn anymore (unless you import Control.OldException), just throw and catch. You don’t even need a Typeable instance; just a trivial Exception instance. I highly recommend this method for unchecked exception handling in IO: despite the mutation of these libraries over time, the designers of Haskell and GHC’s maintainers have put a lot of thought into how this exceptions should work, and they have broad applicability, from normal synchronous exception handling to asynchronous exception handling, which is very nifty. There are a load of bracketing, masking and other functions which you simply cannot do if you’re passing Eithers around.
Make sure you do use throwIO and not throw if you are in the IO monad, since the former guarantees ordering; the latter, not necessarily.
No reason to use this, it’s around for hysterical raisins.
This is, for all intents and purposes, the same as 5; just in one case you roll your own, and in this case you compose it with transformers. The same caveats apply. Eric does give good advice here shooing you away from using this with IO.
Here are some new mechanisms which have sprung up since the original article was published.
Pepe Iborra wrote a nifty checked exceptions library which allows you to explicitly say what Control.Exception style exceptions a piece of code may throw. I’ve never used it before, but it’s gratifying to know that Haskell’s type system can be (ab)used in this way. Check it out if you don’t like the fact that it’s hard to tell if you caught all the exceptions you care about.
The Failure typeclass is a really simple library that attempts to solve the interoperability problem by making it easy to wrap and unwrap third-party errors. I’ve used it a little, but not enough to have any authoritative opinion on the matter. It’s also worth taking a look at the Haskellwiki page.
There are two domains of error handling that you need to consider: pure errors and IO errors. For IO errors, there is a very clear winner: the mechanisms specified in Control.Exception. Use it if the error is obviously due to an imperfection in the outside universe. For pure errors, a bit more taste is necessary. Maybe should be used if there is one and only one failure case (and maybe it isn’t even that big of a deal), error may be used if it encodes an impossible condition, string errors may be OK in small applications that don’t need to react to errors, custom error types in those that do. For interoperability problems, you can easily accomodate them with your custom error type, or you can try using some of the frameworks that other people are building: maybe one will some day gain critical mass.
It should be clear that there is a great deal of choice for Haskell error reporting. However, I don’t think this choice is unjustified: each tool has situations which are appropriate for its use, and one joy of working in a high level language is that error conversion is, no really, not that hard.
August 23, 2011Consider the following data type in Haskell:
data Box a = B a
How many computable functions of type Box a -> Box a are there? If we strictly use denotational semantics, there are seven:

But if we furthermore distinguish the source of the bottom (a very operational notion), some functions with the same denotation have more implementations…
- Irrefutable pattern match:
f ~(B x) = B x. No extras. - Identity:
f b = b. No extras. - Strict:
f (B !x) = B x. No extras. - Constant boxed bottom: Three possibilities:
f _ = B (error "1"); f b = B (case b of B _ -> error "2"); and f b = B (case b of B !x -> error "3"). - Absent: Two possibilities:
f (B _) = B (error "4"); and f (B x) = B (x `seq` error "5"). - Strict constant boxed bottom:
f (B !x) = B (error "6"). - Bottom: Three possibilities:
f _ = error "7"; f (B _) = error "8"; and f (B !x) = error "9".
List was ordered by colors of the rainbow. If this was hieroglyphics to you, may I interest you in this blog post?
Postscript. GHC can and will optimize f b = B (case b of B !x -> error "3"), f (B x) = B (x `seq` error "5") and f (B !x) = error "9" into alternative forms, because in general we don’t say if seq (error "1") (error "2") is semantically equivalent error "1" or error "2": any one is possible due to imprecise exceptions. But if you really care, you can use pseq. However, even with exception set semantics, there are more functions in this “refined” view of the normal denotational semantics.
August 14, 2011This is an edited version of an email I sent last week. Unfortunately, it does require you to be familiar with the original Paxos correctness proof, so I haven’t even tried to expand it into something appropriate for a lay audience. The algorithm is probably too simple to be in the literature, except maybe informally mentioned—however, if it is wrong, I would love to know, since real code depends on it.
I would like to describe an algorithm for Paxos crash-recovery that does not require persistent storage, by utilizing synchronized clocks and a lattice-based epoch numbering. The basic idea is to increase the ballot/proposal number to one for which it is impossible for the crashed node to have made any promises for it. Such an algorithm, as noted in Paxos made Live, is useful in the case of disk corruption, where persistent storage is lost. (Unfortunately, the algorithm they describe in the paper for recovering from this situation is incorrect. The reason is left as an exercise for the reader.) It is inspired by Renesse’s remark about an “epoch-based system”, and the epoch-based crash-recovery algorithm described in JPaxos: State Machine Replication Based on the Paxos Protocol. However, in correspondence with Nuno, I discovered that proofs for the correctness of their algorithm had not been published, so I took it upon myself to convince myself of its correctness, and in the process discovered a simpler version. It may be the case that this algorithm is already in the community folklore, in which case all the better, since my primary interest is implementation.
First, let’s extend proposal numbers from a single, namespaced value n to a tuple (e, n), where n is a namespaced proposal number as before, and e is an epoch vector, with length equal to the number of nodes in the Paxos cluster, and the usual Cartesian product lattice structure imposed upon it.
Let’s establish what behavior we’d like from a node during a crash:
KNOWN-UNKNOWNS. An acceptor knows a value e*, for which for all e where e* ≤ e (using lattice ordering), the acceptor knows if it has responded to prepare requests of form (e, n) (for all n).
That is to say, the acceptor knows what set of proposal numbers he is guaranteed not to have made any promises for.
How can we establish this invariant? We might write a value to persistent storage, and then incrementing it upon a crash; this behavior is then established by monotonicity. It turns out we have other convenient sources of monotonic numbers: synchronized clocks (which are useful for Paxos in other contexts) have this behavior. So instead of using a vector of integers, we use a vector of timestamps. Upon a crash, a process sets its epoch to be the zero vector, except for its own entry, which is set to his current timestamp.
In Paxos made Simple, Lamport presents the following invariant on the operation of acceptors:
P1a. An acceptor can accept proposal numbered n iff it has not responded to a prepare request greater than n.
We can modify this invariant to the following:
P1b. An acceptor can accept proposal numbered (e, n) iff e* ≤ e and it has not responded to a prepare request (_, n') with n' > n.
Notice that this invariant “strengthens” P1a in the sense that an acceptor accepts a proposal in strictly less cases (namely, it refuses proposals when e* ≰ e). Thus, safety is preserved, but progress is now suspect.
When establishing progress of Paxos, we require that there exist a stable leader, and that this leader eventually pick a proposal number that is “high enough”. So the question is, can the leader eventually pick a proposal number that is “high enough”? Yes, define this number to be (lub{e}, max{n} + 1). Does this epoch violate KNOWN-UNKNOWNS? No, as a zero vector with a single later timestamp for that node is always incomparable with any epoch the existing system may have converged upon.
Thus, the modifications to the Paxos algorithm are as follows:
- Extend ballot numbers to include epoch numbers;
- On initial startup, set
e* to be the zero vector, with the current timestamp in this node’s entry; - Additionally reject accept requests whose epoch numbers are not greater-than or equal to
e*; - When selecting a new proposal number to propose, take the least upper bound of all epoch numbers.
An optimization is on non-crash start, initialize e* to be just the zero vector; this eliminates the need to establish an epoch in the first round of prepare requests. Cloning state from a snapshot is an orthogonal problem, and can be addressed using the same mechanisms that fix lagging replicas. We recommend also implementing the optimization in which a leader only send accept messages to a known good quorum, so a recovered node does not immediately force a view change.
I would be remiss if I did not mention some prior work in this area. In particular, in Failure Detection and Consensus in the Crash-Recovery Model, the authors present a remarkable algorithm that, without stable storage, can handle more than the majority of nodes failing simultaneously (under some conditions, which you can find in the paper). Unfortunately, their solution is dramatically more complicated than solution I have described above, and I do not know of any implementations of it. Additionally, an alternate mechanism for handling crashed nodes with no memory is a group membership mechanism. However, group membership is notoriously subtle to implement correctly.
August 5, 2011During my time at Jane Street, I’ve done a fair bit of programming involving modules. I’ve touched functors, type and module constraints, modules in modules, even first class modules (though only peripherally). Unfortunately, the chapter on modules in Advanced Topics in Types and Programming Languages made my eyes glaze over, so I can’t really call myself knowledgeable in module systems yet, but I think I have used them enough to have a few remarks about them. (All remarks about convention should be taken to be indicative of Jane Street style. Note: they’ve open sourced a bit of their software, if you actually want to look at some of the stuff I’m talking about.)
The good news is that they basically work the way you expect them to. In fact, they’re quite nifty. The most basic idiom you notice when beginning to use a codebase that uses modules a lot is you see this:
module Sexp = struct
type t = ...
...
end
There is in fact a place where I have seen this style before: Henning Thielemann’s code on Hackage, in particular data-accessor, which I have covered previously. Unlike in Haskell, this style actually makes sense in OCaml, because you never include Sexp (an unqualified import in Haskell lingo) in the conventional sense, you usually refer to the type as Sexp.t. So the basic unit of abstraction can be thought of as a type—and most simple modules are exactly this—but you can auxiliary types and functions that operate on that type. This is pretty simple to understand, and you can mostly parse the module system as a convenient namespacing mechanism.
Then things get fun.
When you use Haskell type classes, each function individually specifies what constraints on the argument there are. OCaml doesn’t have any type classes, so if you want to do that, you have to manually pass the dictionary to a function. You can do that, but it’s annoying, and OCaml programmers think bigger. So instead of passing a dictionary to a function, you pass a module to a functor, and you specialize all of your “generic” functions at once. It’s more powerful, and this power gets over the annoyance of having to explicitly specify what module your using at any given time. Constraints and modules-in-modules fall out naturally from this basic idea, when you actually try to use the module system in practice.
Probably the hardest thing (for me) to understand about the module system is how type inference and checking operate over it. Part of this is the impedance mismatch with how type classes work. When I have a function:
f :: Monoid m => m -> Int -> m
m is a polymorphic value that can get unified with any specific type. So if I do f 5 + 2, that’s completely fair game if I have an appropriate Monoid instance defined for Int (even though + is not a Monoid instance method.)
However, if I do the same trick with modules, I have to be careful about adding extra type constraints to teach the compiler that some types are, indeed, the same. Here is an example of an extra type restriction that feels like it should get unified away, but doesn’t:
module type SIG = sig
type t
val t_of_string : string -> t
end
module N : SIG = struct
type t = string
let t_of_string x = x
end
let () = print_endline (N.t_of_string "foo")
Actually, you have to specify that t and string are the same when you add that SIG declaration:
module N : SIG with type t = string = struct
Funny! (Actually, it gets more annoying when you’re specifying constraints for large amounts of types, not just one.) It’s also tricky to get right when functors are involved, and there were some bugs in pre-3.12 OCaml which meant that you had to do some ugly things to ensure you could actually write the type constraints you wanted (with type t = t… those ts are different…)
There are some times, however, when you feel like you would really, really like typeclasses in OCaml. Heavily polymorphic functionality tends to be the big one: if you have something like Sexpable (types that can be converted into S-expressions), using the module system feels very much like duck typing: if it has a sexp_of_t function, and it’s typed right, it’s “sexpable.” Goodness, most of the hairy functors in our base library are because we need to handle the moral equivalent of multiparameter type classes.
Monadic bind is, of course, hopeless. Well, it works OK if you’re only using one monad in your program (then you just specialize your >>= to that module’s implementation by opening the module). But in most applications you’re usually in one specific monad, and if you want to quickly drop into the option monad you’re out of luck. Or you could redefine the operator to be >>=~ and hope no one stabs you. :-)
August 3, 2011Hac Phi was quite productive (since I managed to get two blog posts out of it!) On Saturday I committed a new module GHC.Stats to base which implemented a modified subset of the API I proposed previously. Here is the API; to use it you’ll need to compile GHC from Git. Please test and let me know if things should get changed or clarified!
-- | Global garbage collection and memory statistics.
data GCStats = GCStats
{ bytes_allocated :: Int64 -- ^ Total number of bytes allocated
, num_gcs :: Int64 -- ^ Number of garbage collections performed
, max_bytes_used :: Int64 -- ^ Maximum number of live bytes seen so far
, num_byte_usage_samples :: Int64 -- ^ Number of byte usage samples taken
-- | Sum of all byte usage samples, can be used with
-- 'num_byte_usage_samples' to calculate averages with
-- arbitrary weighting (if you are sampling this record multiple
-- times).
, cumulative_bytes_used :: Int64
, bytes_copied :: Int64 -- ^ Number of bytes copied during GC
, current_bytes_used :: Int64 -- ^ Current number of live bytes
, current_bytes_slop :: Int64 -- ^ Current number of bytes lost to slop
, max_bytes_slop :: Int64 -- ^ Maximum number of bytes lost to slop at any one time so far
, peak_megabytes_allocated :: Int64 -- ^ Maximum number of megabytes allocated
-- | CPU time spent running mutator threads. This does not include
-- any profiling overhead or initialization.
, mutator_cpu_seconds :: Double
-- | Wall clock time spent running mutator threads. This does not
-- include initialization.
, mutator_wall_seconds :: Double
, gc_cpu_seconds :: Double -- ^ CPU time spent running GC
, gc_wall_seconds :: Double -- ^ Wall clock time spent running GC
-- | Number of bytes copied during GC, minus space held by mutable
-- lists held by the capabilities. Can be used with
-- 'par_max_bytes_copied' to determine how well parallel GC utilized
-- all cores.
, par_avg_bytes_copied :: Int64
-- | Sum of number of bytes copied each GC by the most active GC
-- thread each GC. The ratio of 'par_avg_bytes_copied' divided by
-- 'par_max_bytes_copied' approaches 1 for a maximally sequential
-- run and approaches the number of threads (set by the RTS flag
-- @-N@) for a maximally parallel run.
, par_max_bytes_copied :: Int64
} deriving (Show, Read)
-- | Retrieves garbage collection and memory statistics as of the last
-- garbage collection. If you would like your statistics as recent as
-- possible, first run a 'performGC' from "System.Mem".
getGCStats :: IO GCStats
August 1, 2011As it stands, it is impossible to define certain value-strict operations on IntMaps with the current containers API. The reader is invited, for example, to try efficiently implementing map :: (a -> b) -> IntMap a -> IntMap b, in such a way that for a non-bottom and non-empty map m, Data.IntMap.map (\_ -> undefined) m == undefined.
Now, we could have just added a lot of apostrophe suffixed operations to the existing API, which would have greatly blown it up in size, but following conversation on libraries@haskell.org, we’ve decided we will be splitting up the module into two modules: Data.IntMap.Strict and Data.IntMap.Lazy. For backwards compatibility, Data.IntMap will be the lazy version of the module, and the current value-strict functions residing in this module will be deprecated.
The details of what happened are a little subtle. Here is the reader’s digest version:
- The
IntMap in Data.IntMap.Strict and the IntMap in Data.IntMap.Lazy are exactly the same map; there is no runtime or type level difference between the two. The user can swap between “implementations” by importing one module or another, but we won’t prevent you from using lazy functions on strict maps. You can convert lazy maps to strict ones using seqFoldable. - Similarly, if you pass a map with lazy values to a strict function, the function will do the maximally lazy operation on the map that would still result in correct operation in the strict case. Usually, this means that the lazy value probably won’t get evaluated… unless it is.
- Most type class instances remain valid for both strict and lazy maps, however,
Functor and Traversable do not have valid “strict” versions which obey the appropriate laws, so we’ve selected the lazy implementation for them. - The lazy and strict folds remain, because whether or not a fold is strict is independent of whether or not the data structure is value strict or spine strict.
I hacked up a first version for the strict module at Hac Phi on Sunday, you can see it here. The full implementation can be found here.
July 29, 2011Fall is coming, and with it come hoards of ravenous Freshmen arriving on MIT’s campus. I’ll be doing three food events… all of them functional programming puns. Whee!
Anamorphism: the building up of a structure. Catamorphism: the consumption of a structure. Hylomorphism: both an anamorphism and a catamorphism. This event? A hylomorphism on dumplings. Come learn the basic fold, or just perform a metabolic reduction on food.
I’ve done this event several times in the past and it’s always good (if a little sweaty) fun. Dumpling making, as it turns out, is an extremely parallelizable task: you can have multiple people rolling out wraps, wrapping the dumplings, and a few brave cooks actually boiling or pan-frying them. (Actually, in China, no one makes their own wraps anymore, because the store bought ones are so good. Not so in the US…)
The combinator is familiar to computer scientists, but less well known to food scientists. A closely guarded secret among the Chinese is the WOK combinator, guaranteed to combine vegetable and meat in record runtime. (Vegan-friendly too.)
Dumplings are a little impractical for an MIT student in the thick of term; they usually tend to get reserved for special events near the beginning of term, if at all. However, stir fry is quick, cheap and easy and an essential healthy component to any college student’s diet. My personal mainstay is broccoli and chicken (which is nearly impossible to get wrong), but I’ve diversified and I’m quite a fan of bell peppers and chorizo these days too (see below). One difficulty with running this event is making sure there are enough rice cookers… running out of rice is no fun, since it takes so long to cook up a new batch!
Roast(X) where X = {Broccoli, Garlic, Pork, Bell Peppers, Chorizo, Carrots, Onions, Asparagus, Sweet Potatoes}.
This is a new one. Really, I just wanted to do roast broccoli with garlic. It’s sooooo good. I’ve never roasted chorizo before, but there didn’t seem to be enough meat on the menu, so I tossed it in. I did a lot of roasting when I was in Portland, because I’d frequently buy random vegetables at the farmers markets, get home, and then have to figure out how to cook them. Roasting is a pretty good bet, in many cases! I forgot to put beets in the event description; maybe I’ll get some…
July 27, 2011This post was adapted from a post I made to the glasgow-haskell-users list.
According to Control.Exception, the BlockedIndefinitelyOnMVar exception (and related exception BlockedIndefinitelyOnSTM) is thrown when “the thread is blocked on an MVar, but there are no other references to the MVar so it can’t ever continue.” The description is actually reasonably precise, but it is easy to misinterpret. Fully understanding how this exception works requires some extra documentation from Control.Concurrent as well as an intuitive feel for how garbage collection in GHC works with respects to Haskell’s green threads.
Here’s the litmus test: can you predict what these three programs will do? :
main1 = do
lock <- newMVar ()
forkIO $ takeMVar lock
forkIO $ takeMVar lock
threadDelay 1000 -- let threads run
performGC -- trigger exception
threadDelay 1000
main2 = do
lock <- newEmptyMVar
complete <- newEmptyMVar
forkIO $ takeMVar lock `finally` putMVar complete ()
takeMVar complete
main3 = do
lock <- newEmptyMVar
forkIO $ takeMVar lock `finally` putMVar lock ()
let loop = do
b <- isEmptyMVar lock
if b
then yield >> performGC >> loop
else return ()
loop
Try not to peek. For a hint, check the documentation for forkIO.
The first program gives no output, even though the threadDelay ostensibly lets both forked threads get scheduled, run, and deadlocked. In fact, BlockedIndefinitelyOnMVar is raised, and the reason you don’t see it is because forkIO installs an exception handler that mutes this exception, along with BlockedIndefinitelyOnSTM and ThreadKilled. You can install your own exception handler using catch and co.
There is an interesting extra set of incants at the end of this program that ensure, with high probability, that the threads get scheduled and the BlockedIndefinitelyOnMVar exception gets thrown. Notice that the exception only gets thrown when “no references are left to the MVar.” Since Haskell is a garbage collected language, the only time it finds out references are gone are when garbage collections happen, so you need to make sure one of those occurs before you see one of these errors.
One implication of this is that GHC does not magically know which thread to throw the exception at to “unwedge” the program: instead, it will just throw BlockedIndefinitelyOnMVar at all of the deadlocked threads, including (if applicable) the main thread. This behavior is demonstrated in the second program, where the program terminates with BlockedIndefinitelyOnMVar because the main thread gets a copy of the exception, even though the finally handler of the child thread would have resolved the deadlock. Try replacing the last line with takeMVar complete `catch` \BlockedIndefinitelyOnMVar -> takeMVar complete >> putStrLn "done". It’s pretty hilarious.
The last program considers what it means for an MVar to be “reachable”. As it deadlocks silently, this must mean the MVar stayed reachable; and indeed, our reference isEmptyMVar prevents the MVar from ever going dead, and thus we loop infinitely, even though there was no possibility of the MVar getting filled in. GHC only knows that a thread can be considered garbage (which results in the exception being thrown) if there are no references to it. Who is holding a reference to the thread? The MVar, as the thread is blocking on this data structure and has added itself to the blocking list of this. Who is keeping the MVar alive? Why, our closure that contains a call to isEmptyMVar. So the thread stays. The general rule is as follows: if a thread is blocked on an MVar which is accessible from a non-blocked thread, the thread sticks around. While there are some obvious cases (which GHC doesn’t manage) where the MVar is obviously dead, even if there are references sticking around to it, figuring this out in general is undecidable. (Exercise: Write a program that solves the halting problem if GHC was able to figure this out in general.)
To conclude, without a bit of work (which would be, by the way, quite interesting to see), BlockedIndefinitelyOnMVar is not an obviously useful mechanism for giving your Haskell programs deadlock protection. Instead, you are invited to think of it as a way of garbage collecting threads that would have otherwise languished around forever: by default, a deadlocked thread is silent (except in memory usage.) The fact that an exception shows up was convenient, operationally speaking, but should not be relied on.