May 16, 2012“…so that’s what we’re going to build!”
“Cool! What language are you going to write it in?”
“Well, we were thinking we were going to need three programming languages…”
“…three?”
“…and they’ll be research programming languages too…”
“Are you out of your mind?”
This was the conversation in streaming through my head when I decided that I would be writing my latest software project in Coq, Haskell and Ur/Web. I had reasonably good reasons for the choice: I wanted Coq because I didn’t actually want to implement a theorem prover from scratch, I wanted Ur/Web because I didn’t actually want to hand write JavaScript to get an AJAX interface, and I wanted Haskell because I didn’t want to write a bucket of C to get Ur/Web and Coq to talk to each other. But taken altogether the whole thing seemed a bit ludicrous, like an unholy fusion of a trinity of research programming languages.
In the end, it worked out quite well. Now, what this means depends on your expectations: it was not the case that “everything worked out of the box and had very nice instructions attached.” However, if it was the case that:
- No single issue ended up requiring an unbounded amount of time and yak shaving,
- Any patches written made it into upstream, improving the situation of the software for future developers, and
- The time spent on engineering grease is less than the time it would have taken to build the system with inferior languages,
- Everyone involved in the project is willing to learn all of the languages involved (easy if it’s only one person),
then yes, it worked “quite well”. In this post, I’d like to describe in a little more detail what happened when I put these three languages together and speculate wildly about general maxims that might apply when someone is doing something similar.
While Coq is a research language, it is also in very wide use among academics, and most of its instability lies in advanced features that I did not use in my project. So the primary issues I encountered with Coq were not bugs, but in integrating it with the system (namely, making it talk to Haskell).
Maxim 1. Interchange formats will be undocumented and just good enough to get the job done.
Coq is already designed to allow for communication between processes (this is how the Proof General/Emacs and Coq talk to each other), but the format between coqtop and Proof General was undocumented, ad hoc, and didn’t transmit enough information for my application. In the face of such a situation, there are two ways to proceed: grit your teeth and implement the bad protocol or patch the compiler to make a better one. I chose the latter, and learned something very interesting:
Maxim 2. In ML-like languages, it’s very easy to make simple but far reaching changes to a codebase, due to the assistance of the typechecker.
Making the changes to the frontend was very simple; there was nothing deep about the change, and a combination of the typechecker and grep allowed me to pull off the patch with zero debugging. With a few XML tags at a few key spots, I got output reasonable enough to build the rest of the system with.
Aside. Later, I learned that coqide in recent versions of Coq (8.4 and later) has another interchange format. Moving forward, it is probably the correct mechanism to interact with Coq interactively, though this is made somewhat more difficult by the fact that the interchange format is undocumented; however, I’ve filed a bug. With any luck, it will hopefully do better than my patch. My patch was originally intended to be a partial implementation of PGIP, a generic interchange format for interacting with theorem provers, but the Coq developers and I later discovered that the PGIP project is inactive, and the other user, Isabelle, has discontinued using their PGIP backend. (Sometimes standards don’t help!)
Ur/Web is comparatively less used, and accordingly we ran into a variety of bugs and other infelicities spanning all parts of the system, from the frontend to the compiler. Were they blockers? No!
Maxim 3. A deterministically reproducible bug in some core functionality will get fixed very quickly by an active original author of the code.
This maxim doesn’t apply to fundamental limitations in design (where the fix will take a lot of elbow grease, though the author will usually have a good idea when that’s the case), but other bugs of this type, I found I could get freakishly quick turnaround times for fixes. While I may attribute part of this to the fact that my advisor was the one who wrote the compiler, I don’t think that’s all there is to it. There is a certain pride that comes with an interesting, tricky bit of code you wrote, that makes it an irresistible little puzzle when someone shows you a bug. And we love little puzzles.
There’s also a corollary:
Maxim 4. The less interesting a problem is to the academic, the more likely it is you’ll be able to fix it yourself.
Academics are somewhat allergic to problems that they’re not interested in and which aren’t vital for their research. This means they don’t like working on these bits, but it also means that they’ve probably kept it simple, which means you’re more likely to be able to figure it out. (A good typechecker also really helps! See maxim 2.) There was a simple bug with serving 404s from FastCGI’s compiled by Ur/Web, which had a very simple fix; I also made some modifications to Ur/Web made it runnable without having to make install first. Maintainers of active research software tend to be quite receptive to these “engineering” patches, which serve no direct research purpose. I consider these contributes to be a vital component of being a good citizen of the open source community.
OK, Haskell is not really “just” a research language anymore; it is also a very flexible general purpose language which has seen quite a bit of real world use and can be treated as an “ordinary” language in that respect. This made it a good choice for gluing the two other languages together; it can do just about anything, and has very good FFI support for calling into and out of Haskell. This brings us to our next maxim:
Maxim 5. An FFI is a crucial feature for any DSL, and should be a top priority among tasks involved in preparing a language for general usage.
Having Haskell and Ur/Web talk to each other through their FFIs was key for making this all work. Ur/Web is a domain specific language for writing web applications, and among other things it does not include robust systems libraries (e.g. executing external processes and interfacing with them). Most languages will have this problem, since library support takes a bit of work to add, but Ur/Web has a second problem: all side-effectful transactions need to also be able to be rolled back, and this is rather hard to achieve for general input-output. However, with an FFI, we can implement any code which needs this library support in a more suitable language (Haskell), wrap it up in an API which gives the appropriate transactional guarantees, and let Ur/Web use it. Without it, we would not have been able to use Ur/Web: it’s an extremely flexible escape hatch.
Specifying an FFI also is a good way of demonstrating how your language is different from C: it forces you to think about what invariants you expect foreign functions to have (referential transparency? thread-safety?): these invariants are exactly the ones that get automatically fulfilled by code written in your language. That’s pretty cool!
However, because functions which manipulate C pointers are non-transactional, Ur/Web is limited to FFI functions which handle basic C types, e.g. integers and strings. Thus the question of parsing becomes one of utmost importance for Ur/Web, as strings are the preferred interchange format for complex structures. While different languages will have different situations, in general:
Maxim 6. Make sure you know how to do parsing in all of the languages involved.
I’ve presented six maxims of research polyglottism:
- Interchange formats will be undocumented and just good enough to get the job done.
- In ML-like languages, it’s very easy to make simple but far reaching changes to a codebase, due to the assistance of the typechecker.
- A deterministically reproducible bug in some core functionality will get fixed very quickly by an active original author of the code.
- The less interesting a problem is to the academic, the more likely it is you’ll be able to fix it yourself.
- An FFI is a crucial feature for any DSL, and should be a top priority among tasks involved in preparing a language for general usage.
- Make sure you know how to do parsing in all of the languages involved.
If you keep all of these maxims in mind, I believe that the tradeoff between some extra bugfixing and yak shaving for the benefits of the research programming language is a compelling one, and one that should be considered seriously. Yes, you have to be willing to muck around with the innards of all the tools you use, but for any sufficiently important tool, this is inevitably true. And what is a more important tool than your compiler?
Postscript. The application in question is Logitext.
May 13, 2012While working on my senior thesis, I had to write a prior work section, which ended up being a minisurvey for the particular subfield my topic was in. In the process, a little bird told me some things…
- If you can, ask someone who might know a little bit about the subject to give you the rundown: there’s a lot of knowledge in people’s heads which never got written down. But also be aware that they will probably have their blind spots.
- It is better to do the literature review later rather than earlier, after you have started digging into the topic. I have been told if you read the literature too early, you will get spoiled and stop thinking novel thoughts. But I also think there is also a little bit of “you’ll understand the literature better” if you’ve already thought about the topic on your own. Plus, it’s easy to think that everything has been done before: it’s simply not true! (But if you think this, you will get needlessly discouraged.)
- Don’t indiscriminately add papers to your database. You should have something you want to do with it: is it an important paper that you have to cite because everyone knows about it? Is it directly addressing the issue you’re dealing with? Does it happen to be particularly well written? Is it something that you could see yourself reading more carefully later? Don’t be afraid to toss the paper out; if it actually was important, you’ll run into it again later.
- Every researcher is a historian. When you look at a paper, you’re not just looking at what is written inside it, but its social context. There’s a reason why “prior work” is so important to academics. If you don’t understand a paper’s context, it’s unlikely you’ll understand the paper.
- Researchers don’t necessarily talk to each other. Pay attention to who they cite; it says a little bit about what community they’re in.
- Researchers are happy to send you copies of papers they have written (so fear not the paywall that your university hasn’t subscribed to). They may even volunteer extra information which may come in handy.
- Be methodical. You’re doing a search, and this means carefully noting down which papers you skimmed, and what you got out of them, and keeping track of other veins of research that you need to follow up on. It’s like chasing a rabbit down a hole, but if you have some clearly defined search criteria, eventually you’ll bottom out. You can prune the uninteresting papers later; the point here is to avoid duplicating work.
- Read papers critically. Not everything that is published is good; that’s the point of research!
What are your favorite maxims to keep in mind while you’re surveying the literature?
April 20, 2012Ur is a programming language, which among other things, has a rather interesting record system. Record systems are a topic of rather intense debate in the Haskell community, and I noticed that someone had remarked “[Ur/Web has a http://www.impredicative.com/ur/tutorial/tlc.html very advanced records system]. If someone could look at the UR implementation paper and attempt to distill a records explanation to a Haskell point of view that would be very helpful!” This post attempts to perform that distillation, based off my experiences interacting with the Ur record system and one of its primary reasons for existence: metaprogramming. (Minor nomenclature note: Ur is the base language, while Ur/Web is a specialization of the base language for web programming, that also happens to actually have a compiler. For the sake of technical precision, I will refer to the language as Ur throughout this article.)
In Haskell, if you want to define a record, you have to go and write out a data declaration:
data Foo = Foo { bar :: Int, baz :: Bool }
In Ur, these two concepts are separate: you can define an algebraic data type (the Foo constructor) and you can write types which describe a record (the { foo :: Int, bar :: Bool} bit of the type). To emphasize this point, there are actually a lot of ways I can spell this record in Ur/Web. I can define a type synonym:
type foo = { Bar : int, Baz : bool }
which offers me no protection from mixing it up with a structurally similar but semantically different type qux = { Bar : int, Baz : bool }, or I can define:
datatype foo = Foo of { Bar : int, Baz : bool }
which desugars into:
type foo' = { Bar : int, Baz : bool }
datatype foo = Foo of foo'
that is to say, the datatype has a single constructor, which takes only one argument, which is a record! This definition is closer to the spirit of the original Haskell definition. (ML users might be familiar with this style; Ur definitely comes from that lineage.)
This design of separating algebraic data types from records means we now have obvious facilities for record construction (let val x = { Bar = 2, Baz = true }) and record projection (x.Bar); though if I have a datatype I have to unwrap it before I can project from it. These record types are unique up to permutation (order doesn’t matter), which makes them a bit more interesting than HList. They are also nicely parsimonious: unit is just the empty record type {}, and tuples are just records with special field names: 1, 2, etc.
Now, if this was all there was to the Ur record system, it wouldn’t be very interesting. But actually, the field #Bar is a first class expression in the language, and the curly brace record type syntax is actually syntax sugar! Unpacking this will require us to define quite a few new kinds, as well as a lot of type level computation.
In vanilla Haskell, we have only one kind: *, which in Ur parlance is a Type. Values inhabit types which inhabit this kind. Ur’s record system, however, demands more exotic kinds: one such kind is the Name kind, which represents a record field name (#Foo is one). However, GHC has this already: it is the recently added Symbol kind. What GHC doesn’t have, however, is the kind constructor {k}, which is the kind of a “type-level record.” If value-level records are things that contain data, type-level records are the things that describe value-level records. They are not, however, the type of the value-level records (because if they were, their kind would be Type). Let’s look at a concrete example.
When I write:
type foo = { Bar : int, Baz : bool }
What I’m really writing is:
type foo = $[ Bar = int, Baz = bool ]
The $ is a type level operator, being applied to the expression [ Bar = int, Baz = bool ], which is a type level record, specifically of kind {Type} (the “values” of the record are types). The dollar sign takes type level records, and transforms them into Type (so that they can actually be inhabited by values).
This may seem like a meaningless distinction, until you realize that Ur has type level operators which work only on type level records, and not types in general. The two most important primitive type level operations are concatenation and map. They both do what you might expect: concatenation takes two records and puts them together, and map takes a type level function and applies it to every member of the record: so I can easily transform [ Bar = int, Baz = bool ] into [ Bar = list int, Baz = list bool ] by mapping the list type constructor. Extensible records and metaprogramming dispatched in one swoop!
Now, recall that field names all live in a global namespace. So what happens if I attempt to do [ Bar = bool ] ++ [ Bar = int ]? The Ur type checker will reject this statement as ill-typed, because I have not provided the (unsatisfiable) proof obligation that these records are disjoint. In general, if I have two record types t1 and t2 which I would like to concatenate, I need a disjointness proof [t1 ~ t2]. Handling disjointness proofs feels rather unusual to users coming from traditional functional programming languages, but not all that odd for users of dependently typed languages. In fact, the Ur/Web compiler makes handling disjointness obligations very easy, automatically inferring them for you if possible and knowing some basic facts about about concatenate and map.
The Ur record system crucially relies on type level computation for its expressiveness: we can expand, shrink and map over records, and we can also take advantage of “folders”, which are functions which use the type level records as structure to allow generic folding over records. For more information about these, I suggest consulting the type level computation tutorial. But in order to offer these features in a user friendly way, Ur crucially relies on a compiler which has some level of knowledge of how these operators work, in order to avoid making users discharge lots of trivial proof obligations.
Unfortunately, here I must admit ignorance as to how the rest of the Haskell record proposals work, as well as how a record system like this would interact with Haskell (Ur does have typeclasses, so this interaction is at least reasonably well studied.) While this proposal has the benefit of having a well specified system in an existing language, it is complex, and definitely shooting for the moon. But I think it says a bit about what might have to be added, beyond type-level strings, to fulfill Gershom Bazerman’s vision here:
It seems to me that there’s only one essential missing language feature, which is appropriately-kinded type-level strings (and, ideally, the ability to reflect these strings back down to the value level). Given that, template haskell, and the HList bag of tricks, I’m confident that a fair number of elegant records packages can be crafted. Based on that experience, we can then decide what syntactic sugar would be useful to elide the TH layer altogether.
April 17, 2012
March 24, 2012This is a very quick and easy fix that has made latency on Ubuntu servers I maintain go from three to four seconds to instantaneous. If you’ve noticed that you have high latency on ssh or scp (or even other software like remctl), and you have control over your server, try this on the server: aptitude remove libnss-mdns. It turns out that multicast DNS on Ubuntu has a longstanding bug on Ubuntu where they didn’t correctly tune the timeouts, which results in extremely bad performance on reverse DNS lookups when an IP has no name.
Removing multicast DNS will break some applications which rely on multicast DNS; however, if you’re running Linux you probably won’t notice. There are a number of other solutions listed on the bug I linked above which you’re also welcome to try.
March 20, 2012If you haven’t noticed, these are coming in the order of the visit days.
Whereas the weather at UPenn was nice and sunny, the NJ Transit dinghy rolled into a very misty Princeton. Fortunately, I had properly registered for this visit day, so the hotel was in order. I was a bit early, so I met up with an old friend who had recently penned this short story and we talked about various bits and bobs (“I hear you’re up for a Hugo!”) before I meandered over to the computer science building.
The Princeton campus also holds some distinctive memories for me, a patchwork of experiences of my high school self, including a unpleasant month temping for the Princeton Wind Ensemble (I’ve been since informed that the ensemble is much healthier now), visits to the area for various reasons, a fascinating interview in which I was told that “I should not go to Princeton”, and a very pleasant, if slightly out-of-place, campus preview weekend. Of course, it is the case that graduate student life is completely different from undergraduate life, so I was prepared to shelve these experiences for my second visit.
One of the most interesting things I realized about Princeton computer science, during Andrew Appel’s speech during the admit’s reception dinner, was how many famous computer scientists had graded Princeton with their presence at some point or another; these included Church, Turing, Gödel, Neumann, and others… One of the insights of his talk was this: “maybe your PhD thesis doesn’t need to be your most important work, but maybe you can have a four page aside which sets forth one of the most important techniques in computer science.” (He was referring to Alan Turing’s thesis, in which he introduced the concept of relative computing.)
Some “facts”: at Princeton, your advisors work to get you out, so you don’t have to worry about dallying too long on the PhD. Being a part-time student is not ok, and Princeton does have qualifying exams, but you’ll probably pass. (The overall wisdom that I came away with here is that computer science quals are very different from quals in other PhD disciplines, where the qual is very much a weeder. In CS, they want you to pass.) The generals are in some sense a checkpoint, where you can figure out whether or not you’re happy with the research you’re doing with your advisor. You need to take six classes, four in distribution, but you can pass out of the final. You spend your second year teaching, both semesters as a “preceptor”. You pick your advisor at the end of your first year, and five people serve on your thesis committee (it tends not to be too adversarial). You’re relatively shielded from grants.
Andrew Appel is a very smart man. He’s been recently working with my current advisor Adam Chlipala, and their research interests have some overlap. He is working on a verified software toolchain, but he’s also happy to tackle smaller problems. One of the small theoretical problems he showed us during our three-on-one meeting was the problem of calculating fixpoints of functions which are not monotonic, but instead oscillate towards some convergence (this occurs when the recursion shows up in the contravariant position; as strange as this may seem, this shows up a bit in object oriented languages!) One of his grad students told me he likes “semantic definitions”, and is not afraid to take on large challenges or tackle the gritty details of languages like Cminor, integer alignment, or scaling up theoretical techniques for large programs. And despite being department chair, it’s easy to schedule time with him, and he seems to have this uncanny ability to generate grants.
David Walker is very excited about the Frenetic programming language, which is a language for dealing with network programming. I already had a bit of context about this, because Jennifer Rexford had given an invited talk at POPL about this topic. One of the interesting things I noticed when hearing about OpenFlow for the second time was how similar its handling of unknown events was to hardware: if the efficient lookup table doesn’t know what to do, you interrupt and go to a slow, general purpose computer, which figures out what to do, installs the rule in the lookup table, and sends the packet on its way. The three of us might have been a technical mood, because we ended up asking him to give us the gory details of per-packet consistency when updating network rules. I hear in another life David Walker also did type systems, and has also done a bit of work in semantics. One contrast a grad student noted between Appel and Walker was that Appel would assume you know what he is talking about (so it’s your onus to interrupt him if you don’t: a useful skill!), whereas Walker will always go and explain everything and always stop you if he doesn’t know what you’re talking about. This makes him really good at communicating. (Oh, did I mention Frenetic is written in Haskell?)
Randomly, I discovered one of the current grad students was the creator of smogon.com. He does PL research now: but it’s kind of nifty to see how interests change over the years…
March 18, 2012Note: this is not a discussion of Hilbert’s formalism versus Brouwer’s intuitionism; I’m using formalism and intuition in a more loose sense, where formalism represents symbols and formal systems which we use to rigorously define arguments (though not logic: a sliding scale of rigor is allowed here), while intuition represents a hand-wavy argument, the mental model mathematicians actually carry in their head.
Formalism and intuition should be taught together.
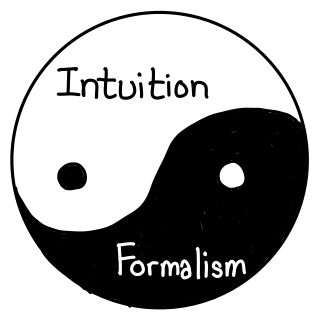
But as utterly uncontroversial as this statement may be, I think it is worth elaborating why this is the case—the reason we find will say important things about how to approach learning difficult new technical concepts.
Taken in isolation, formalism and intuition are remarkably poor teachers. Have you had the reading a mathematical textbook written in the classic style, all of the definitions crammed up at the beginning of the chapter in what seems like a formidable, almost impenetrable barrier. One thinks, “If only the author had bothered to throw us a few sentences explaining what it is we’re actually trying to do here!” But at the same time, I think that we have all also had the experience of humming along to a nice, informal description, when we really haven’t learned much at all: when we sit down and try to actually solve some problems, we find these descriptions frustratingly vague. It’s easy to conclude that there really is no royal road to intuition, that it must be hard won by climbing the mountains of formalism.
So why is the situation any different when we put them together?
The analogy I like is this: formalism is the object under study, whereas intuition is the results of such a study. Imagine an archaeologist who is attempting to explain to his colleagues a new conclusion he has drawn from a recently excavated artifact. Formalism without intuition is the equivalent of handing over the actual physical artifact without any notes. You can in principle reconstruct the conclusions, but it might take a while. Intuition without formalism, however, is the equivalent of describing your results over the phone. It conveys some information, but not with the resolution or fidelity of actually having the artifact in your hands.
This interpretation explains a bit about how I learn mathematics. For example, most mathematical formalisms aren’t artifacts you can “hold in your hand”—at least, not without a little practice. Instead, they are giant mazes, of which you may have visibility of small fragments of at a time. (The parable of the blind men and the elephant comes to mind.) Being able to hold more of the formalism in your head, at once, increases your visibility. Being able to do quick inference increases your visibility. So memorization and rote exercise do have an important part to play in learning mathematics; they increase our facility of handling the bare formalism.
However, when it comes to humans, intuition is our most powerful weapon. With it, we can guess that things are true long before we have any good reason of thinking it is the case. But it is inextricably linked to the formalism which it describes and a working intuition is no where near as easily transferable as a description of a formal system. Intuition is not something you can learn; it is something that assists you as you explore the formalism: “the map of intuition.” You still have to explore the formalism, but you shouldn’t feel bad about frequently consulting your map.
I’ve started using this idea for when I take notes in proof-oriented classes, e.g. this set of notes on the probabilistic method (PDF). The text in black is the formal proof; but interspersed throughout there are blue and red comments trying to explicate “what it is we’re doing here.” For me, these have the largest added value of anything the lecturer gives, since I find these remarks are usually nowhere to be seen in any written notes or even scribe notes. I write them down even if I have no idea what the intuition is supposed to mean (because I’ll usually figure it out later.) I’ve also decided that my ideal note-taking setup is already having all of the formalism written down, so I can pay closer attention to any off-hand remarks the lecturer may be making. (It also means, if I’m bored, I can read ahead in the lecture, rather than disengage.)
We should encourage this style of presentation in static media, and I think a crucial step towards making this possible is easier annotation. A chalkboard is a two-dimensional medium, but when we LaTeX our presentation goes one-dimensional, and we rely on the written word to do most of the heavy lifting. This is fine, but a bit of work, and it means that people don’t do it as frequently as we might like. I’m not sure what the best such system would look like (I am personally a fan of hand-written notes, but this is certainly not for everyone!), but I’m optimistic about the annotated textbooks that are coming out from the recent spate of teaching startups.
For further reading, I encourage you to look at William Thurston’s essay, On proof and progress in mathematics, which has had a great influence on my thoughts in this matter.
March 16, 2012I’m hoping that this will be the beginning of a series of posts describing all of the visit days/open houses that I attended over the past month. Most of the information is being sucked out of the notes I took during the visits, so it’s very stream of consciousness style. It’s kind of personal, and I won’t be offended if you decide not to read. You’ve been warned!
I arrive at the Inn at Penn shortly before midnight, and check in. Well, attempt it; they appear to have no reservation on hand. It appears that I hadn’t actually registered for the visit weekend. Oops.
Sam tells me later that first impressions stick, and that her first impression of me was a thoroughly discombobulated PhD admit. Ruffle up my hair! Ask if they’re a fellow CS PhD admit, whether or not they have a room, oh, and by the way, what is your name? (I didn’t realize that was the real sticking point until she told me about it at the end of the CMU visit.) But Brent is on IRC and I ping him and he knows a guy named Antal who is also visiting UPenn so I give him a call and he lends me his room for a night and things are good. (Mike, the graduate studies coordinator, is kind of enough to fit me into schedules the next day. Thank you Mike!)
I’ve been to UPenn before. I visited with my Dad; Roy Vagelos was former CEO of Merck and a large influence on UPenn, and at one point I had private aspirations of doing my undergraduate degree in something non-CS before hopping to computer science graduate school. But when the MIT and Princeton admissions came UPenn got soundly bumped off the table, and this experience was wrapped up and stowed away. But I recognized small pieces of the campus from that visit, stitched together with the more recent experience of Hac Phi and POPL. Our tour of Philadelphia lead us to the Bed and Breakfast I stayed at POPL, and I was Surprised™.
Benjamin Pierce is flying off to Sweden for WG 2.8 (a magical place of fairies, skiing and functional programming), so he’s only around for the morning presentations, but during breakfast he talks a bit about differential privacy to a few of the candidates, and then heads up the presentations. I hear from his students that he’s gotten quite involved with the CRASH project, and is looking a lot more at the hardware side of things. One of the remarkable things that I heard in the morning talks was how programming languages has sort of leaked into all of the CS research that was presented (or maybe that was just selection bias?) Well, not everyone: the machine learning researchers just “want to do a lot of math” (but maybe we still get a little worried about privacy.)
UPenn is well known for its PL group, where “we write a little bit of Greek every day.” It’s really quite impressive walking into the PL lunch, with a battalion of grad students lined up against the back wall cracking jokes about Coq and Haskell and the presentation is about F*.
Here are some “facts”. At UPenn you spend two semesters TAing, there’s an office lottery but people in the same group tend to cluster together, you don’t have to work on grants, the professors are super understanding of graduate student’s life situations, the living costs are around $500/mo, and that it is a very laid back place. Your advisor is very much in charge of your degree, except once a year when there’s a department wide review to check no one falls through the cracks. The drop-out rate is low. UPenn has a nice gym which is $400/yr. Biking Philadelphia is great, but you shouldn’t live in grad housing. Because there is a power trio of Pierce, Zdancewic and Weirich, when it comes time for you to form your thesis committee, the other two profs who aren’t your advisor serve on your committee. The PL group is in a slightly unusual situation where there aren’t any 2nd or 3rd year students (this was due to a double-sabbatical one year, and bad luck of the draw another.) But there are infinitely many 1st year students. You have to take three laid back exams. Philadelphia is a nice and large city (5th biggest!) UPenn and CMU are perhaps the biggest pure programming languages departments out of the places I visited.
Stephanie Weirich is super-interested in dependently typed languages. She wants to find out how to get functional programmers to use dependent types, and she’s attacking it from two sides: you can take a language like Haskell for which we are adding more and more features moving it towards dependent types, and you can build a language from scratch like TRELLYS which attempts to integrate dependent types in a usable way. She’s not shy about giving 1st years really hard projects, but she’s happy to do random stuff with students. She reflects on Dimitrios Vytiniotis’ trajectory: where he discovered his true calling with polymorphism and Haskell, and is now off designing crazy type systems with Simon Peyton Jones at Microsoft Research. “I can’t make you go crazy about a topic,” (in the good sense) but she’s interested in helping you find out what lights you on fire. I ask her about the technical skills involved in developing metatheory for type systems (after all, it’s very rare for an undergraduate to have any experience in this sort of thing): she tells me it’s all about seeing lots of examples, figuring out what’s going to get you in trouble. (In some sense, it’s not “deep”, although maybe any poor computer scientist who has tried to puzzle out the paper of a type theorist might disagree.)
Steve Zdancewic has a bit more spread of research interests, but one of the exciting things coming out is the fact that they have Coq infrastructure for LLVM that they’ve been working on over the course of the year, and now it’s time to use the infrastructure for cool things, such as do big proofs and figure out what’s going on. There have been a lot of cases where doing just this has lead to lots of interesting insights (including realization that many proofs were instances of a general technique): mechanized verification is a good thing. He also has some side projects, including compilers for programming languages that will execute on quantum computers (all the computations have to be reversible! There is in fact a whole conference on this; it turns out you can do things like reduce heat emissions.) There’s also a bit of interest in program synthesis. Steve echoes Stephanie when he says, “I am enthusastic about anything that my students are interested in enough to convince me to be enthusiastic about.” They don’t do the chemistry model of getting a PhD, where you “use this pipette a hundred million times.”
In the words of one grad student, these are professors that are “friendly and much smarter than you!” They’re happy to play around and have fun with programming languages concepts (as opposed to the very hard core type theory research happening at CMU; but more on that later.)
We’ll close with a picture, seen in the neighborhoods of Philadelphia.

March 5, 2012Suppose that you have k sorted arrays, each of size n. You would like to search for single element in each of the k arrays (or its predecessor, if it doesn’t exist).

Obviously you can binary search each array individually, resulting in a $O(k\lg n)$ runtime. But we might think we can do better that: after all, we’re doing the same search k times, and maybe we can “reuse” the results of the first search for later searches.
Here’s another obvious thing we can do: for every element in the first array, let’s give it a pointer to the element with the same value in the second array (or if the value doesn’t exist, the predecessor.) Then once we’ve found the item in the first array, we can just follow these pointers down in order to figure out where the item is in all the other arrays.

But there’s a problem: sometimes, these pointers won’t help us at all. In particular, if a later lists is completely “in between” two elements of the first list, we have to redo the entire search, since the pointer gave us no information that we didn’t already know.

So what do we do? Consider the case where k = 2; everything would be better if only we could guarantee that the first list contained the right elements to give you useful information about the second array. We could just merge the arrays, but if we did this in the general case we’d end up with a totally merged array of size $kn$, which is not so good if k is large.
But we don’t need all of the elements of the second array; every other item will do!

Let’s repeatedly do this. Take the last array, take every other element and merge it into the second to last array. Now, with the new second to last array, do this to the next array. Rinse and repeat. How big does the first array end up being? You can solve the recurrence: $T(k) = n + T(k-1)/2$, which is the geometric series $n + n/2 + n/4 + n/8 + \ldots = 2n$. Amazingly, the new first list is only twice as large, which is only one extra step in the binary search!

What we have just implemented is fractional cascading! A fraction of any array cascades up the rest of the arrays.
There is one more detail which has to be attended to. When I follow a pointer down, I might end up on an element which is not actually a member of the current array (it was one that was cascaded up). I need to be able to efficiently find the next element which is a member of the current array (and there might be many cascaded elements jammed between it and the next member element, so doing a left-scan could take a long time); so for every cascaded element I store a pointer to the predecessor member element.

Fractional cascading is a very useful transformation, used in a variety of contexts including layered range trees and 3D orthogonal range searching. In fact, it can be generalized in several ways. The first is that we can cascade some fixed fraction α of elements, rather than the 1/2 we did here. Additionally, we don’t have to limit ourselves to cascading up a list of arrays; we can cascade up an arbitrary graph, merging many lists together as long as we pick α to be less than 1/d, where d is the in-degree of the node.

Exercise. Previously, we described range trees. How can fractional cascading be used to reduce the query complexity by a factor of $O(\lg n)$?
Exercise. There is actually another way we can setup the pointers in a fractionally cascaded data structure. Rather than have downward pointers for every element, we only maintain pointers between elements which are identical (that is to say, they were cascaded up.) This turns out to be more convenient when you are constructing the data structure. However, you now need to maintain another set of pointers. What are they? (Hint: Consider the case where a search lands on a non-cascaded, member element.)
February 26, 2012Range trees are a data structure which lets you efficiently query a set of points and figure out what points are in some bounding box. They do so by maintaining nested trees: the first level is sorted on the x-coordinate, the second level on the y-coordinate, and so forth. Unfortunately, due to their fractal nature, range trees a bit hard to visualize. (In the higher dimensional case, this is definitely a “Yo dawg, I heard you liked trees, so I put a tree in your tree in your tree in your…”) But we’re going to attempt to visualize them anyway, by taking advantage of the fact that a sorted list is basically the same thing as a balanced binary search tree. (We’ll also limit ourselves to two-dimensional case for sanity’s sake.) I’ll also describe a nice algorithm for building range trees.
Suppose that we have a set of points $(x_1, y_1), (x_2, y_2), \cdots (x_n, y_n)$. How do we build a range tree? The first thing we do is build a balanced binary search tree for the x-coordinate (denoted in blue). There are a number of ways we can do this, including sorting the list with your favorite sorting algorithm and then building the BBST from that; however, we can build the tree directly by using quicksort with median-finding, pictured below left.

Once we’ve sorted on x-coordinate, we now need to re-sort every x-subtree on the y-coordinates (denoted in red), the results of which will be stored in another tree we’ll store inside the x-subtree. Now, we could sort each list from scratch, but since for any node we’re computing the y-sorted trees of its children, we can just merge them together ala mergesort, pictured above right. (This is where the -1 in $n\lg^{d-1} n$ comes from!)
So, when we create a range-tree, we first quicksort on the x-coordinate, and then mergesort on the y-coordinate (saving the intermediate results). This is pictured below:

We can interpret this diagram as a range tree as follows: the top-level tree is the x-coordinate BBST, as when we get the leaves we see that all of the points are sorted by x-coordinate. However, the points that are stored inside the intermediate nodes represent the y-coordinate BBSTs; each list is sorted on the y-coordinate, and implicitly represents another BBST. I’ve also thrown in a rendering of the points being held by this range tree at the bottom.
Let’s use this as our working example. If we want to find points between the x-coordinates 1 and 4 inclusive, we search for the leaf containing 1, the leaf containing 4, and take all of the subtrees between this.

What if we want to find points between the y-coordinates 2 and 4 inclusive, with no filtering on x, we can simply look at the BBST stored in the root node and do the range query.

Things are a little more interesting when we actually want to do a bounding box (e.g. (1,2) x (4,4) inclusive): first, we locate all of the subtrees in the x-BBST; then, we do range queries in each of the y-BBSTs.

Here is another example (4,4) x (7,7) inclusive. We get lucky this time and only need to check one y-BBST, because the X range directly corresponds to one subtree. In general, however, we will only need to check $O(\lg n)$ subtrees.

It should be easy to see that query time is $O(\lg^2 n)$ (since we may need to perform a 1-D range query on $O(\lg n)$ trees, and each query takes $O(\lg n)$ time). Perhaps less obviously, this scheme only takes up $O(n\lg n)$ space. Furthermore, we can actually get the query time down to $O(\lg n)$, using a trick called fractional cascading. But that’s for another post!















