A petri net is a curious little graphical modeling language for control flow in concurrency. They came up in this talk a few weeks ago: Petri-nets as an Intermediate Representation for Heterogeneous Architectures, but what I found interesting was how I could describe some common concurrency structures using this modeling language.
Here is, for example, the well venerated lock:
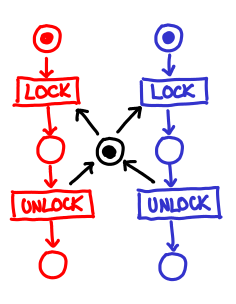
The way to interpret the graph is thus: each circle is a “petri dish” (place) that may contain some number of tokens. The square boxes (transitions) are actions that would like to fire, but in order to do so all of the petri dishes feeding into them must have tokens. It’s the sort of representation that you could make into a board game of sorts!
Read more...
To: Oliver Charles
Subject: [Haskell-cafe] Please review my Xapian foreign function interface
Thanks Oliver!
I haven’t had time to look at your bindings very closely, but I do have a few initial things to think about:
- You’re writing your imports by hand. Several other projects used to do this, and it’s a pain in the neck when you have hundreds of functions that you need to bind and you don’t quite do it all properly, and then you segfault because there was an API mismatch. Consider using a tool like c2hs which rules out this possibility (and reduces the code you need to write!)
- I see a lot of unsafePerformIO and no consideration for interruptibility or thread safety. People who use Haskell tend to expect their code to be thread-safe and interruptible, so we have high standards ;-) But even C++ code that looks thread safe may be mutating shared memory under the hood, so check carefully.
I use Sup, so I deal with Xapian on a day-to-day basis. Bindings are good to see.
Read more...
I spent some time fleshing out my count min sketch implementation for OCaml (to be the subject of another blog post), and along the way, I noticed a few more quirks about the OCaml language (from a Haskell viewpoint).
Unlike Haskell’s Int, which is 32-bit/64-bit, the built-in OCaml int type is only 31-bit/63-bit. Bit twiddlers beware! (There is a nativeint type which gives full machine precision, but it less efficient than the int type).
Read more...
I recently took the time out to rewrite the MVar documentation, which as it stands is fairly sparse (the introduction section rather tersely states “synchronising variables”; though to the credit of the original writers the inline documentation for the data type and its fundamental operations is fairly fleshed out.) I’ve reproduced my new introduction here.
While researching this documentation, I discovered something new about how MVars worked, which is encapsulated in this program. What does it do? :
Read more...
New to this series? Start at the beginning!.
Today we’re going to take a closer look at a somewhat unusual data type, Omega. In the process, we’ll discuss how the lub library works and how you might go about using it. This is of practical interest to lazy programmers, because lub is a great way to modularize laziness, in Conal’s words.
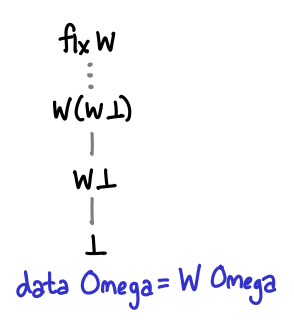
Omega is a lot like the natural numbers, but instead of an explicit Z (zero) constructor, we use bottom instead. Unsurprisingly, this makes the theory easier, but the practice harder (but not too much harder, thanks to Conal’s lub library). We’ll show how to implement addition, multiplication and factorial on this data type, and also show how to prove that subtraction and equality (even to vertical booleans) are uncomputable.
Read more...
Previously, we’ve drawn Hasse diagrams of all sorts of Haskell types, from data types to function types, and looked at the relationship between computability and monotonicity. In fact, all computable functions are monotonic, but not all monotonic functions are computable. Is there some description of functions that entails computability? Yes: Scott continuous functions. In this post, we look at the mathematical machinery necessary to define continuity. In particular, we will look at least upper bounds, chains, chain-complete partial orders (CPOs) and domains. We also look at fixpoints, which arise naturally from continuous functions.
Read more...
Between packing and hacking on GHC, I didn’t have enough time to cough up the next post of the series or edit the pictures for the previous post, so all you get today is a small errata post.
- The full list diagram is missing some orderings: ★:⊥ ≤ ★:⊥:⊥ and so on.
- In usual denotational semantics, you can’t distinguish between ⊥ and
λ_.⊥. However, as Anders Kaseorg and the Haskell Report point out, with seq you can distinguish them. This is perhaps the true reason why seq is a kind of nasty function. I’ve been assuming the stronger guarantee (which is what zygoloid pointed out) when it’s not actually true for Haskell. - The “ought to exist” arrow in the halts diagram goes the wrong direction.
- In the same fashion of the full list diagram,
head is missing some orderings, so in fact they gray blob is entirely connected. There are situations when we can have disconnected blobs, but not for a domain with only one maximum. - Obvious typo for fst.
- The formal partial order on functions was not defined correctly: it originally stated that for f ≤ g, f(x) = g(x); actually, it’s weaker than that: f(x) ≤ g(x).
- A non-erratum: the right-side of the head diagram is omitted because… adding all the arrows makes it look pretty ugly. Here is the sketch I did before I decided it wasn’t a good picture.

Read more...
Gin, because you’ll need it by the time you’re done reading this.
Last time we looked the partial orders of values for data types. There are two extra things I would like to add: an illustration of how star-subscript-bottom expands and an illustration of list without using the star-subscript-bottom notation.
Here is a triple of star-subscript-bottoms expanded, resulting in the familiar Hasse diagram of the powerset of a set of three elements ordered by inclusion:
Read more...
Values of Haskell types form a partial order. We can illustrate this partial order using what is called a Hasse diagram. These diagrams are quite good for forcing yourself to explicitly see the bottoms lurking in every type. Since my last post about denotational semantics failed to elicit much of a response at all, I decided that I would have better luck with some more pictures. After all, everyone loves pictures!
We’ll start off with something simple: () or unit.
Read more...
Ever try to go to haskell.org and notice that it was down? Well, now you have someone to complain to: the haskell.org committee has formed and apparently I’m on it. 8-)
One of the first things we’ll be doing is moving haskell.org from a server being hosted at Yale (the hosting has been good, but what will happen is the server will go down during the weekend and there will be no one to kick it until Monday) to some dedicated hardware. I must admit, I do feel a bit sheepish for being on the committee but not having any bits (or direct experience) to help do the maintenance work—hopefully that will change soon.
Read more...


