Some notes collected from a close read of Conal Elliot’s Compiling to Categories and The Simple Essence of Automatic Differentiation.
A colleague of mine was trying to define a “tree structure” of tensors, with the hope of thereby generalizing the concept to also work with tensors that have “ragged dimensions.” Let’s take a look:
Suppose we have a (2, 3) matrix:
tensor([[1, 2, 3],
[4, 5, 6]])
One way to think about this is that we have a “tree” of some sort, where the root of the tree branches to two subnodes, and then each subnode branches to three nodes:
Read more...
New to this series? Start at the beginning!
Recursion is perhaps one of the first concepts you learn about when you learn functional programming (or, indeed, computer science, one hopes.) The classic example introduced is factorial:
fact :: Int -> Int
fact 0 = 1 -- base case
fact n = n * fact (pred n) -- recursive case
Recursion on natural numbers is closely related to induction on natural numbers, as is explained here.
Read more...
New to this series? Start at the beginning!.
Today we’re going to take a closer look at a somewhat unusual data type, Omega. In the process, we’ll discuss how the lub library works and how you might go about using it. This is of practical interest to lazy programmers, because lub is a great way to modularize laziness, in Conal’s words.
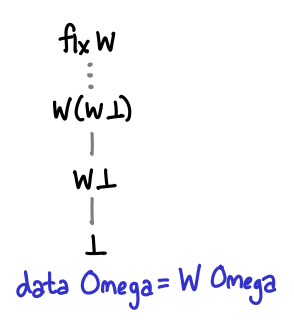
Omega is a lot like the natural numbers, but instead of an explicit Z (zero) constructor, we use bottom instead. Unsurprisingly, this makes the theory easier, but the practice harder (but not too much harder, thanks to Conal’s lub library). We’ll show how to implement addition, multiplication and factorial on this data type, and also show how to prove that subtraction and equality (even to vertical booleans) are uncomputable.
Read more...
Previously, we’ve drawn Hasse diagrams of all sorts of Haskell types, from data types to function types, and looked at the relationship between computability and monotonicity. In fact, all computable functions are monotonic, but not all monotonic functions are computable. Is there some description of functions that entails computability? Yes: Scott continuous functions. In this post, we look at the mathematical machinery necessary to define continuity. In particular, we will look at least upper bounds, chains, chain-complete partial orders (CPOs) and domains. We also look at fixpoints, which arise naturally from continuous functions.
Read more...
Between packing and hacking on GHC, I didn’t have enough time to cough up the next post of the series or edit the pictures for the previous post, so all you get today is a small errata post.
- The full list diagram is missing some orderings: ★:⊥ ≤ ★:⊥:⊥ and so on.
- In usual denotational semantics, you can’t distinguish between ⊥ and
λ_.⊥. However, as Anders Kaseorg and the Haskell Report point out, with seq you can distinguish them. This is perhaps the true reason why seq is a kind of nasty function. I’ve been assuming the stronger guarantee (which is what zygoloid pointed out) when it’s not actually true for Haskell. - The “ought to exist” arrow in the halts diagram goes the wrong direction.
- In the same fashion of the full list diagram,
head is missing some orderings, so in fact they gray blob is entirely connected. There are situations when we can have disconnected blobs, but not for a domain with only one maximum. - Obvious typo for fst.
- The formal partial order on functions was not defined correctly: it originally stated that for f ≤ g, f(x) = g(x); actually, it’s weaker than that: f(x) ≤ g(x).
- A non-erratum: the right-side of the head diagram is omitted because… adding all the arrows makes it look pretty ugly. Here is the sketch I did before I decided it wasn’t a good picture.

Read more...
Gin, because you’ll need it by the time you’re done reading this.
Last time we looked the partial orders of values for data types. There are two extra things I would like to add: an illustration of how star-subscript-bottom expands and an illustration of list without using the star-subscript-bottom notation.
Here is a triple of star-subscript-bottoms expanded, resulting in the familiar Hasse diagram of the powerset of a set of three elements ordered by inclusion:
Read more...
Values of Haskell types form a partial order. We can illustrate this partial order using what is called a Hasse diagram. These diagrams are quite good for forcing yourself to explicitly see the bottoms lurking in every type. Since my last post about denotational semantics failed to elicit much of a response at all, I decided that I would have better luck with some more pictures. After all, everyone loves pictures!
We’ll start off with something simple: () or unit.
Read more...
An extended analogy on the denotational and game semantics of ⊥
This is an attempt at improving on the Haskell Wikibooks article on Denotational Semantics by means of a Dr. Strangelove inspired analogy.
The analogy. In order to prevent Brigadier General Jack D. Ripper from initiating a nuclear attack on Russia, the Pentagon decides that it will be best if every nuclear weapon requires two separate keys in order to be activated, both of which should not be known by the same person at the same time under normal circumstances. Alice is given one half of the key, Bob the other half. If Ripper asks Alice for her half of the key, she can tell him her key, A. However, asking Alice for Bob’s key won’t work, since she doesn’t know what Bob’s key is.
Read more...

