ezyang's blog

Visualizing satisfiability, validity & entailment

So you’re half bored to death working on your propositional logic problem set (after all, you know what AND and OR are, being a computer scientist), and suddenly the problem set gives you a real stinker of a question:

Is it true that Γ ⊢ A implies that Γ ⊢ ¬A is false?

and you think, “Double negation, no problem!” and say “Of course!” Which, of course, is wrong: right after you turn it in, you think, “Aw crap, if Γ contains a contradiction, then I can prove both A and ¬A.” And then you wonder, “Well crap, I have no intuition for this shit at all.”

Actually, you probably already have a fine intuition for this sort of question, you just don’t know it yet.

The first thing we want to do is establish a visual language for sentences of propositional logic. When we talk about a propositional sentence such as A ∨ B, there are some number of propositional variables which need assignments given to them, e.g. A is true, B is false. We can think of these assignments as forming a set of size 2^n, where n is the number of propositional variables being considered. If n were small, we could simply draw a Venn diagram, but since n could be quite big we’ll just visualize it as a circle:

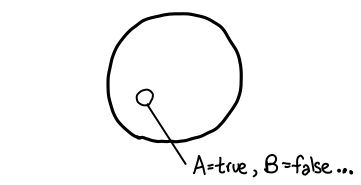
We’re interested in subsets of assignments. There are lots of ways to define these subsets; for example, we might consider the set of assignments where A is assigned to be true. But we’ll be interested in one particular type of subset: in particular, the subset of assignments which make some propositional sentence true. For example, “A ∨ B” corresponds to the set {A=true B=true, A=true B=false, A=false B=true}. We’ll draw a subset graphically like this:

Logical connectives correspond directly to set operations: in particular, conjunction (AND ∧) corresponds to set intersection (∩) and disjunction (OR ∨) corresponds to set union (∪). Notice how the corresponding operators look very similar: this is not by accident! (When I was first learning my logical operators, this is how I kept them straight: U is for union, and it all falls out from there.)

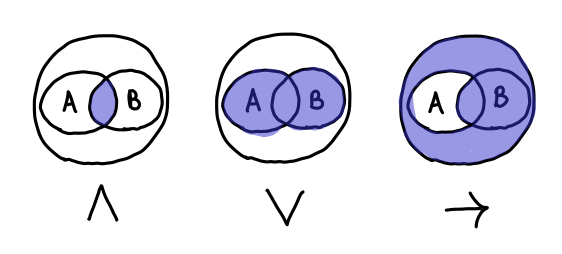
Now we can get to the meat of the matter: statements such as unsatisfiability, satisfiability and validity (or tautology) are simply statements about the shape of these subsets. We can represent each of these visually: they correspond to empty, non-empty and complete subsets respectively:

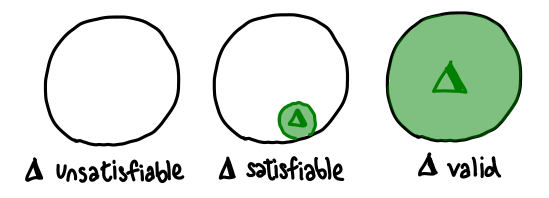
This is all quite nice, but we haven’t talked about how the turnstile (⊢) aka logical entailment fits into the picture. In fact, when I say something like “B ∨ ¬B is valid”, what I’m actually saying is “⊢ B ∨ ¬B is true”; that is to say, I can always prove “B ∨ ¬B”, no matter what hypothesis I am permitted.”

So the big question is this: what happens when I add some hypotheses to the mix? If we think about what is happening here, when I add a hypothesis, I make life “easier” for myself in some sense: the more hypotheses I add, the more propositional sentences are true. To flip it on its head, the more hypotheses I add, the smaller the space of assignments I have to worry about:

All I need for Γ ⊢ φ to be true is for all of the assignments in Γ to cause φ to be true, i.e. Γ must be contained within φ.

Sweet! So let’s look at this question again:

Is it true that Γ ⊢ A implies that Γ ⊢ ¬A is false?

Recast as a set theory question, this is:

For all Γ and A, is it true that Γ ⊂ A implies that Γ ⊄ A^c? (set complement)

We consider this for a little bit, and realize: “No! For it is true that the empty set is a subset of all sets!” And of course, the empty set is precisely a contradiction: subset of everything (ex falso), and superset of nothing but itself (only contradiction implies contradiction).

It turns out that Γ is a set as well, and one may be tempted to ask whether or not set operations on Γ have any relationship to the set operations in our set-theoretic model. It is quite tempting, because unioning together Γ seems to work quite well: Γ ∪ Δ seems to give us the conjunction of Γ and Δ (if we interpret the sets by ANDing all of their elements together.) But in the end, the best answer to give is “No”. In particular, set intersection on Γ is incoherent: what should {A} ∩ {A ∧ A} be? A strictly syntactic comparison would say {}, even though clearly A ∧ A = A. Really, the right thing to do here is to perform a disjunction, but this requires us to say {A} ∩ {B} = {A ∨ B}, which is confusing and better left out of sight and out of mind.