Visualizing range trees
Range trees are a data structure which lets you efficiently query a set of points and figure out what points are in some bounding box. They do so by maintaining nested trees: the first level is sorted on the x-coordinate, the second level on the y-coordinate, and so forth. Unfortunately, due to their fractal nature, range trees a bit hard to visualize. (In the higher dimensional case, this is definitely a “Yo dawg, I heard you liked trees, so I put a tree in your tree in your tree in your...”) But we’re going to attempt to visualize them anyway, by taking advantage of the fact that a sorted list is basically the same thing as a balanced binary search tree. (We’ll also limit ourselves to two-dimensional case for sanity’s sake.) I’ll also describe a nice algorithm for building range trees.
Suppose that we have a set of points . How do we build a range tree? The first thing we do is build a balanced binary search tree for the x-coordinate (denoted in blue). There are a number of ways we can do this, including sorting the list with your favorite sorting algorithm and then building the BBST from that; however, we can build the tree directly by using quicksort with median-finding, pictured below left.
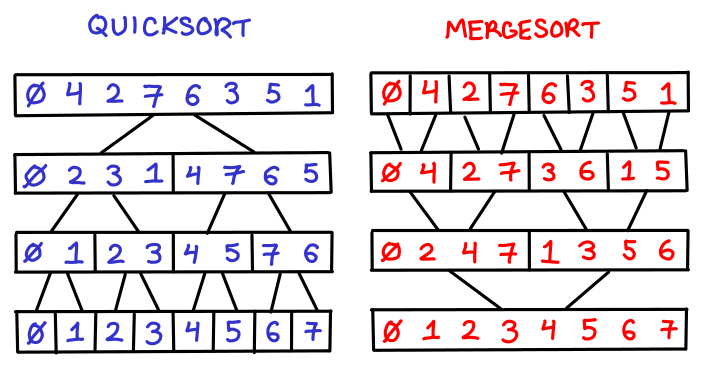
Once we’ve sorted on x-coordinate, we now need to re-sort every x-subtree on the y-coordinates (denoted in red), the results of which will be stored in another tree we’ll store inside the x-subtree. Now, we could sort each list from scratch, but since for any node we're computing the y-sorted trees of its children, we can just merge them together ala mergesort, pictured above right. (This is where the -1 in comes from!)
So, when we create a range-tree, we first quicksort on the x-coordinate, and then mergesort on the y-coordinate (saving the intermediate results). This is pictured below:
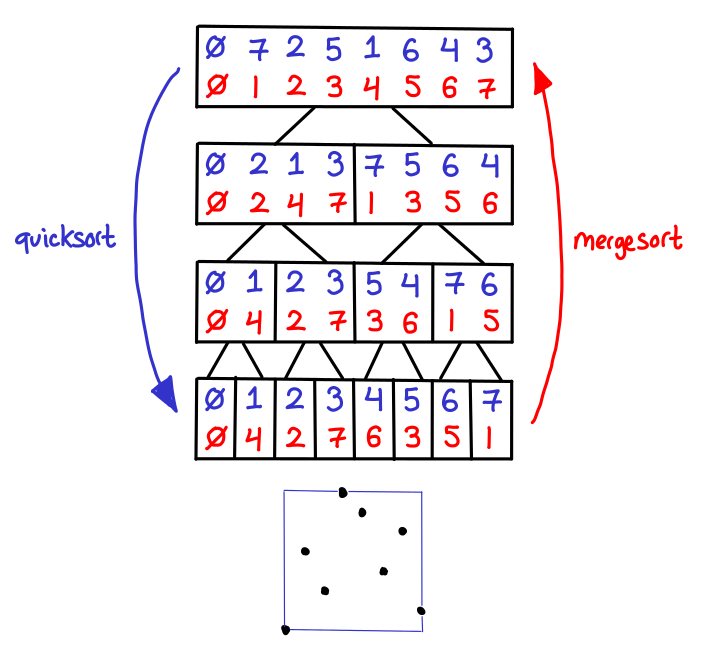
We can interpret this diagram as a range tree as follows: the top-level tree is the x-coordinate BBST, as when we get the leaves we see that all of the points are sorted by x-coordinate. However, the points that are stored inside the intermediate nodes represent the y-coordinate BBSTs; each list is sorted on the y-coordinate, and implicitly represents another BBST. I’ve also thrown in a rendering of the points being held by this range tree at the bottom.
Let’s use this as our working example. If we want to find points between the x-coordinates 1 and 4 inclusive, we search for the leaf containing 1, the leaf containing 4, and take all of the subtrees between this.

What if we want to find points between the y-coordinates 2 and 4 inclusive, with no filtering on x, we can simply look at the BBST stored in the root node and do the range query.
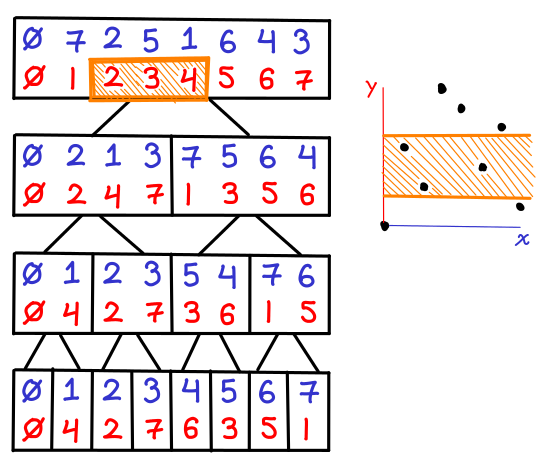
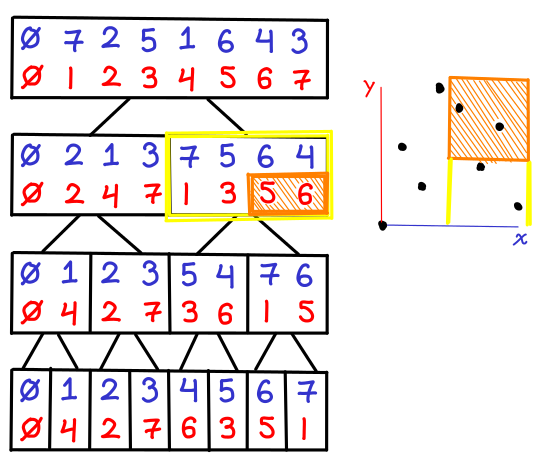
Things are a little more interesting when we actually want to do a bounding box (e.g. (1,2) x (4,4) inclusive): first, we locate all of the subtrees in the x-BBST; then, we do range queries in each of the y-BBSTs.
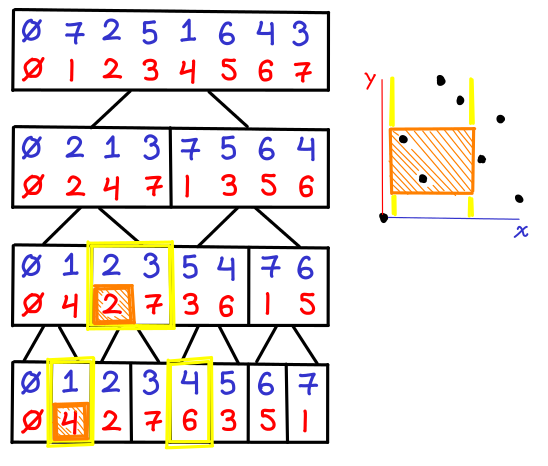
Here is another example (4,4) x (7,7) inclusive. We get lucky this time and only need to check one y-BBST, because the X range directly corresponds to one subtree. In general, however, we will only need to check subtrees.
It should be easy to see that query time is (since we may need to perform a 1-D range query on
trees, and each query takes
time). Perhaps less obviously, this scheme only takes up
space. Furthermore, we can actually get the query time down to
, using a trick called fractional cascading. But that’s for another post!