ezyang’s blog

I recently encountered the following pattern while writing some Haskell code, and was surprised to find there was not really any support for it in the standard libraries. I don’t know what it’s called (neither did Simon Peyton-Jones, when I mentioned it to him), so if someone does know, please shout out. The pattern is this: many times an endomorphic map (the map function is a -> a) will not make very many changes to the underlying data structure. If we implement the map straight-forwardly, we will have to reconstruct the entire spine of the recursive data structure. However, if we use instead the function a -> Maybe a, we can reuse old pieces of the map if there were no changes to it. (Regular readers of my blog may recognize this situation from this post.) So what is such an alternative map (a -> Maybe a) -> f a -> Maybe (f a) called?

One guess it might be the traverse function in Data.Traversable: it certainly has a very similar type signature: Applicative f => (a -> f b) -> t a -> f (t b). However, the semantics are subtly different, as you can see from this example:

Data.Traversable> traverse (\x -> if x == 2 then Just 3 else Nothing) [1,2,3]
Nothing

Recall that our function only returns Nothing in the event of no change. Thus, we should have gotten the result Just [1,3,3]: the first and third elements of the list unchanged, and the second element of the list with its new value.

How would we implement such a function for lists? Here’s a simple implementation:

nonSharingMap :: (a -> Maybe a) -> [a] -> Maybe [a]
nonSharingMap f xs = let (b, r) = foldr g (False, []) (zip xs (map f xs))
                     in if b then Just r else Nothing
    where g (y, Nothing) (b, ys) = (b,     y:ys)
          g (_, Just y)  (_, ys) = (True,  y:ys)

But we can do better than this. Consider a situation where all elements of the list except the head stay the same:

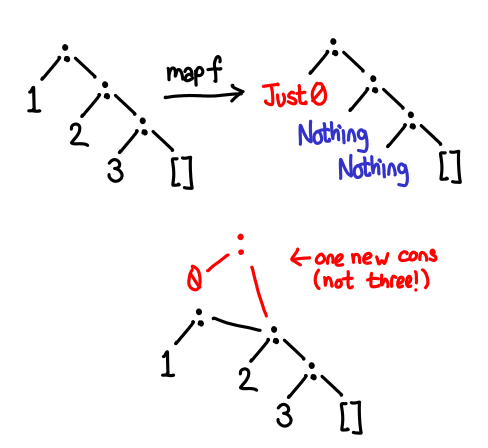
We would like to share the tail of the list between the old and new versions. With a little head-scratching, and the realization that tails shares, we can write this version:

sharingMap :: (a -> Maybe a) -> [a] -> Maybe [a]
sharingMap f xs = let (b, r) = foldr g (False, []) (zip3 (tails xs) xs (map f xs))
                     in if b then Just r else Nothing
    where g (_,   y, Nothing) (True, ys)  = (True,  y:ys)
          g (_,   _, Just y)  (True, ys)  = (True,  y:ys)
          g (ys', _, Nothing) (False, _)  = (False, ys')
          g (_,   _, Just y)  (False, ys) = (True,  y:ys)

Open questions: what is this pattern called? Why doesn’t it follow the usual applicative structure? Does it fulfill some higher order pattern? Also, this scheme isn’t fully compositional: if I pass you a Nothing, you have no access to the original version in case there was a change elsewhere in the structure: (Bool, a) might be a little more compositional. Does this mean this is an example of the state monad? What about sharing?

Update. Anders Kaseorg writes in with a much more straight-forward, directly recursive version of the function:

sharingMap f [] = Nothing
sharingMap f (x : xs) = case (f x, sharingMap f xs) of
  (Nothing, Nothing) -> Nothing
  (y, ys) -> Just (fromMaybe x y : fromMaybe xs ys)

I haven't checked, but one hope of expressing the function in terms of foldr and zip3 is that one may be able to get it to fuse. Of course, for actual recursive spine-strict data types, you usually won't be able to fuse, and so a more straightforward presentation is more normal.