Type Technology Tree
They say that one doesn’t discover advanced type system extensions: rather, the type system extensions discover you! Nevertheless, it’s worthwhile to know what the tech tree for GHC’s type extensions are, so you can decide how much power (and the correspondingly headache inducing error messages) you need. I’ve organized the relations in the following diagram with the following criterion in mind:
- Some extensions automatically enable other extensions (implies);
- Some extensions offer all the features another extension offers (subsumes);
- Some extensions work really nicely with other extensions (synergy);
- Some extensions offer equivalent (but differently formulated) functionality to another extension (equiv).
It’s also worth noting that the GHC manual divides these extensions into “Extensions to data types and type synonyms”, “Class and instances declarations”, “Type families” and “Other type system extensions”. I have them organized here a little differently.
Rank and data
Our first tech tree brings together two extensions: arbitrary-rank polymorphism and generalized algebraic data types.
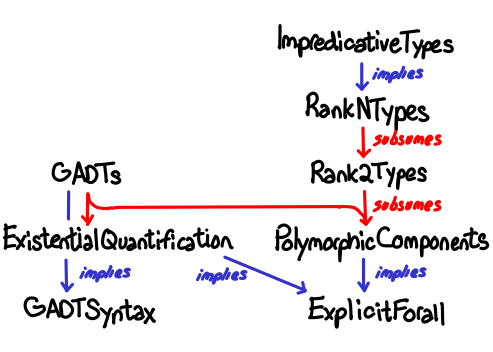
Briefly:
- GADTSyntax permits ordinary data types to be written GADT-style (with explicit constructor signatures): data C where C :: Int -> C
- ExplicitForall allows you to explicitly state the quantifiers in polymorphic types: forall a. a -> a
- ExistentialQuantification allows types to be hidden inside a data constructor: data C = forall e. C e
- GADTs permits explicit constructor signatures: data C where C :: C a -> C b -> C (a, b). Subsumes ExistentialQuantification because existentially quantified data types are simply polymorphic constructors for which the type variable isn’t in the result.
- PolymorphicComponents allows you to write forall inside data type fields: data C = C (forall a. a)
- Rank2Types allows polymorphic arguments: f :: (forall a. a -> a) -> Int -> Int. This with GADTs subsumes PolymorphicComponents because data type fields with forall within them correspond to data constructors with rank-2 types.
- RankNTypes: f :: Int -> (forall a. a -> a)
- ImpredicativeTypes allows polymorphic functions and data structures to be parametrized over polymorphic types: Maybe (forall a. a -> a)
Instances
Our next tech tree deals with type class instances.
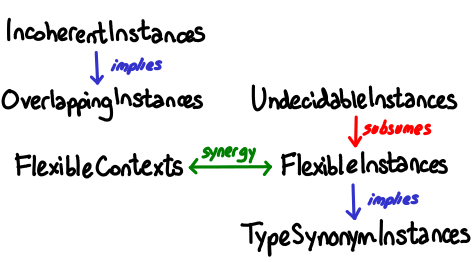
Briefly:
- TypeSynonymInstances permits macro-like usage of type synonyms in instance declarations: instance X String
- FlexibleInstances allows more instances for more interesting type expressions, with restrictions to preserve decidability: instance MArray (STArray s) e (ST s) (frequently seen with multi-parameter type classes, which are not in the diagram)
- UndecidableInstances allows instances for more interesting type expression with no restrictions, at the cost of decidability. See Oleg for a legitimate example.
- FlexibleContexts allows more type expressions in constraints of functions and instance declarations: g :: (C [a], D (a -> b)) => [a] -> b
- OverlappingInstances allows instances to overlap if there is a most specific one: instance C a; instance C Int
- IncoherentInstances allows instances to overlap arbitrarily.
Perhaps conspicuously missing from this diagram is MultiParamTypeClasses which is below.
Type families and functional dependencies
Our final tech tree addresses programming with types:
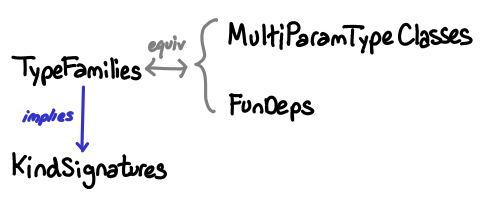
Briefly:
- KindSignatures permits stating the kind of a type variable: m :: * -> *
- MultiParamTypeClasses allow type classes to range over multiple type variables: class C a b
- FunDeps allow restricting instances of multi-parameter type classes, helping resolve ambiguity: class C a b | a -> b
- TypeFamilies allow “functions” on types: data family Array e
The correspondence between functional dependencies and type families is well known, though not perfect (type families can be more wordy and can’t express certain equalities, but play more nicely with GADTs).