ezyang’s blog

A petri net is a curious little graphical modeling language for control flow in concurrency. They came up in this talk a few weeks ago: Petri-nets as an Intermediate Representation for Heterogeneous Architectures, but what I found interesting was how I could describe some common concurrency structures using this modeling language.

Here is, for example, the well venerated lock:

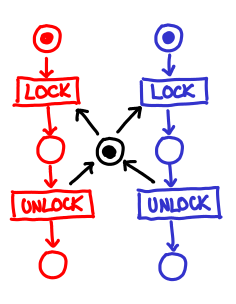
The way to interpret the graph is thus: each circle is a “petri dish” (place) that may contain some number of tokens. The square boxes (transitions) are actions that would like to fire, but in order to do so all of the petri dishes feeding into them must have tokens. It’s the sort of representation that you could make into a board game of sorts!

If multiple transitions can fire off, we pick one of them and only that one succeeds; the ability for a token to flow down one or another arrow encodes nondeterminism in this model. In the lock diagram, only one branch can grab the lock token in the middle, but they return it once they exit the critical area (unlock).

Here is a semaphore:

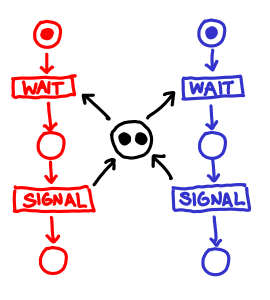
It’s exactly the same, except that the middle place may contain more than one token. Of course, no one said that separate processes must wait before signalling. We can implement a simple producer-consumer chain like this:

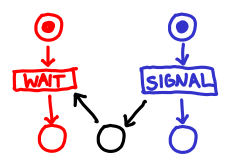
Note that petri net places are analogous to MVar (), though it takes a little care to ensure we are not manufacturing tokens out of thin air in Haskell, due to the lack of linear types. You may also notice that petri nets say little about data flow; we can imagine the tokens as data, but the formalism doesn’t say much about what the tokens actually represent.