High performance monads
Continuations are well known for being notoriously tricky to use: they are the “gotos” of the functional programming world. They can make a mess or do amazing things (after all, what are exceptions but a well structured nonlocal goto). This post is intended for readers with a passing familiarity with continuations but a disbelief that they could be useful for their day-to-day programming tasks: I’d like to show how continuations let us define high performance monads ala the Logic monad in a fairly methodical way. A (possibly) related post is The Mother of all Monads.
> import Prelude hiding (Maybe(..), maybe)
We’ll start off with a warmup: the identity monad.
> data Id a = Id a > instance Monad Id where > Id x >>= f = f x > return = Id
The continuation-passing style (CPS) version of this monad is your stock Cont monad, but without callCC defined.
> data IdCPS r a = IdCPS { runIdCPS :: (a -> r) -> r }
> instance Monad (IdCPS r) where
> IdCPS c >>= f =
> IdCPS (\k -> c (\a -> runIdCPS (f a) k))
> return x = IdCPS (\k -> k x)
While explaining CPS is out of the scope of this post, I’d like to point out a few idioms in this translation that we’ll be reusing for some of the more advanced monads.
- In order to “extract” the value of c, we pass it a lambda (\a -> ...), where a is the result of the c computation.
- There is only one success continuation k :: a -> r, which is always eventually used. In the case of bind, it’s passed to runIdCPS, in the case of return, it’s directly invoked. In later monads, we’ll have more continuations floating around.
Following in step with monad tutorials, the next step is to look at the venerable Maybe data type, and its associated monad instance.
> data Maybe a = Nothing | Just a > instance Monad Maybe where > Just x >>= f = f x > Nothing >>= f = Nothing > return = Just
When implementing the CPS version of this monad, we’ll need two continuations: a success continuation (sk) and a failure continuation (fk).
> newtype MaybeCPS r a = MaybeCPS { runMaybeCPS :: (a -> r) -> r -> r }
> instance Monad (MaybeCPS r) where
> MaybeCPS c >>= f =
> MaybeCPS (\sk fk -> c (\a -> runMaybeCPS (f a) sk fk) fk)
> return x = MaybeCPS (\sk fk -> sk x)
Compare this monad with IdCPS: you should notice that it’s quite similar. In fact, if we eliminated all mention of fk from the code, it would be identical! Our monad instance heartily endorses success. But if we add the following function, things change:
> nothingCPS = MaybeCPS (\_ fk -> fk)
This function ignores the success continuation and invokes the failure continuation: you should convince yourself that one it invokes the failure continuation, it immediately bugs out of the MaybeCPS computation. (Hint: look at any case we run a MaybeCPS continuation: what do we pass in for the failure continuation? What do we pass in for the success continuation?)
For good measure, we could also define:
> justCPS x = MaybeCPS (\sk _ -> sk x)
Which is actually just return in disguise.
You might also notice that the signature of our MaybeCPS newtype strongly resembles the signature of the maybe “destructor” function—thus called because it destroys the data structure:
> maybe :: Maybe a -> (a -> r) -> r -> r > maybe m sk fk = > case m of > Just a -> sk a > Nothing -> fk
(The types have been reordered for pedagogical purposes.) I’ve deliberately named the “default value” fk: they are the same thing!
> monadicAddition mx my = do > x <- mx > y <- my > return (x + y) > maybeTest = maybe (monadicAddition (Just 2) Nothing) print (return ()) > maybeCPSTest = runMaybeCPS (monadicAddition (return 2) nothingCPS) print (return ())
Both of these pieces of code have the same end result. However, maybeTest constructs a Maybe data structure inside the monadic portion, before tearing it down again. runMaybeCPS skips this process entirely: this is where the CPS transformation derives its performance benefit: there’s no building up and breaking down of data structures.
Now, to be fair to the original Maybe monad, in many cases GHC will do this transformation for you. Because algebraic data types encourage the creation of lots of little data structures, GHC will try its best to figure out when a data structure is created and then immediately destructed, and optimize out that wasteful behavior. Onwards!
The list monad (also known as the “stream” monad) encodes nondeterminism.
> data List a = Nil | Cons a (List a) > instance Monad List where > Nil >>= _ = Nil > Cons x xs >>= f = append (f x) (xs >>= f) > return x = Cons x Nil > append Nil ys = ys > append (Cons x xs) ys = Cons x (append xs ys)
Nil is essentially equivalent to Nothing, so our friend the failure continuation comes back to the fray. We have to treat our success continuation a little differently though: while we could just pass it the value of the first Cons of the list, this wouldn’t let us ever get past the first item of the list. So we’ll need to pass our success continuation a resume continuation (rk) in case it wants to continue down its path.
> newtype LogicCPS r a = LogicCPS { runLogicCPS :: (a -> r -> r) -> r -> r }
> instance Monad (LogicCPS r) where
> LogicCPS c >>= f =
> LogicCPS (\sk fk -> c (\a rk -> runLogicCPS (f a) sk rk) fk)
> return x = LogicCPS (\sk fk -> sk x fk)
Remember that return generates singleton lists, so there’s nothing more to continue on to, and we give the success continuation fk as the resume continuation.
The old data constructors also can be CPS transformed: nilCPS looks just like nothingCPS. consCPS invokes the success continuation, and needs to generate a resume continuation, which conveniently enough is given by its second argument:
> nilCPS = > LogicCPS (\_ fk -> fk) > consCPS x (LogicCPS c) = > LogicCPS (\sk fk -> sk x (c sk fk)) > appendCPS (LogicCPS cl) (LogicCPS cr) = > LogicCPS (\sk fk -> cl sk (cr sk fk))
These types should be looking awfully familiar. Rearranging this type a little (and renaming b→r):
foldr :: (a -> b -> b) -> b -> [a] -> b
I get:
fold :: List a -> (a -> r -> r) -> r -> r
Hey, that’s my continuation. So all we’ve done is a fold, just without actually constructing the list!
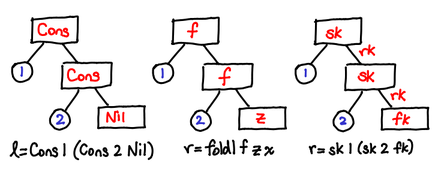
Keen readers will have also noticed that the CPS formulation of the list is merely the higher-order Church encoding of lists.
The CPS transformed version of the list monad wins big in several ways: we never need to construct and destruct the list and appending two lists takes O(1) time.
One last example: the leafy tree monad (cribbed from Edward Kmett’s finger tree slides):
> data Leafy a = Leaf a | Fork (Leafy a) (Leafy a) > instance Monad Leafy where > Leaf a >>= f = f a > Fork l r >>= f = Fork (l >>= f) (r >>= f) > return a = Leaf a
As it turns out, if we want to fold over this data type, we can reuse LogicCPS:
> leafCPS x = return x > forkCPS l r = appendCPS l r
To go in the other direction, if we combine all of the CPS operations on logic we’ve defined thus far and turn them back into a data type, we get a catenable list:
> data Catenable a = Append (Catenable a) (Catenable a) | List (List a)
To wrap (fold) up, we’ve shown that when we build up a large data structure that is only going to be destructed when we’re done, we’re better off fusing the two processes together and turn our data structure back into code. Similarly, if we would like to do “data structure”-like things to our data structure, it is probably better to actually build it up: the Church encodings for things like tail are notoriously inefficient. I’ve not said anything about monads that encode state of some sort: in many ways they’re a different breed of monad from the control flow monad (perhaps a more accurate statement is “Cont is the mother of all control flow monads”).
To quote Star Wars, the next time you find yourself entangled in a mess of continuations, use the data structure!
Addendum. CPS transforming data structure traversal has nothing to do with monads. You can do it to anything. It just so happens that the killer feature of control flow monads, nondeterminism, happens to really benefit from this transformation.
References. There are loads and loads of existing treatments of this subject.
- haskell.org wiki mentions CPS transforming monads for performance,
- This mailing list thread seems to imply that CPS transformation can make code slower, but in fact, they never ditch the construction of their data type.
- Representing variant types uniformly via executable code has a long and proud tradition under the term tagless. Some of them include Oleg’s treatment for embedded languages and the GHC developer’s Spineless Tagless G-machine under the hood.
- This ICFP presentation notes the similarity between the stream monad and the backtracking logic monad, and unifies the two with the moral equivalent of a fold.
I’ve probably missed a bunch of other obvious ones too.